在卷积网络搭建过程中，遇到了一个困惑，那就是如何根据卷积的一些超参数来计算网络的输出的大小，即卷积尺寸变化

为了使得计算过程更加直观，定义以下参数

定义

定义  

定义

输入尺寸为

输出尺寸为

则有卷积尺寸变化为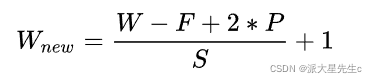 

例如，输入为28  ，卷积核为3*3  ，步长stride=1，padding=1，由以上公式可以得出新的输出为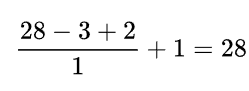

输出任然为28不变

但是肯定会有不能被整除的状况，在PyTorch中可以看到

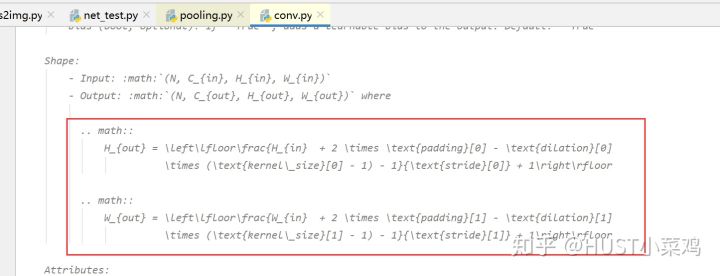
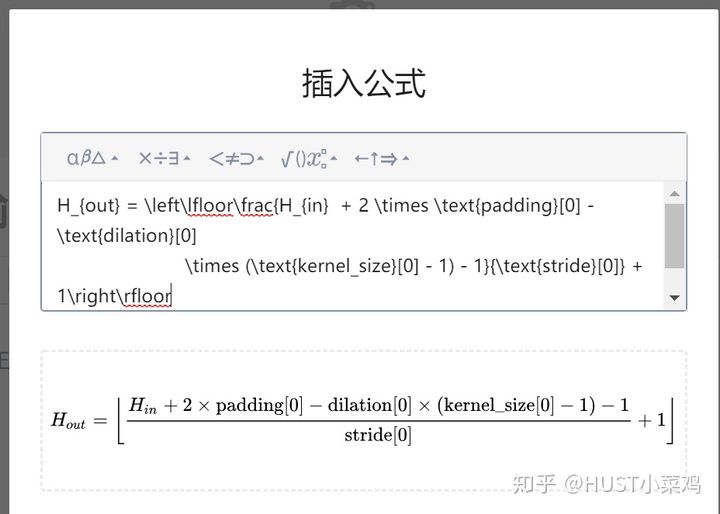
池化类似

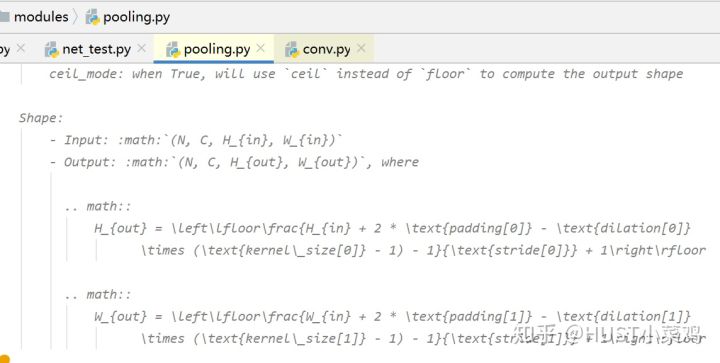
Shape:
        - Input: :math:`(N, C, H_{in}, W_{in})`
        - Output: :math:`(N, C, H_{out}, W_{out})`, where

          .. math::
              H_{out} = \left\lfloor\frac{H_{in} + 2 * \text{padding[0]} - \text{dilation[0]}
                    \times (\text{kernel\_size[0]} - 1) - 1}{\text{stride[0]}} + 1\right\rfloor

          .. math::
              W_{out} = \left\lfloor\frac{W_{in} + 2 * \text{padding[1]} - \text{dilation[1]}
                    \times (\text{kernel\_size[1]} - 1) - 1}{\text{stride[1]}} + 1\right\rfloor

在PyTorch中对于不能整除的状况默认均为向下取整，可以选择向上取整