写在前面：这个是我自己学习数据库系统概论写的笔记，大部分都是学习的时候有不懂的用AI问答搞明白之后再整理总结出来的知识点，供以后复习以及需要的小伙伴学习。如果有错的还请大家指正，祝大家都能学习进步！

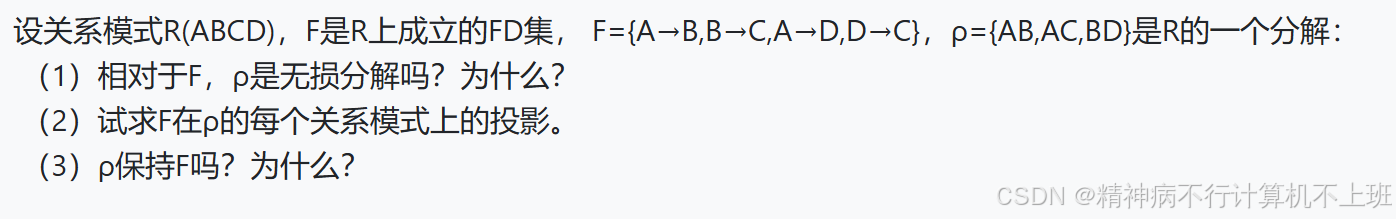
注：AB指的是包含A列和B列的一个子表，换句话说，就是你从原始的大表中抽取出这两列数据组成的新表。AC,BD同理。

1. ρ是什么？

在数据库中，假设你有一个表（关系模式），里面有很多列（比如 A, B, C, D）。然后，你决定把这个表分成几个小表。这个过程就叫做分解。你分解后的这些小表就是我们说的ρ（这里的 ρ是表示分解的符号）。

例如，你把原始的表 R(ABCD)分成三个小表：

• AB（包含 A和B）
• AC（包含A和C）
• BD（包含B和D）

这些小表就是 ρ={AB,AC,BD}。

2. 什么是无损连接？

无损连接的意思是，当你把这些小表重新合并（连接）回原来的大表时，不会丢失任何信息。

简单来说，就是：

• 你分拆表格的时候，数据没有丢失；
• 你能从小表中恢复出完整的原始大表。

3. 如何判断分解是不是无损连接？

1.无损连接的条件

为了确保分解是无损连接的，我们需要满足这样一个条件：

• 对于每一对小表（例如AB和AC），它们的交集应该至少包含候选键。这里的候选键是A（因为从A 就可以推导出其他所有列）。

2.具体检查：

• 看看每一对小表之间有哪些列是相同的（这叫做它们的“交集”）。
• 如果交集里面有候选码的列（在这里是 A），那么这个分解就是无损连接的。

3.具体到你的分解：

• AB和AC这两个小表有共同的列A（这是候选键）。AB和 AC共享A，这就说明我们通过A可以将这两个小表重新合并成原来的数据，保持信息不丢失。即它们有共同的列A，并且A 是候选键。所以它们的交集满足无损连接条件。
• AB和BD这两个小表有共同的列B。AB和BD共享B，但没有直接涉及到候选键A，这不是很关键。它们有共同的列B，但是B 不是候选键。所以，这两个小表的交集不能保证无损连接。
• AC和BD这两个小表没有共同的列。AC和BD之间没有任何共享的列，所以它们的交集是空的。它们没有共同的列，所以它们的交集是空的，也不能保证无损连接。
• 所以：这个分解不满足无损连接条件，因为AB和BD的交集只是列B，而B 不是候选键，而且AC和BD完全没有共同列。所以这个分解不是无损连接的。

只要交集里面有一个候选键（这里是A），我们就能保证合并后不会丢失数据。所以这个分解是 无损连接。

4. 什么是投影？

1.定义：

在数据库中，投影是指将一个关系模式上的函数依赖（FDs）“映射”到它的子集上，也就是“筛选”出在某个小表中依然成立的函数依赖。

2.例如：

假设你有一个大的关系模式 R(ABCD)，并且这个关系模式上有一些函数依赖

F={A→B,B→C,A→D,D→C}。

当你把关系模式R分解成几个小表 AB,AC,BD时，我们需要计算每个小表上仍然有效的函数依赖（也就是投影）。这些投影就是你在这些小表中能“保持”的函数依赖。

3.如何求投影：

我们逐个计算每个小表上的投影。对于每个小表，我们会把原始的函数依赖集F中那些包含小表列的函数依赖保留下来，其他的就被丢掉。

5. 投影在分解中的作用：

投影的作用是让我们从原始的函数依赖（FD）集中提取出每个小表的“投影”函数依赖。

也就是说，给定的分解会影响原始的函数依赖集 F={A→B,B→C,A→D,D→C}。我们需要为每个小表计算出它自己的函数依赖集。

比如：

• AB这个小表只涉及到A和B，那么 A→B会是它的投影依赖。
• AC这个小表只涉及到A和C，那么 A→C会是它的投影依赖。

这样就能得到每个小表的“投影”依赖关系。

6.“ρ保持F吗？”

1.如何理解“ρ保持F吗？”：

这句话的意思是：分解后的小表（即ρ中的每个小表）能否保持原始的函数依赖集 F，也就是说，在分解后的各个小表上，原始的函数依赖是否仍然成立。

2.具体解释：

• 我们有一个原始的关系模式 R(ABCD)，和一个函数依赖集F，它包含了一些属性之间的依赖关系。
• 然后，我们将关系模式R分解成了多个小表（这里是 ρ={AB,AC,BD}。
• 问题是：在这些小表中，原来关系模式R上的函数依赖（也就是F中的那些规则）是否依然成立？如果成立，说明分解保持了原来的依赖关系；如果不成立，则说明分解改变了原有的依赖。

3.如何判断ρ是否保持F：

我们需要检查在分解后的每个小表中，原始的函数依赖集F是否能够得到保持。具体步骤是：

        1.检查每个小表：

        看原始的函数依赖集F中的每个依赖，是否能在分解后的每个小表中保持成立。

• 如果在某个小表中，原来的函数依赖仍然成立，那么这个小表“保持”了该函数依赖。
• 如果有任何一个小表无法保持某个依赖，那么这个分解就不保持原始的函数依赖集。

        2.合并的关系是否依然符合原始的依赖：

• 如果每个小表保持了原来的函数依赖，合并这些小表后（通过自然连接等方法），原始的依赖关系是否依然成立。

4.对这个问题的分析：

假设我们已经知道了原始的函数依赖集 F={A→B,B→C,A→D,D→C}，并且将关系模式 R(ABCD)分解为 ρ={AB,AC,BD}，我们需要检查：

1. 每个小表上是否保持函数依赖：

   • AB小表：函数依赖 A→B在AB上成立，但其他依赖（例如 B→C，A→D 等）并不成立，因为它们不涉及AB中的列。
   • AC小表：函数依赖 A→B在AC上不成立，因为没有列B；B→C也不成立；而 A→D也没有列D。
   • BD小表：函数依赖 A→D在BD上不成立，因为没有列A；D→C可以成立，因为 DDD 和C在小表中都有列。

2. 合并后的结果是否保持原始依赖：

• 我们还需要考虑当我们将这些小表重新合并时，原始的函数依赖是否依然成立。

5.结论：

• 根据投影的结果，我们可以看到，并不是每个小表都保持了原始函数依赖集 FFF 中的所有依赖。某些依赖在某些小表中无法保持，甚至在合并这些小表时也无法完全恢复原始的依赖关系。
• 因此，ρ不保持F，因为分解后的某些小表没有保持原始的函数依赖。