人工智能-实验3

计科210x 甘晴void

【感悟】本实验值得自己完成一遍

在这里插入图片描述

文章目录

一、实验目的

  • 掌握分类算法的算法思想：朴素贝叶斯算法

  • 编写朴素贝叶斯算法进行分类操作

二、实验平台

  • 课程实训平台https://www.educoder.net/paths/369

三、实验内容

3.0 基础知识

主要是一些概率论基础，如

  • 独立性原理

  • 贝叶斯公式

    • P(b|a) = P(a|b) * P(b) / P(a)

  • 朴素贝叶斯公式

    • 假设所有Effecti各自独立
    • P(Cause,Effect1,……,Effectn) = P(Cause) * Π P(Effecti | Cause)

  • 贝叶斯网络

  • 等

还有python基础，尤其是numpy与对数组的操作。（这个有点折磨，c++到python，还是习惯很笨拙地去遍历数组的每个位置）

3.1 条件概率（选择题）

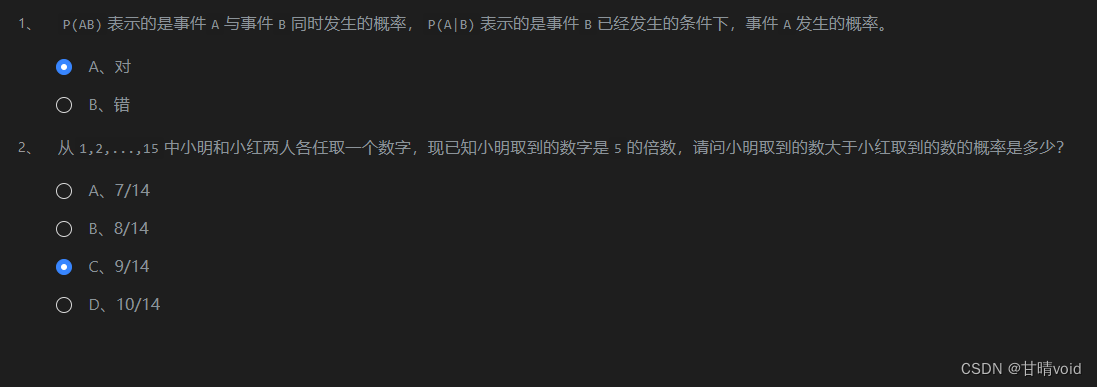
在这里插入图片描述

解析：

（1）为条件概率公式，较为基础

（2）条件概率，求P(小明取到的数>小红取到的数 | 小明取到的数字是5的倍数)。

P(小明取到的数>小红取到的数 | 小明取到的数字是5的倍数) = P(小明取到的数>小红取到的数 && 小明取到的数字是5的倍数) / P( 小明取到的数字是5的倍数)

  • 已知：P( 小明取到的数字是5的倍数) = 1/5
  • 下面计算P(小明取到的数>小红取到的数 && 小明取到的数字是5的倍数)，这是一个古典概型。
  • 总共事件C(2,1)*C(15,2)=210，注意要考虑顺序。
  • 小明取到的数字是5的倍数，只可能是5，10，15。要让小明取到的数大于小红取到的数，这样的事件如下：小明5，小红1,2,3,4；小明10，小红1,2,3,4,5,6,7,8,9；小明15，小红1,2,3,4,5,6,7,8,9,10,11,12,13,14；
  • 这样的情况总数4+9+14=27
  • 故 (27 / 210) / (1 / 5) = 9 / 14

3.2 贝叶斯公式（选择题）

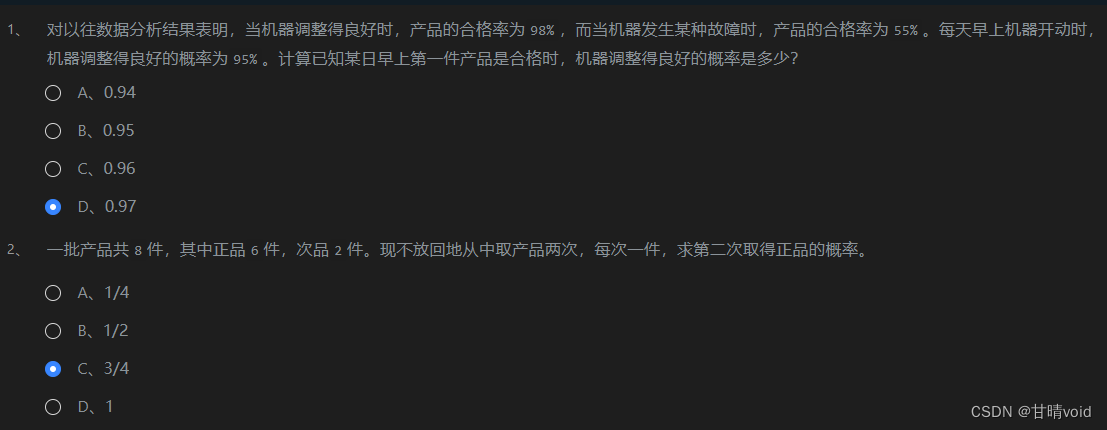
在这里插入图片描述

（1）

P(产品合格 | 机器良好) = 98%

P(产品合格 | 机器故障) = 55%

P(机器良好) = 95%

P(机器良好 | 产品合格)

解：

由贝叶斯公式，P(机器良好 | 产品合格) = [P(产品合格 | 机器良好) * P(机器良好)] / P(产品合格)

由全概率公式，P(产品合格)=P(产品合格 | 机器良好) * P(机器良好) +

P(产品合格 | 机器故障) * P(机器故障) = 98% * 95% + 55% * 5%

综上可得答案约为0.97

（2）分情况讨论

[ C(2,1) * C(6,1) + C(6,1) * C(5,1) / C(8,1) * C(7,1)

答案为3/4

3.3 朴素贝叶斯分类算法流程

3.3.1 算法原理

朴素贝叶斯分类算法是基于贝叶斯定理和特征条件独立性假设的分类方法。对于给定的训练集，基于特征条件独立性假设学习输入输出的联合概率分布(先验概率和条件概率分布)，学习概率分布后，利用贝叶斯定理求出后验概率最大的输出作为预测结果。

形式化抽象如下：

  • 假设类标签（label）为Y={y1,y2,……,yk}，本题中Y={0,1}
  • 假设特征（feature）为A={A1,A2,……,An}，本题中A={颜色，声音，纹理}
  • 假设特征的取值为aij，本题中颜色：用1表示绿色，2表示黄色；声音：用1表示清脆，2表示浑厚。纹理：用1表示清晰，2表示模糊，3表示一般

简单来看，特征只有一个Ai的情况下，问题如下：

  • 模型训练的过程相当于学习P(Ai | Y)，其中B是特定的类别，Ai是特征。
  • 模型预测的过程就是根据贝叶斯公式求P(Y | Ai)的概率。

一般来看，特征为多个A1,A2,……,An。此时根据条件独立性假设，假设这些特征之间相互独立。

本题中，有A1A2A3，原问题被转化为求P(Y | A1A2A3)

注：计算该概率时，假设各个特征之间互不影响，每个特征都是条件独立的。这个假设就是条件独立性假设，可以简化朴素贝叶斯方法，但可能牺牲一定的分类准确性。

即在有各个特征的条件下，预测输入属于哪一个分类的概率，属于哪一个分类的概率最大，就预测输入样本的类别是哪一类。

  • 根据贝叶斯公式，P(Y | A1A2A3)被转换为：
  • P(Y | A1A2A3) = P(YA1A2A3) / P(A1A2A3)
  • = P(Y) * P(A1 | Y) * P(A2 | Y) * P(A3 | Y) / P(A1A2A3)
  • 那么我们想比较P(Y=0 | A1A2A3)和P(Y=1 | A1A2A3)
  • 实际上只要比较P(Y=0) * P(A1 | Y=0) * P(A2 | Y=0) * P(A3 | Y=0)和P(Y=1) * P(A1 | Y=1) * P(A2 | Y=1) * P(A3 | Y=1)的大小关系即可。

下面是整体脉络

  • 训练部分，即根据样本，学习P(Y) 、 P(A1 | Y) 、 P(A2 | Y) 、 P(A3 | Y)这些值。
  • 预测部分，即根据需要预测的特征，以及之前学习的P(Y) 、 P(A1 | Y) 、 P(A2 | Y) 、 P(A3 | Y)这些值，直接计算出P(Y | A1A2A3)。

大致示意图如下

在这里插入图片描述

3.3.2 编程细节

对于训练部分，我们要得到self.label_prob和self.condition_prob即可，前者是一个一维列表/字典，后者是一个三维列表/字典。

self.label_prob较为简单，直接对label分别计数即可得到。

label_0 = np.count_nonzero(label == 0)
        label_1 = np.count_nonzero(label == 1)
        self.label_prob = {0: label_0/label.size, 1: label_1/label.size}

self.condition_prob需要填表，注意到给的训练数据，实际上feature矩阵的每个点有3个特征，feature维度，label，然后是不同样本（不同行），最后才是它自己的值。

我的想法是对于每个样本（每行），确定label和feature维度。此时从3个特征确定了这个值的意义。把它累加到self.condition_prob的对应位置中。

这样遍历完所有样本之后，self.condition_prob的前两维度（label和feature）确定后，得到的是一个关于该feature取值的字典，每个key是该feature的可能取值，value是样本取这个值的个数。这称为一个单位。

之后再对每个这样的单位求概率，得到P(Ai | Y=0/1)，即该瓜是好/坏时，feature取哪个值（例如颜色取黄或绿）的概率。求概率的方法就是将确定该瓜好/坏时，feature取某值的频数除以该feature所有可取值的总频数。

for i in range(2):
	for j in range(feature.shape[1]):
		total_sum = 0
		for key,value in self.condition_prob[i][j].items():
			total_sum += value
		for key,value in self.condition_prob[i][j].items():
			self.condition_prob[i][j][key] /= total_sum

预测时，只要查我们之前算好的表，如P(Y=0 |A1=a A2=b A3=c) = P(Y=0) * P(A1=a | Y=0) * P(A2=b | Y=0) * P(A3=c | Y=0)

这几个值都是已知的。就可以得到答案。

for label_index in range(2):
	j = 0 # 处理的特征序号，即feat的index
	for feat in group:
		pa = self.condition_prob[label_index][j].get(feat)
		if (pa == None):
			prob_list[label_index] *= 0
		else:
			prob_list[label_index] *= pa
		j += 1
3.3.3 代码
import numpy as np
DEBUG = 0

class NaiveBayesClassifier(object):
    def __init__(self):
        self.label_prob = {}
        self.condition_prob = {}

    def fit(self, feature, label):
        '''
        对模型进行训练，需要将各种概率分别保存在self.label_prob和self.condition_prob中
        :param feature: 训练数据集所有特征组成的ndarray
        :param label:训练数据集中所有标签组成的ndarray
        :return: 无返回
        '''
        # ********* Begin *********#
        # label_prob
        label_0 = np.count_nonzero(label == 0)
        label_1 = np.count_nonzero(label == 1)
        self.label_prob = {0: label_0/label.size, 1: label_1/label.size}

        # condition_prob
        self.condition_prob[0] = {}
        self.condition_prob[1] = {}
        # 初始化每个特征取值的字典
        for item in self.condition_prob:
            for feature_index in range(len(feature[0])):  # len(feature[0])为特征数量
                self.condition_prob[item][feature_index] = {}
        # 读取数据
        i = 0  # 样本编号
        for data in feature:
            j = 0  # 特征序号
            for feat in data:
                if (self.condition_prob[label[i]][j].get(feat) == None):
                    self.condition_prob[label[i]][j][feat] = 0
                self.condition_prob[label[i]][j][feat] += 1
                j += 1
            i += 1

        # 归一化得到概率
        for i in range(2):
            for j in range(feature.shape[1]):
                total_sum = 0
                for key,value in self.condition_prob[i][j].items():
                    total_sum += value
                for key,value in self.condition_prob[i][j].items():
                    self.condition_prob[i][j][key] /= total_sum

        if (DEBUG):
            print("label_prob:\n{}".format(self.label_prob))
            print("condition_prob:\n{}".format(self.condition_prob))

# ********* End *********#

    def predict(self, feature):
        '''
        对数据进行预测，返回预测结果
        :param feature:测试数据集所有特征组成的ndarray
        :return:
        '''
        # ********* Begin *********#

        # P(A1) P(B|A1)  P(C|A1)  P(D|A1)
        ans = []
        i = 0 # 处理的组号
        for group in feature:
            if (DEBUG):
                print("now process {}".format(i))
            # 处理多组数据
            prob_list = {}
            prob_list[0] = self.label_prob[0]
            prob_list[1] = self.label_prob[1]
            for label_index in range(2):
                j = 0 # 处理的特征序号，即feat的index
                for feat in group:
                    pa = self.condition_prob[label_index][j].get(feat)
                    if (pa == None):
                        prob_list[label_index] *= 0
                    else:
                        prob_list[label_index] *= pa
                    j += 1
            if (DEBUG):
                print(prob_list[0])
                print(prob_list[1])
            if (prob_list[0]>prob_list[1]):
                ans.append(0)
            else:
                ans.append(1)
            i += 1
        return ans
        # ********* End *********#
        
if __name__ == "__main__":
    nb_classifier = NaiveBayesClassifier()
    feature = np.array([[2, 1, 1],[1, 2, 2],[2, 2, 2],[2, 1, 2],[1, 2, 3]])
    label = np.array([1, 0, 1, 0, 1])
    nb_classifier.fit(feature,label)
    print(nb_classifier.predict(feature))

其中，if __name__ == "__main__"用于本地调试使用，提交的时候将该函数删去。

3.4 拉普拉斯平滑

3.4.1 问题提出

在计算上一题的时候，我们遇到了许多奇怪的地方。

如self.label_prob，即先验概率，如果某个标签根本没有出现，那么它的先验概率就会是0，

如self.condition_prob，这个三维表格中，也有项出现了0，

而上面这两个都是我们最终概率计算式中的乘项。导致了上面我们计算出的概率可能出现0。

这显然是不合理的，所以我们要进行平滑处理，而最常用的方法就是拉普拉斯平滑。

3.4.2 算法原理

拉普拉斯平滑指的是，假设N表示训练数据集总共有多少种类别，Ni表示训练数据集中第i列总共有多少种取值。则训练过程中在算类别的概率时分子加1，分母加N，算条件概率时分子加1，分母加Ni。

就是让0项不出现，用一个很小很小的数来代替。实际上我们这里的拉普拉斯平滑是直接加了1，也有别的处理方法。

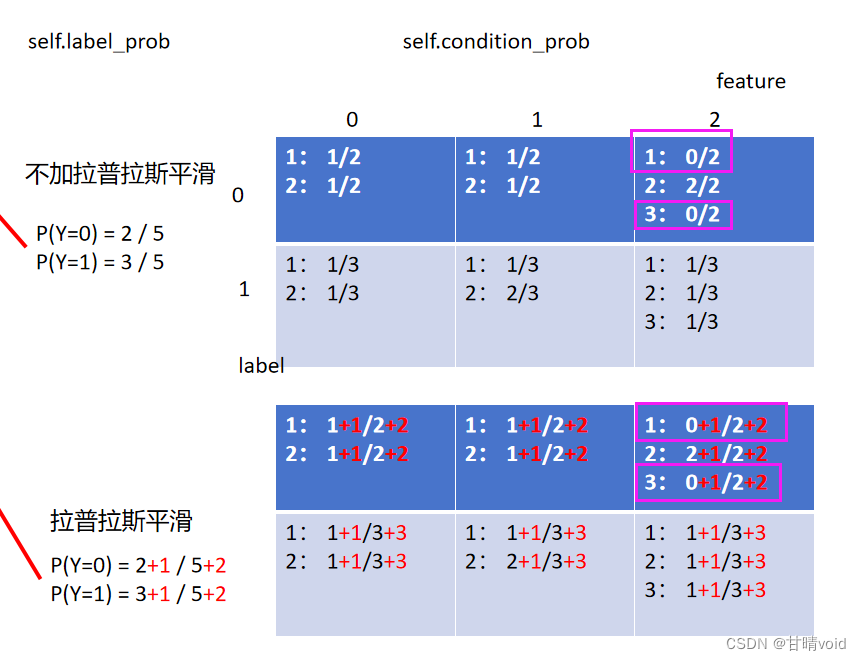
下表标红部分显示了与不加拉普拉斯平滑的区别

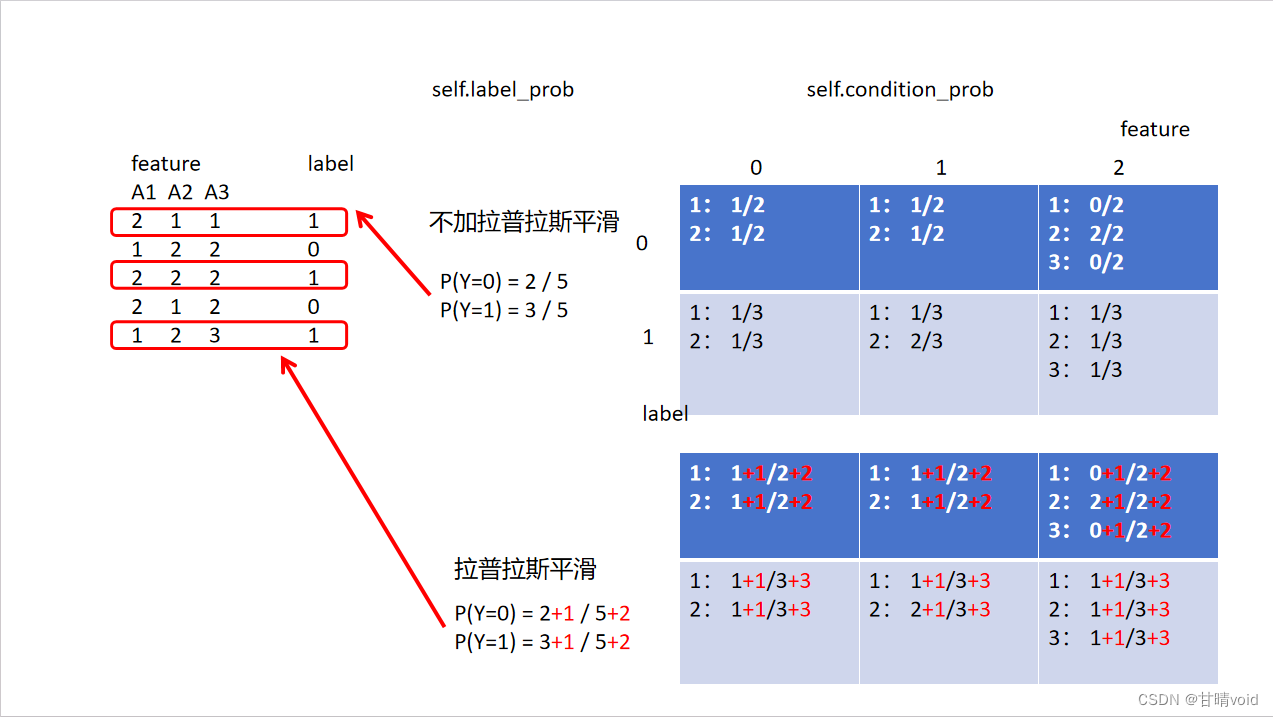
在这里插入图片描述

3.4.3 编程细节

计算self.label_prob时要注意平滑

label_0 = np.count_nonzero(label == 0)
        label_1 = np.count_nonzero(label == 1)
        self.label_prob = {0: (label_0+1)/(label.size+2), 1: (label_1+1)/(label.size+2)}

同样，计算self.condition_prob时也要平滑

for j in range(feature.shape[1]):
            for i in range(2):
                for key,value in self.condition_prob[i][j].items():
                    if (self.condition_prob[(i+1)%2][j].get(key) == None):
                        self.condition_prob[(i+1)%2][j][key] = 0
            Ni = 0
            for key, value in self.condition_prob[i][j].items():
                Ni += 1
            for i in range(2):
                total_sum = Ni
                for key, value in self.condition_prob[i][j].items():
                    total_sum += value
                for key,value in self.condition_prob[i][j].items():
                    self.condition_prob[i][j][key] = (self.condition_prob[i][j][key] + 1) / total_sum

这里因为我是用字典来存的，所以若该项本来为0，我是没有存进字典去的。故这里需要判一下，并对原来没有存入的情况补充存入0，保证每项都有，即下图标粉色的部分。（或许不用字典是更好的方法）

在这里插入图片描述

3.4.4 源码
import numpy as np
DEBUG = 1

class NaiveBayesClassifier(object):
    def __init__(self):
        self.label_prob = {}
        self.condition_prob = {}

    def fit(self, feature, label):
        '''
        对模型进行训练，需要将各种概率分别保存在self.label_prob和self.condition_prob中
        :param feature: 训练数据集所有特征组成的ndarray
        :param label:训练数据集中所有标签组成的ndarray
        :return: 无返回
        '''
        # ********* Begin *********#
        # label_prob
        label_0 = np.count_nonzero(label == 0)
        label_1 = np.count_nonzero(label == 1)
        self.label_prob = {0: (label_0+1)/(label.size+2), 1: (label_1+1)/(label.size+2)}

        # condition_prob
        self.condition_prob[0] = {}
        self.condition_prob[1] = {}
        # 初始化每个特征取值的字典
        for item in self.condition_prob:
            for feature_index in range(len(feature[0])):  # len(feature[0])为特征数量
                self.condition_prob[item][feature_index] = {}
        # 读取数据
        i = 0  # 样本编号
        for data in feature:
            j = 0  # 特征序号
            for feat in data:
                if (self.condition_prob[label[i]][j].get(feat) == None):
                    self.condition_prob[label[i]][j][feat] = 0
                self.condition_prob[label[i]][j][feat] += 1
                j += 1
            i += 1

        # 归一化得到概率(加入拉普拉斯平滑)
        for j in range(feature.shape[1]):
            for i in range(2):
                for key,value in self.condition_prob[i][j].items():
                    if (self.condition_prob[(i+1)%2][j].get(key) == None):
                        self.condition_prob[(i+1)%2][j][key] = 0
            Ni = 0
            for key, value in self.condition_prob[i][j].items():
                Ni += 1
            for i in range(2):
                total_sum = Ni
                for key, value in self.condition_prob[i][j].items():
                    total_sum += value
                for key,value in self.condition_prob[i][j].items():
                    self.condition_prob[i][j][key] = (self.condition_prob[i][j][key] + 1) / total_sum

        if (DEBUG):
            print("label_prob:\n{}".format(self.label_prob))
            print("condition_prob:\n{}".format(self.condition_prob))

# ********* End *********#
    def predict(self, feature):
        '''
        对数据进行预测，返回预测结果
        :param feature:测试数据集所有特征组成的ndarray
        :return:
        '''
        # ********* Begin *********#
        # P(A1) P(B|A1)  P(C|A1)  P(D|A1)
        ans = []
        i = 0 # 处理的组号
        for group in feature:
            if (DEBUG):
                print("now process {}".format(i))
            # 处理多组数据
            prob_list = {}
            prob_list[0] = self.label_prob[0]
            prob_list[1] = self.label_prob[1]
            for label_index in range(2):
                j = 0 # 处理的特征序号，即feat的index
                for feat in group:
                    pa = self.condition_prob[label_index][j].get(feat)
                    if (pa == None):
                        prob_list[label_index] *= 0
                    else:
                        prob_list[label_index] *= pa
                    j += 1
            if (DEBUG):
                print(prob_list[0])
                print(prob_list[1])
            if (prob_list[0]>prob_list[1]):
                ans.append(0)
            else:
                ans.append(1)
            i += 1
        return ans
        # ********* End *********#

if __name__ == "__main__":
    nb_classifier = NaiveBayesClassifier()
    feature = np.array([[2, 1, 1],[1, 2, 2],[2, 2, 2],[2, 1, 2],[1, 2, 3]])
    label = np.array([1, 0, 1, 0, 1])
    nb_classifier.fit(feature,label)
    print(nb_classifier.predict(feature))

3.5 新闻文本主题分类

3.5.1 问题解析

使用sklearn完成新闻文本主题分类任务。

这个问题基本上就是教我们使用调包。

3.5.2 算法原理

①文本向量化

将文本转为向量，CountVectorizer，有点类似于大模型中的分词器，是自然语言预处理的一部分。

题目提到，仅使用仅仅通过CountVectorizer会出现问题：统计词频的方式来将文本转换成向量，长的文章词语出现的次数会比短的文章要多，而实际上两篇文章可能谈论的都是同一个主题。

为了解决这个问题，我们可以使用tf-idf来构建文本向量，sklearn中已经提供了tf-idf的接口。注意到该种方法是之前方法的改进版，故直接替代了上面的CountVectorizer

②MultinomialNB

MultinomialNB是sklearn中多项分布数据的朴素贝叶斯算法的实现，并且是用于文本分类的经典朴素贝叶斯算法。在本关中建议使用MultinomialNB来实现文本分类功能。

我们将它实例化之后，调用它就可以实现贝叶斯分类。

同样，要考虑拉普拉斯平滑。在MultinomialNB实例化时alpha是一个常用的参数。alpha: 平滑因子。当等于1时，做的是拉普拉斯平滑；当小于1时做的是Lidstone平滑；当等于0时，不做任何平滑处理。

都比较好理解，直接写代码就可以了。

3.5.3 源码

from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB


def news_predict(train_sample, train_label, test_sample):
    '''
    训练模型并进行预测，返回预测结果
    :param train_sample: 原始训练集中的新闻文本，类型为ndarray
    :param train_label: 训练集中新闻文本对应的主题标签，类型为ndarray
    :param test_sample: 原始测试集中的新闻文本，类型为ndarray
    :return: 预测结果，类型为ndarray
    '''

    # 实例化tf-idf对象，同时完成向量化和TF-IDF转换
    tfidf_vectorizer = TfidfVectorizer()

    # 将训练集和测试集的文本进行向量化和TF-IDF转换
    X_train = tfidf_vectorizer.fit_transform(train_sample)
    X_test = tfidf_vectorizer.transform(test_sample)

    # 使用多项式朴素贝叶斯进行训练和预测
    clf = MultinomialNB(alpha=0.001)
    clf.fit(X_train, train_label)
    result = clf.predict(X_test)

    return result

四、思考题

如何在参数学习或者其他方面提高算法的分类性能？

这个问题有点大，应该也是现在学界还在不断努力解决的问题之一（论文嘎嘎发）。依据我目前的眼界与经验，只能总结出一部分回答。

  • 特征工程优化： 精心选择和设计特征可以显著提高分类器的性能。这可能包括特征选择、特征变换、特征组合等方法，以增强模型对数据的表达能力。
  • 模型选择： 根据问题的特点选择合适的分类算法。不同的问题可能需要不同类型的模型，如决策树、支持向量机、神经网络等。
  • 调参优化： 对于参数学习算法，通过调整参数来优化模型性能。这可以通过网格搜索、随机搜索、贝叶斯优化等技术来实现，以找到最佳的参数组合。
  • 交叉验证： 使用交叉验证技术来评估模型的泛化能力，并选择最佳的模型参数。
  • 集成学习： 使用集成学习方法，如随机森林、梯度提升树等，将多个模型的预测结果进行组合，以获得更好的分类性能。
  • 数据增强： 对训练数据进行增强，如旋转、平移、缩放等操作，以扩大训练集的规模和多样性，从而提高模型的泛化能力。
  • 处理不平衡数据： 对于不平衡的数据集，采用采样技术（如过采样、欠采样）或者使用特殊的损失函数来处理样本不均衡问题。
  • 正则化： 使用正则化技术，如L1正则化、L2正则化等，以防止模型过拟合。
  • 特定领域知识应用： 利用领域专业知识对算法进行定制或者调整，以提高模型在特定领域的性能。
  • 持续学习与优化： 不断尝试新的算法、新的技术，并根据实验结果进行调整和优化，以提高分类器的性能。

参考文献

  • A橙：https://blog.csdn.net/Aaron503/article/details/131104758
Logo
EazyDevelop社区

一站式 AI 云服务平台

更多推荐

cover

5分钟搞定！MySQL/PostgreSQL 到 Elasticsearch 的实时同步

avatar EazyDevelop社区
cover

两小时，我搭了一套销售提成计算系统

avatar EazyDevelop社区
cover

零代码时代：如何利用聚合API平台快速构建你的专属AI Agent

avatar EazyDevelop社区