python编程人工智能小例子,python人工智能有趣例子
需要注意的是,根节点没有父节点,故父节点的α和β值分别设置为负无穷和正无穷。叶子节点不需要向下拓展,而是直接进行打分。打分同时作为该叶子节点的 α \alpha α和 β \beta β值即可将叶子节点也视作中间节点,方便统一处理。大家好,小编为大家解答python编程人工智能小例子的问题。很多人还不知道python人工智能有趣例子,现在让我们一起来看看吧!人工智能实验博弈树搜索 1。人工智能实验
·
大家好,小编为大家解答python编程人工智能小例子的问题。很多人还不知道python人工智能有趣例子,现在让我们一起来看看吧!

人工智能实验博弈树搜索
博弈树搜索
目录
人工智能实验博弈树搜索 1
博弈树搜索 1
- 算法原理 1
1.1 博弈树 1
1.2 Alpha-beta剪枝 2
1.2.1 Max节点的剪枝 2
12.2 Min节点的剪枝 2 - 流程图和伪代码 3
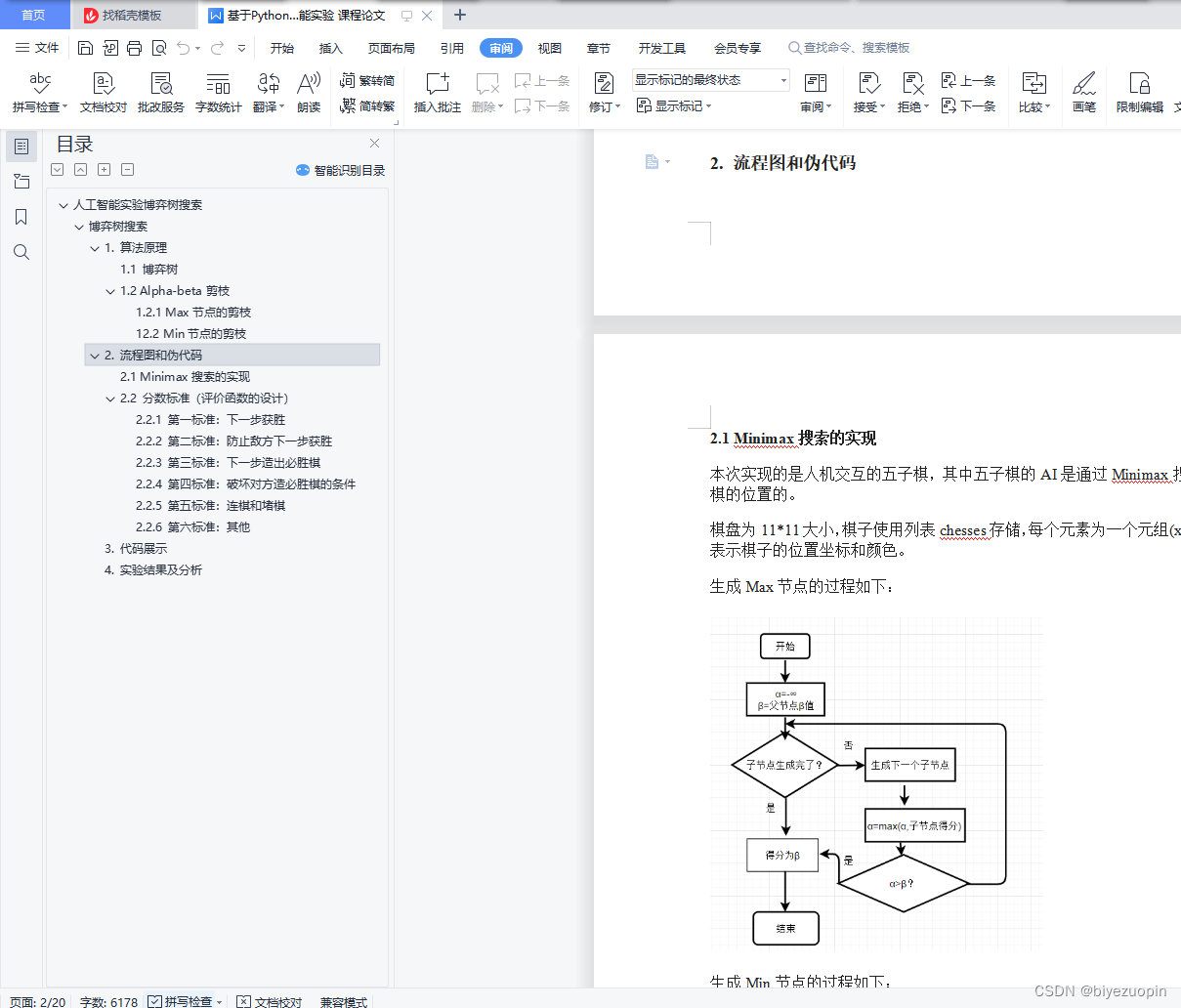
2.1 Minimax搜索的实现 3
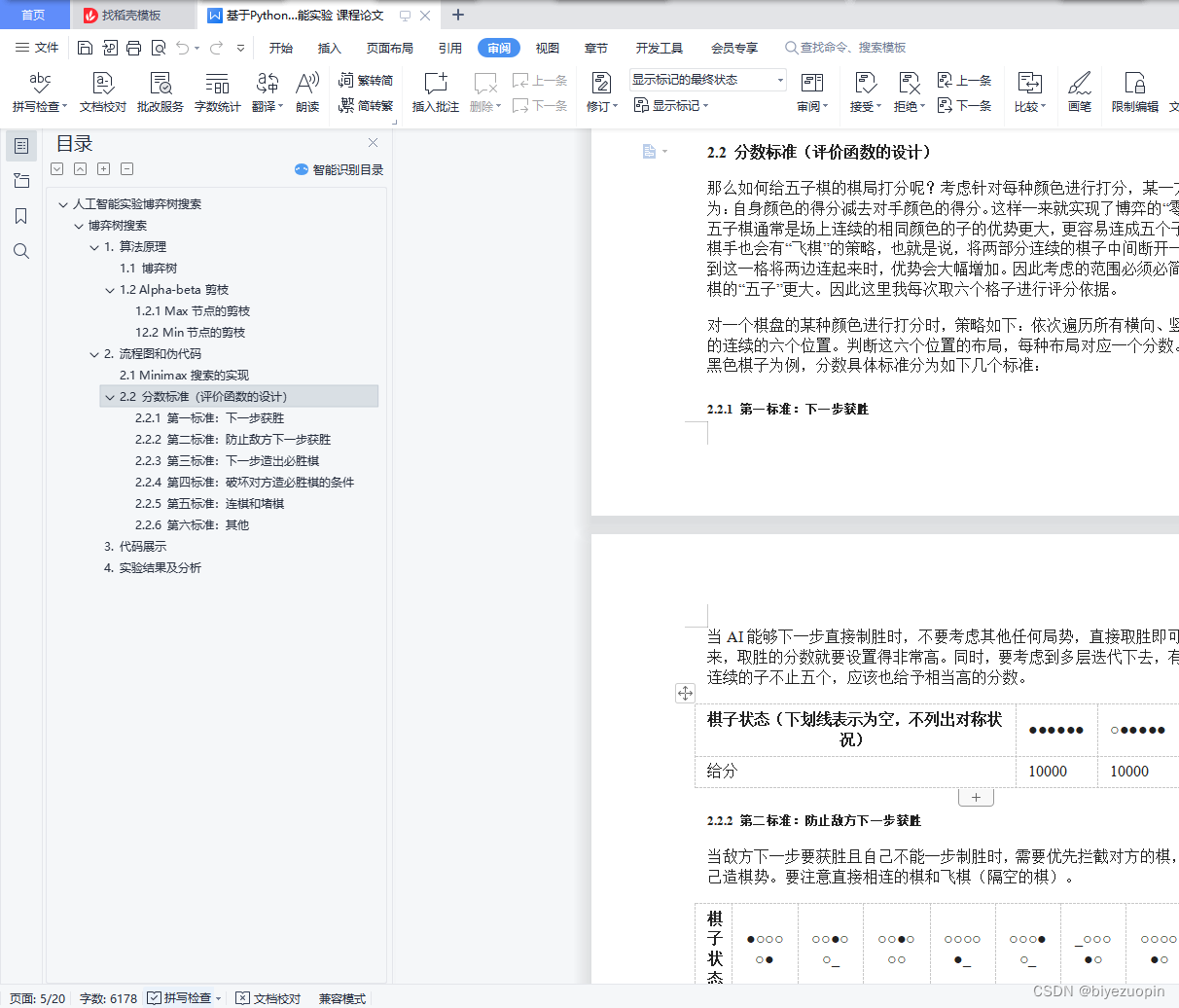
2.2 分数标准(评价函数的设计) 5
2.2.1 第一标准:下一步获胜 5
2.2.2 第二标准:防止敌方下一步获胜 6
2.2.3 第三标准:下一步造出必胜棋 6
2.2.4 第四标准:破坏对方造必胜棋的条件 6
2.2.5 第五标准:连棋和堵棋 6
2.2.6 第六标准:其他 7 - 代码展示 7
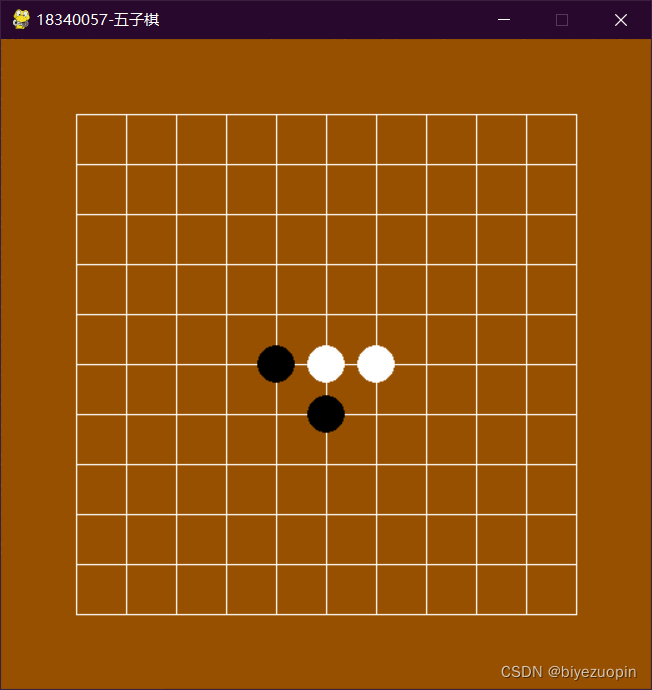
- 实验结果及分析 14
1.1 博弈树
博弈树针对的是二人零和博弈的问题,二人轮流行动,行动时令自己的优势最大。二人零和博弈有如下特点:
确定性:二人的行动有多种选择,但最终的行动是确定的
信息完备性:博弈双方知道当前局势(即空间状态)的全部信息
零和性:一方的损失等于另一方的收益,二者得分相加恒为零
由以上特点,我们可以构造博弈树python自动化运维系统。因为信息完备性和确定性,可以用博弈树的每个节点表示一个确定的状态,在动作后得到的新状态作为子节点。对于每个状态都有同一个评价函数来评估双方的得分。因为零和性,一方通过决策使得自身的评价函数尽可能的大,另一方让队手的评价函数尽可能的小。因为二者是轮流行动的,在树的每一层让一方的评价函数取最大和最小交替进行。
由上述的特性,博弈树的搜索过程又被称为minimax搜索。博弈双方行动逐层交替,将评价函数值看做一方的分数,在那一方行动时要让分数尽可能的大,这样的节点被称为Max节点;在另一方行动时要让分数尽可能的小,这样的节点被称为Min节点。
要让一方的下一步采取最优的策略,需要进行树的搜索。在实际问题中,树往往非常大,因此只考虑一定的深度,而不是整个遍历。进行深入搜索时,轮流考虑Max节点和Min节点,每次都采取最优策略,最终得到本步的最优策略。
1.2 Alpha-beta剪枝
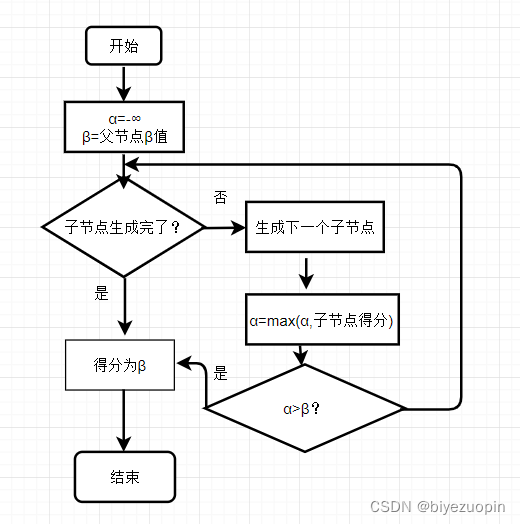
通过Alpha-beta剪枝可以对minimax搜索进行剪枝。在博弈树的每个节点保存两个值: α \alpha α表示在该节点能达到的分数的下界,初始化为 − ∞ -\infin −∞, β \beta β表示该节点能达到的分数的上界,初始化为 ∞ \infin ∞。
Min节点和Max节点的生成和剪枝可以用同一个函数通过递归实现。
input:type, state, depth, last_a, last_b
/* 输入:节点类型、 当前状态、深度(越大则越浅)、父节点的α和β值 */
output: act, a, b
/* 输出:当前节点取到极值的动作、当前节点的α和β值 */
def NodeSummon(type, state, depth, last_a, last_b):
/* 生成叶子节点则直接打分 */
if depth == 0 then return Null, getScore(state),getScore(state)
/* 依据节点类型初始化α和β值 */
a = -infin
b = infin
if type == Max then b = last_b
else a = last_a
/* 遍历每个可行的动作 */
for eachAct that possible
newState = changeState(state, eachAct) /* 依据动作改变当前状态 */
_, next_a, next_b = NodeSummon(type, chesses, depth-1, a, b) /* 递归生成子节点 */
/* 依据节点类型更新α或β值,保存取极值的状态 */
if type == Max && a<next_a then
act = eachAct
a = next_a
if type == Min && b>next_b then
act = eachAct
b = next_b
/* 剪枝判断 */
if a>b then return act, a, b
end
return act, a, b
需要注意的是,根节点没有父节点,故父节点的α和β值分别设置为负无穷和正无穷。叶子节点不需要向下拓展,而是直接进行打分。打分同时作为该叶子节点的 α \alpha α和 β \beta β值即可将叶子节点也视作中间节点,方便统一处理。

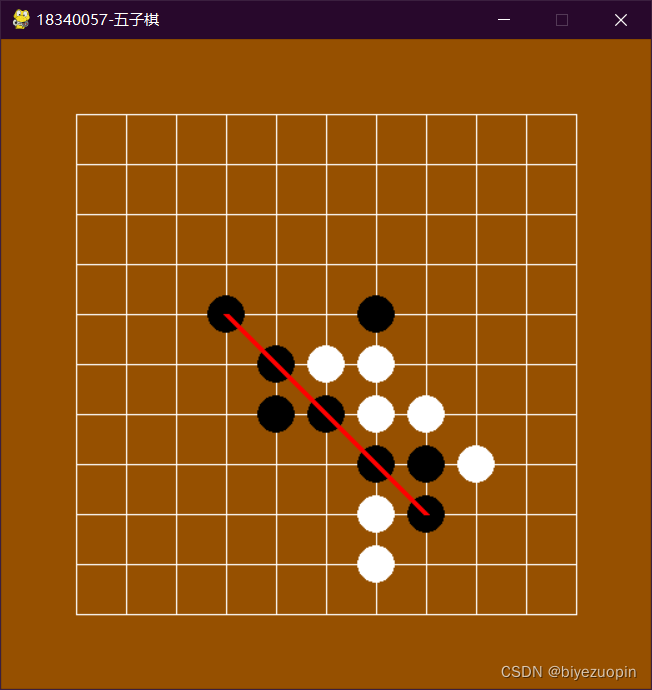
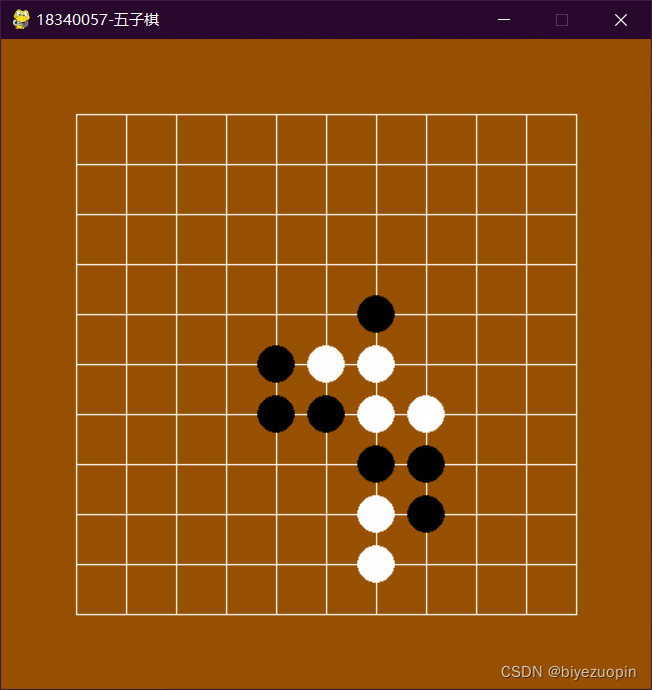
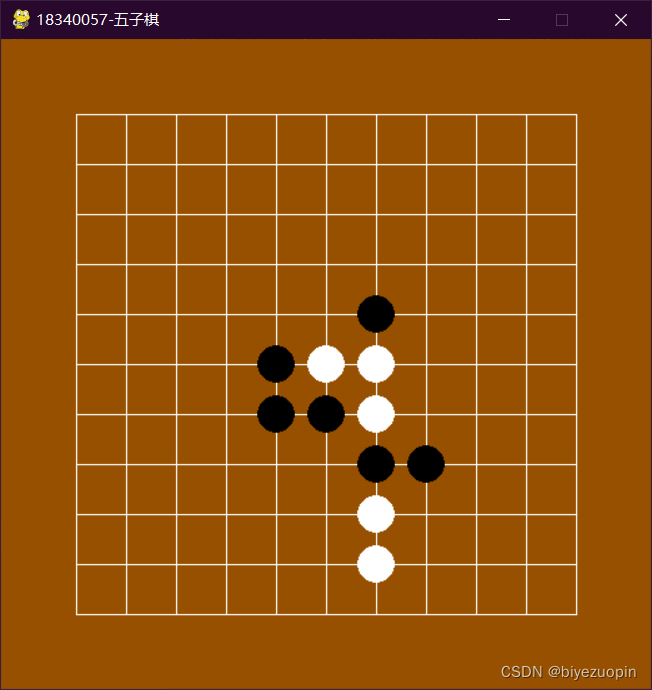
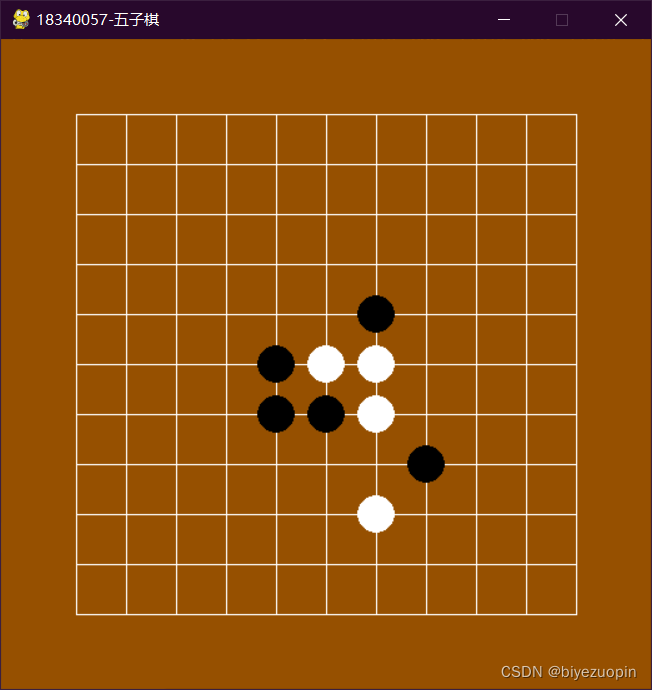







更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容










所有评论(0)