---

一、马尔可夫链的定义与特点

定义

• 马尔可夫链是一个由状态（state）组成的序列，状态之间的转移依赖于当前状态，但不依赖于之前的状态历史。
• 换句话说，当前状态的信息足以决定下一个状态的分布，这就是所谓的马尔可夫性（Markov property）。

数学表达式为：
$$P(q_i|q_{i-1},q_{i-2},\dots ,q_1)=P(q_i|q_{i-1})$$
这种假设称为一阶马尔可夫假设（First-order Markov assumption）。

---

特点

1. 状态集合（States, $N$）：

   • 一组有限的状态，记为 N={q1,q2,…,qn}N = \{q_1, q_2, \dots, q_n\}N={q1​,q2​,…,qn​}。
   • 例如，一个天气系统可能有三种状态：冷（Cold）、热（Hot）、温暖（Warm）。

2. 状态转移概率矩阵（Transition Probability Matrix, $A$）：

   • 表示从一个状态转移到另一个状态的概率，记为 $a_{ij}=P(q_j|q_i)$。
   • 每一行的概率总和为1：
     $$\sum _j{a}_{ij}=1,\forall i$$

3. 初始状态分布（Initial Probability Distribution, $\pi$）：

   • 描述系统开始时每个状态的概率，记为 ${\pi }_i=P(q_i)$。

---

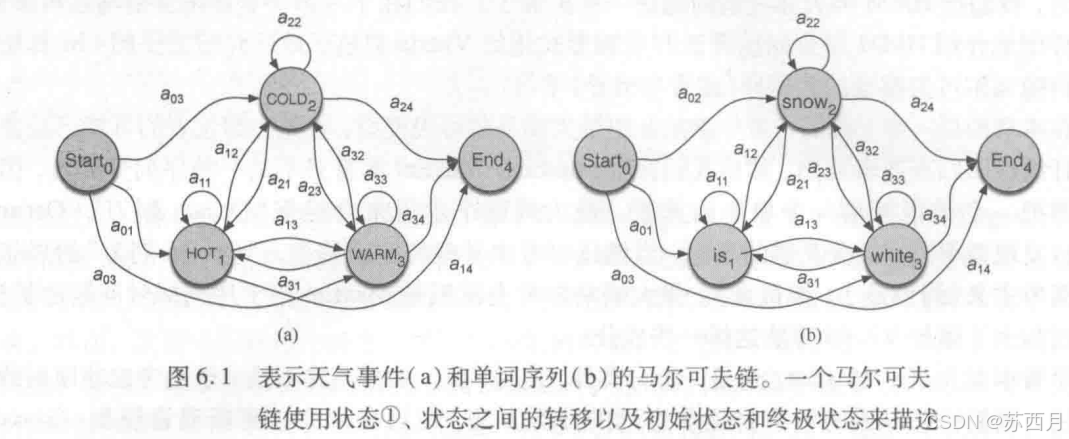
二、马尔可夫链的图模型

• 图表示法：马尔可夫链可以用**有向图（Graph）**表示，节点表示状态，边表示状态转移概率。
• 例如，天气的马尔可夫链：
  • 节点：冷（Cold）、热（Hot）、温暖（Warm）。
  • 边上的数值：对应状态转移概率。

生活例子：
假设你每天的心情有三种可能的状态：开心（Happy）、一般（Neutral）、难过（Sad）。假如：

1. 如果今天开心，那么明天继续开心的概率是 0.6，变成一般的概率是 0.3，变成难过的概率是 0.1。
2. 如果今天一般，明天变开心、一般和难过的概率分别是 0.4、0.4 和 0.2。
3. 如果今天难过，明天变开心、一般和难过的概率分别是 0.3、0.3 和 0.4。

这就可以用一个图表示出来，每种心情是一个节点，边上的概率表示从一种心情转变到另一种心情的可能性。

---

三、关键公式及其理解

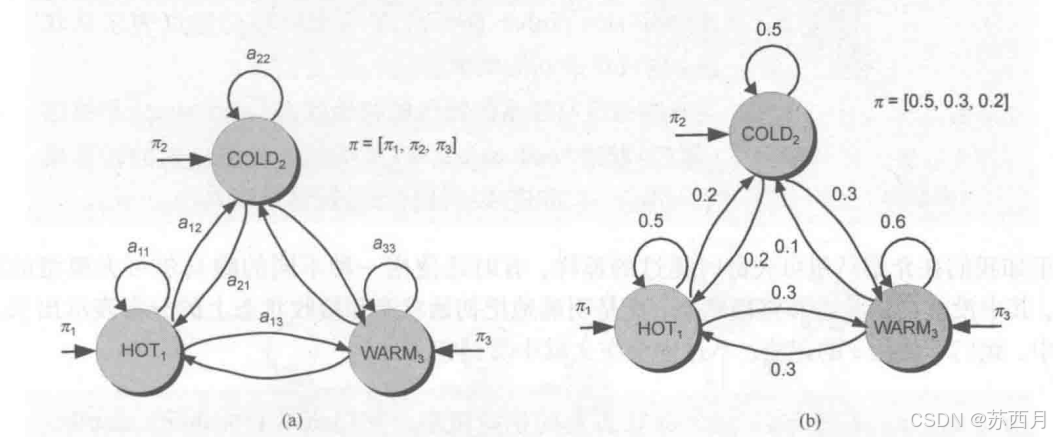
1. 状态转移概率矩阵的性质

$$\sum _j{a}_{ij}=1$$
解释：从某个状态出发（例如“冷”），转移到所有可能状态（冷、热、温暖）的概率总和为1。

生活例子：假设你在某个十字路口有三条路可以走，选择每条路的概率是 0.5、0.3 和 0.2，总和必须是 1。

---

2. 初始状态分布

$$\sum _i{\pi }_i=1$$
解释：系统的初始状态总有一个分布，例如刚开始时“冷”、“热”、“温暖”的概率分别是 0.3、0.5 和 0.2，总和也必须为 1。

---

3. 马尔可夫性质

$$P(q_i|q_{i-1},q_{i-2},\dots )=P(q_i|q_{i-1})$$
解释：当前状态 $q_i$ 只依赖于前一个状态 $q_{i-1}$，不需要关注更早的状态。

生活例子：假设你每天的穿衣选择（外套或短袖）只依赖于当天的天气，而与之前几天的天气无关。

---

四、结合例题理解

例题中给出了两组序列：

1. $\text{hot, hot, hot}$
2. $\text{cold, hot, cold, hot}$

通过状态转移矩阵 $A$，你可以计算出每种序列的概率。计算步骤如下：

1. 根据初始状态概率 $\pi$，确定第一个状态的概率。
2. 根据状态转移概率矩阵 $A$，依次计算后续状态的转移概率。
3. 将所有状态转移概率相乘，得到整个序列的概率。

---