深度学习 神经网络(3)反向传播与计算图
前面我们实现了前馈神经网络的前向传播,即输入层开始,通过逐层传播计算,最终计算出输出层结果。这篇文章介绍的是怎么通过链式求导法则来进行反向传播更新权重参数,以及通过计算图来更加直观地求偏导
一、前言
前面我们实现了前馈神经网络的前向传播,即输入层开始,通过逐层传播计算,最终计算出输出层结果。
这篇文章介绍的是怎么通过链式求导法则来进行反向传播更新权重参数,以及通过计算图来更加直观地求偏导。
二、损失函数
激活函数不一样,损失函数也可能有所不同。比如:
2.1 线性回归问题
如房价预测,输出是一个连续值,使用均方误差损失函数:
L ( y ^ ( i ) , y ( i ) ) = ∑ i = 1 m [ y ^ ( i ) − y ( i ) ] 2 L(\hat y^{(i)},y^{(i)})=\sum_{i=1}^m[\hat y^{(i)}-y^{(i)}]^2 L(y^(i),y(i))=i=1∑m[y^(i)−y(i)]2
其中 y ^ ( i ) \hat y^{(i)} y^(i)为第 i i i 个实例的预测值, y ( i ) y^{(i)} y(i)为真实值。
2.2 二分类问题
如垃圾邮件判断,最后一层的激活函数是sigmoid,输出0~1的值,使用二分类交叉熵损失函数:
L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) ln y ^ ( i ) + ( 1 − y ( i ) ) × ln ( 1 − y ^ ( i ) ) ] L(\hat y^{(i)},y^{(i)})=-\frac1{m}\sum_{i=1}^m[y^{(i)}\ln \hat y^{(i)}+(1-y^{(i)})×\ln(1-\hat y^{(i)})] L(y^(i),y(i))=−m1i=1∑m[y(i)lny^(i)+(1−y(i))×ln(1−y^(i))]
2.2 多分类问题
如商品分类,最后一层的激活函数是softmax,输出0~1的值,使用多分类交叉熵损失函数:
L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m ∑ j = 1 k Y j ( i ) ln ( y ^ j ( i ) ) L(\hat y^{(i)},y^{(i)})=-\frac1m\sum_{i=1}^m\sum_{j=1}^kY^{(i)}_j\ln(\hat y^{(i)}_j) L(y^(i),y(i))=−m1i=1∑mj=1∑kYj(i)ln(y^j(i))
其中 Y Y Y是 y y y的独热编码矩阵, k k k是输出结果个数, y ^ j ( i ) \hat y^{(i)}_j y^j(i)第 j j j 个预测输出。
三、反向传播
反向传播即损失函数对各 w w w 参数求偏导,反向更新 w w w参数值,进行梯度下降收敛,使得损失函数最小。
前面的系列文章有进行过线性回归问题、二分类问题和多分类问题损失函数求偏导进行梯度下降的公式推导,读者可以参考。
如果按照之前线性和逻辑回归的梯度下降方法,对 w w w参数逐一计算,很耗计算资源、而且人为计算非常容易出错。尤其是在多层神经网络结构中,每层有不同的激活函数,每层的 w w w参数求导公式都不一样,参数求导的复杂度极大提升。
主要还是遵循链式求导法则进行推导,为节约时间和脑力,在此不做推导计算,直接进入计算图方法。
四、计算图
计算图的基本原理是所有的数值计算可以分解为一些基本操作,包含 +, −, ×, / 和一些初等函数 exp, log,sin, cos 等,然后利用链式法则来自动计算一个复合函数的梯度。
我们以下面这个函数为例:
h ( x ) = 1 1 + e − w x h(x)=\frac1{1+e^{-wx}} h(x)=1+e−wx1
将 h ( x ) h(x) h(x)进行拆分成最简单的数学运算,构成计算图: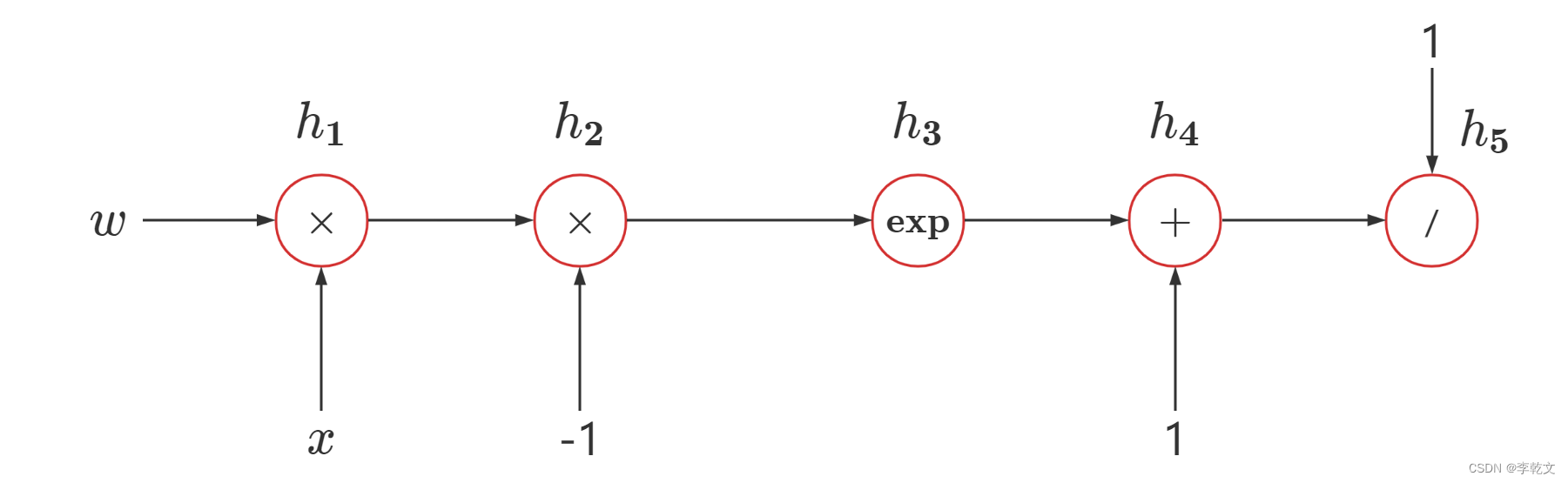
计算图各个节点处的计算都是局部计算,可以让我们集中精力于局部计算。
比如 h 4 = h 3 + 1 h_4=h_3+1 h4=h3+1,那么 ∂ h 4 ∂ h 3 = 1 \frac{∂h_4}{∂h_3}=1 ∂h3∂h4=1。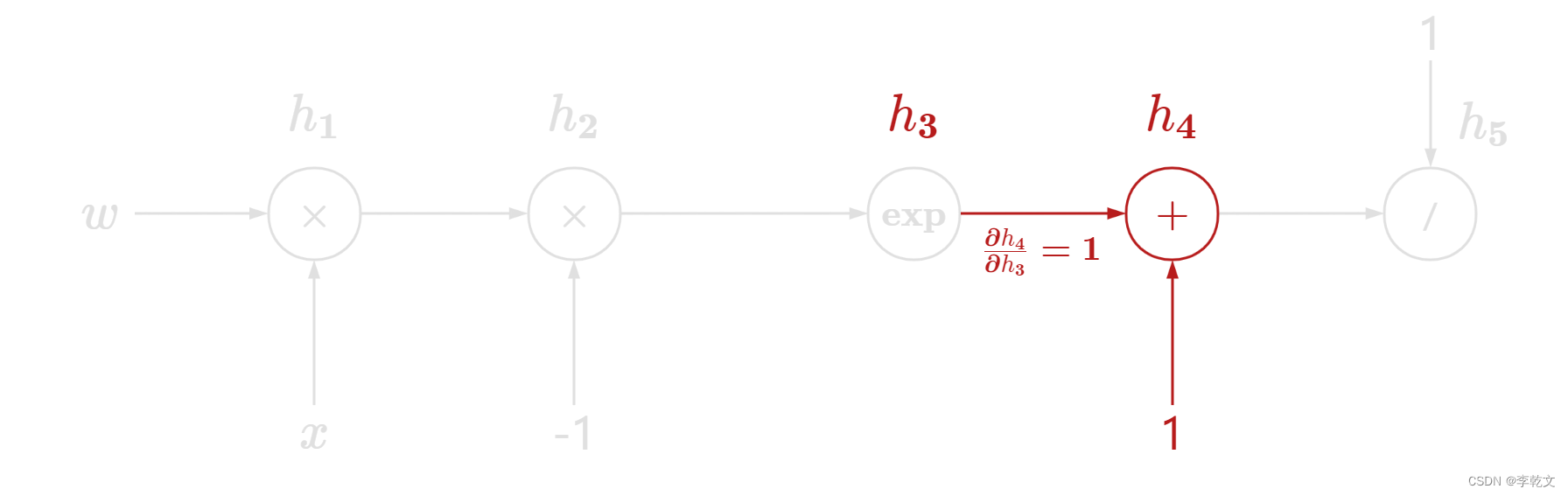
下面可以非常方便地列出计算图各节点的偏导函数: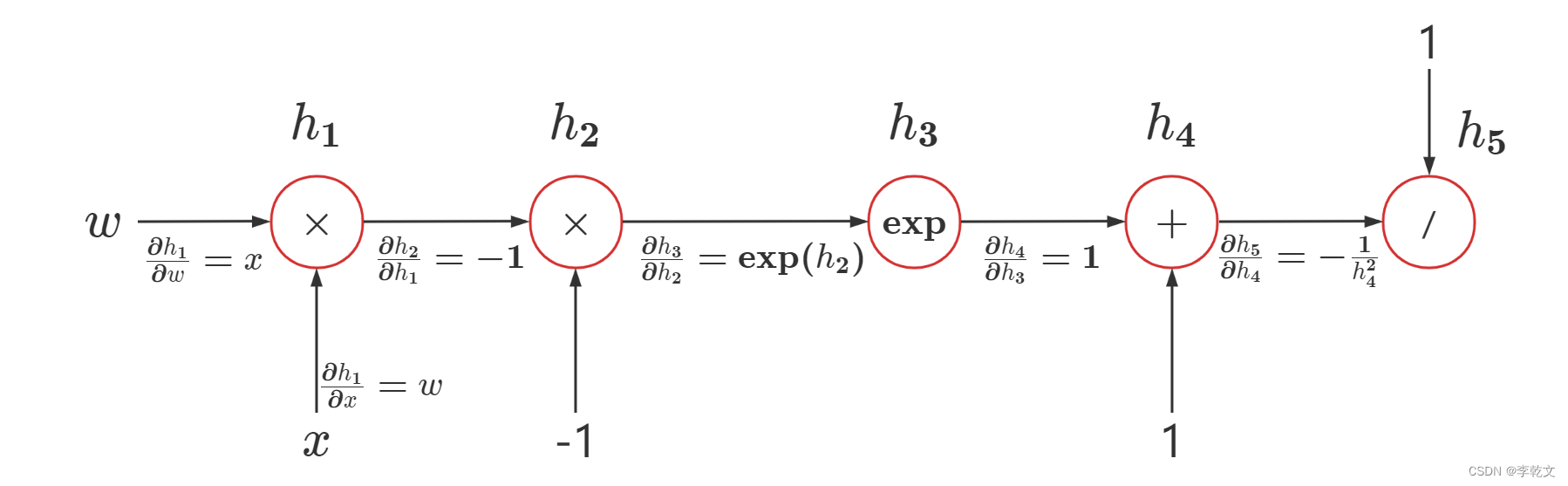
表格形式:
| 函数 | 导数 |
|---|---|
| h 1 = w x h_1=wx h1=wx | ∂ h 1 ∂ w = x 、 ∂ h 1 ∂ x = w \frac{∂h_1}{∂w}=x、\frac{∂h_1}{∂x}=w ∂w∂h1=x、∂x∂h1=w |
| h 2 = h 1 × ( − 1 ) h_2=h_1\times(-1) h2=h1×(−1) | ∂ h 2 ∂ h 1 = − 1 \frac{∂h_2}{∂h_1}=-1 ∂h1∂h2=−1 |
| h 3 = exp ( h 2 ) h_3=\exp(h_2) h3=exp(h2) | ∂ h 3 ∂ h 2 = exp ( h 2 ) \frac{∂h_3}{∂h_2}=\exp(h_2) ∂h2∂h3=exp(h2) |
| h 4 = 1 + h 3 h_4=1+h_3 h4=1+h3 | ∂ h 4 ∂ h 3 = 1 \frac{∂h_4}{∂h_3}=1 ∂h3∂h4=1 |
| h 5 = 1 h 4 h_5=\frac1{h_4} h5=h41 | ∂ h 5 ∂ h 4 = 1 ( h 4 ) 2 \frac{∂h_5}{∂h_4}=\frac1{(h_4)^2} ∂h4∂h5=(h4)21 |
链式求导计算图: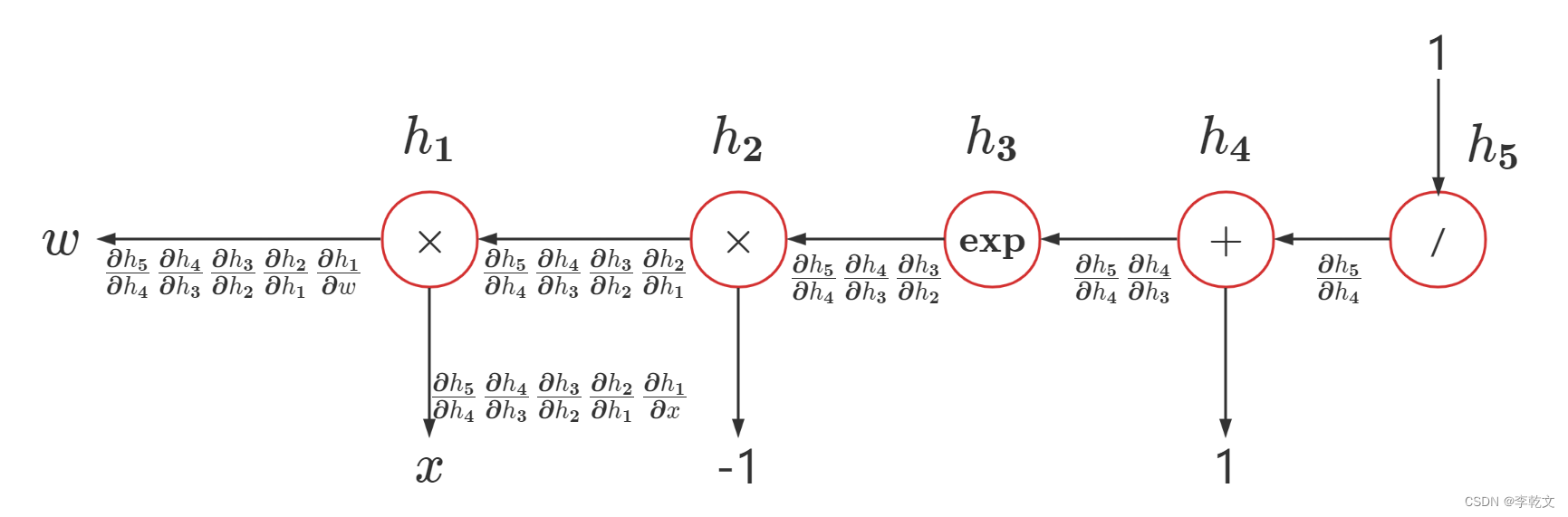
按照链式求导法则,要对 h ( x ) h(x) h(x)对 w w w求偏导,对比上述计算图,有:
∂ h ( x ) ∂ w = ∂ h 5 ∂ h 4 ∂ h 4 ∂ h 3 ∂ h 3 ∂ h 2 ∂ h 2 ∂ h 1 ∂ h 1 ∂ w \begin{aligned} \frac{∂h(x)}{∂w}&=\frac{∂h_5}{∂h_4}\frac{∂h_4}{∂h_3}\frac{∂h_3}{∂h_2}\frac{∂h_2}{∂h_1}\frac{∂h_1}{∂w}\\ \end{aligned} ∂w∂h(x)=∂h4∂h5∂h3∂h4∂h2∂h3∂h1∂h2∂w∂h1
以 ∂ h ( x ) ∂ w \frac{∂h(x)}{∂w} ∂w∂h(x)为例,当 x = 1 , w = 0 x=1,w=0 x=1,w=0 时,代入计算图可得: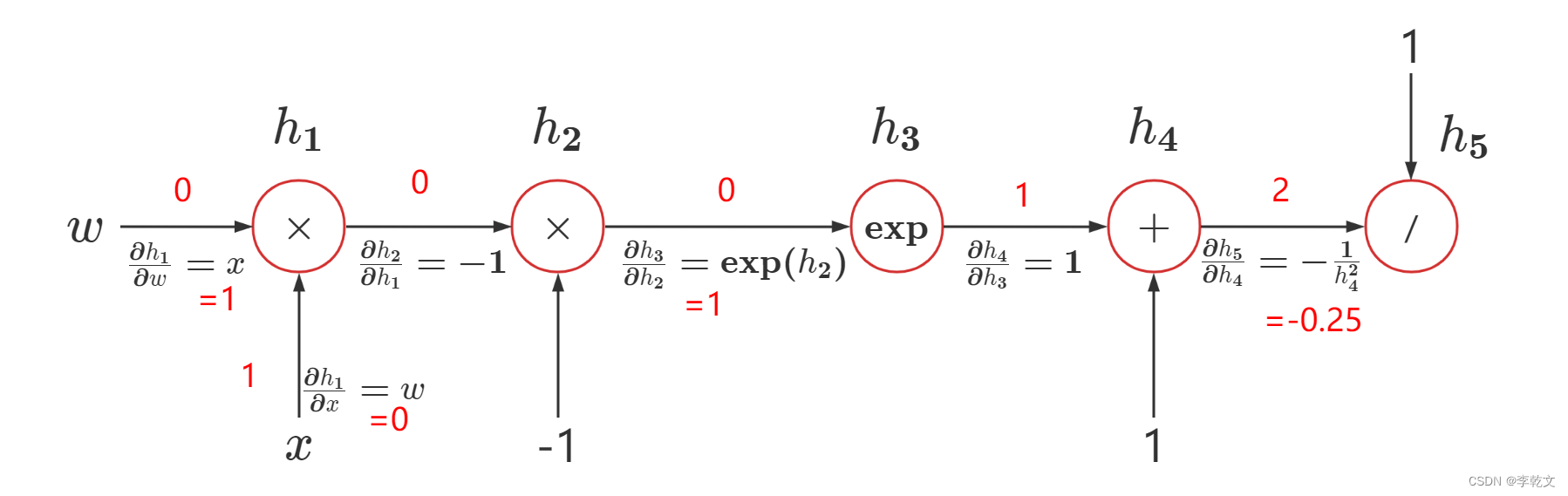
∂ h ( x ) ∂ w ∣ x = 1 , w = 0 = ∂ h 5 ∂ h 4 ∂ h 4 ∂ h 3 ∂ h 3 ∂ h 2 ∂ h 2 ∂ h 1 ∂ h 1 ∂ w = − 0.25 × 1 × 1 × ( − 1 ) × 1 = 0.25 \begin{aligned} \frac{∂h(x)}{∂w}|_{x=1,w=0}&=\frac{∂h_5}{∂h_4}\frac{∂h_4}{∂h_3}\frac{∂h_3}{∂h_2}\frac{∂h_2}{∂h_1}\frac{∂h_1}{∂w}\\ &=-0.25\times1\times 1\times(-1)\times 1\\ &=0.25 \end{aligned} ∂w∂h(x)∣x=1,w=0=∂h4∂h5∂h3∂h4∂h2∂h3∂h1∂h2∂w∂h1=−0.25×1×1×(−1)×1=0.25
使用计算图,只需要关注局部节点的输入输出,整个流程不需要复杂的计算。
那么如何用代码来实现计算图的自动求导呢?
到这一步,我们了解其原理思想就行了。
在目前大部分深度学习框架都支持自动求导,Theano 和 Tensorflow 采用的是静态计算图,而DyNet、Chainer 和 PyTorch 采用的是动态计算图.Tensorflow 2.0 也支持了动态计算图。
五、参考资料
《神经网络与深度学习-邱锡鹏》
《深度学习入门:基于Python的理论与实现》
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容










所有评论(0)