1、机器学习算法(ML)

1.1分类

根据训练方法分为三类：监督学习、非监督学习、强化学习

通过训练集，不断识别特征，不断建模，最后形成有效的模型，这个过程就叫“机器学习”！

1.2监督学习类

监督学习是指我们给算法一个数据集，并且给定正确答案。机器通过数据来学习正确答案的计算方法。例子：我们准备了一大堆猫和狗的照片，我们想让机器学会如何识别猫和狗。当我们使用监督学习的时候，我们需要给这些照片打上标签。

1.2.1线性回归

线性回归

①回归和分类（有的分类也可以转化为回归）

回归算法是相对分类算法而言的，与我们想要预测的目标变量y的值类型有关。

如果目标变量y是分类型变量，如预测用户的性别（男、女），预测月季花的颜色（红、白、黄……），预测是否患有肺癌（是、否），那我们就需要用分类算法去拟合训练数据并做出预测；

如果y是连续型变量，如预测用户的收入（4千，2万，10万……），预测员工的通勤距离（500m，1km，2万里……），预测患肺癌的概率（1%，50%，99%……），我们则需要用回归模型。

其实有时分类问题也可以转化为回归问题，例如肺癌预测，先用回归算法预测出肺癌的概率，再给定一个阈值，利用阈值划分分类。

②一元线性回归

当我们只用一个x来预测y，就是一元线性回归，线性回归就是要找一条直线，并且让这条直线尽可能地拟合图中的数据点。数学理论的世界是精确的。但现实世界中的数据就像这个散点图，我们只能尽可能地在杂乱中寻找规律。用数学的模型去拟合现实的数据，这就是统计。统计不像数学那么精确，统计的世界不是非黑即白的，它有“灰色地带”，但是统计会将理论与实际间的差别表示出来，也就是“误差”。

因此，统计世界中的公式会有一个小尾巴μ ，用来代表误差，即：

③损失函数

损失函数用来评判拟合函数的误差，损失函数越小，说明拟合函数越精准。

这个公式是残差平方和，在机器学习中它是回归问题中最常用的损失函数。现在我们知道了损失函数是衡量回归模型误差的函数，也就是我们要的“直线”的评价标准。这个函数的值越小，说明直线越能拟合我们的数据

④最小二乘估计

既然我们需要计算出拟合函数，即求出上述中的β0和β1。但是现在我们有很多点，且并不正好落在一条直线上，这么多点都能确定一条直线，这要怎么确定选哪条直线呢？这就用到了最小二乘法。最小二乘法中“二乘”是平方的意思。

普通最小二乘法给出的判断标准是：残差平方和的值达到最小。

⑤总结

所谓线性回归就是利用最小二乘法使得损失函数的值为最小值进而求出损失函数中的参数，又由于这里损失函数我们使用的是残差平方和，所以求出这里的损失函数的参数也就是拟合函数中的参数。所以确定了拟合函数

最后再提醒一点，做线性回归，不要忘了前提假设是y和x呈线性关系，如果两者不是线性关系，就要选用其他的模型啦。

1.2.2逻辑回归

逻辑回归

机器学习算法中的监督式学习可以分为2大类：

• 分类模型：目标变量是分类变量（离散值）

• 回归模型：目标变量是连续性数值变量

“分类”是应用逻辑回归的目的和结果，但中间过程依旧是“回归”。

①从线性回归讲起

最简单的情况下，只有一个自变量时，一元线性回归的拟合函数是一条连续直线。

而对于实际问题，因变量只有0、1两个取值，这种情况下如果执意使用线性回归函数进行拟合，则毫无意义。此时若使用加一条限制，在因变量的值大于某个值时使其为1，否则为0，这就拟合为了跃迁函数，如下所示：

但是跃迁函数并不是连续函数！！！理想的情况下我们应该用一个可导的函数来描述自变量和因变量之间的关系。因此引出了sigmond函数

②sigmond函数（逻辑函数的拟合函数）

逻辑回归算法的拟合函数，叫做sigmond函数：

函数图像如下（自变量为一元情况下）：

sigmoid函数是一个s形曲线，就像是阶跃函数的温和版，阶跃函数在0和1之间是突然的起跳。

sigmoid有个平滑的过渡。从图形上看，sigmoid曲线就像是被掰弯捋平后的线性回归直线，将取值范围(−∞,+∞)映射到(0,1) 之间，更适宜表示预测的概率，即事件发生的“可能性” 。

③推广多元场景下的拟合函数

由于多元线性回归方程的一般形式为：其中x和y都是列向量！

此形式可以简写为矩阵形式

其中，

将特征加权求和Xβ代入sigmond函数中的z，可以得到

④似然函数

概率(Probability) 来描述一个事件发生的可能性。

似然性(Likelihood) 正好反过来，意思是一个事件实际已经发生了，反推在什么参数条件下，这个事件发生的概率最大。

似然函数：表示模型参数中的似然性。

用数学公式来表达上述意思，就是

已知参数 β 前提下，预测某事件 x 发生的条件概率为P ( x ∣ β );

已知某个已发生的事件 x，未知参数 β 的似然函数为L ( β ∣ x ) ；

上面两个值相等，即: L ( β ∣ x ) = P ( x ∣ β ) 。

一个参数 β 对应一个似然函数的值，当 β 发生变化，L ( β ∣ x ) 也会随之变化。当我们在取得某个参数的时候，似然函数的值到达了最大值，说明在这个参数下最有可能发生x事件，即这个参数最合理。

因此，最优β，就是使当前观察到的数据出现的可能性最大的β。

⑤最大似然估计

最大似然估计

最大似然估计的理解：我们有一堆数据，我们为这一堆数据设计了一个模型。最大似然估计就是求可以使得模型最大可能得到这些数据时的参数

⑥损失函数

损失函数是用于衡量预测值与实际值的偏离程度，即模型预测的错误程度。这个值越小，认为模型效果越好，举个极端例子，如果预测完全精确，则损失函数值为0。

在线性回归一文中，我们用到的损失函数是残差平方和SSE：

这是个凸函数，有全局最优解。

如果逻辑回归也用平方损失，那么就是：

很遗憾，这个不是凸函数，不易优化，容易陷入局部最小值，所以逻辑函数用的是别的形式的函数作为损失函数，叫对数损失函数（log loss function）。

这个对数损失，就是上一小节的似然函数取对数后，再取相反数哟：

1.2.4决策树

决策树

①决策树概述

决策树是一种树形结构，每一个内部节点表示一种属性的测试，每一个分支表示一个测试输出，每个叶子节点表示一种类别。

根节点：第一个选择点

非叶子结点与分支：中间过程

叶子节点：最终的决策结果

那么决策树是怎么构建的呢？即怎么确定每一步划分时属性的选择呢？判断的依据是什么，在上图中根节点的属性判断就是outlook

②熵的作用

熵：表示随机变量不确定性的度量，用人话讲就是物体内部的混乱程度。

作用：我们可以计算出根据不同属性进行分支选择前后的熵值变化，进而从中选出最适合作为根节点，通过熵值的减少程度判断此次决策树的好坏

一般情况下熵值的计算是使用判断公式：

将分类后的每种类别的熵值之和与分类前的熵值进行比较，若小于分类前则说明分类较好，比原来有进步

③决策树的构造实例

这里使用官网提供的示例数据进行讲解，数据为14天打球的情况（实际的情况）；特征为4种环境变化（x i ）；最后的目标是希望构建决策树实现最后是否打球的预测（yes|no），数据如下

x 1：outlook

x 2 : temperature

x 3 : humidity

x 4 : windy

play：yes|no

由数据可知共有4种特征，因此在进行决策树构建的时候根节点的选择就有4种情况，如下。那么就回到最初的问题上面了，到底哪个作为根节点呢？是否4种划分方式均可以呢？因此 信息增益 就要正式的出场露面了

由于信息增益是需要判断决策前后的熵值变化，首先确定分类前的熵值，14天中9天打球，5天不打，所以此时的熵是

按照第一个特征值进行分类后的熵值

要注意并不是直接将每种情况的熵值直接想加，因为每种情况的发生概率是不一样的

这里就可以比较出熵值增益了，增益为0.247

这里再计算出另外三种情况下的增益，分别是temperature，humidity，windy。它们的值份别是0.029，0.152，0.048

我们选择增益最大的那个特征值，说明按照该特征值进行分类效果最好，故选择它。

④信息增益率和gini系数

但是有时候信息增益并不都适用，比如按照id（如果存在的话）进行分类时，此时熵值增益是最大的，但是按照id进行分类并不可行。

这里就发展出了另外的决策树算法——信息增益率和gini系数

比如还按照id进行分类，计算后的信息增益为Q=0.94，相较于其他四种分类方式属于较大值，这是信息增益率为

，利C4.5的情况下，虽然此时信息增益Q较大，但是此时分母也更大，所以这个公式计算出的信息增益率也就很小，解决了信息增益后无法处理分类后数据特别多的情况。

至于gini系数则是另起炉灶，有着自己的计算方式

⑤剪枝方法

为什么要剪枝操作？为了防止产生过拟合现象

剪枝策略：预剪枝（边建决策树边进行剪枝，比较实用）、后剪枝（当建立完成后再进行剪枝操作）

预剪枝方式：限制深度（比如指定到某一具体数值后不再进行分裂）、叶子节点个数、叶子节点样本数、信息增益量等

后剪枝方式：

1.2.5朴素贝叶斯

朴素贝叶斯

朴素贝叶斯例子

①介绍

朴素贝叶斯是经典的机器学习算法之一，也是为数不多的基于概率论的分类算法。原理简单，也很容易实现，多用于文本分类，比如垃圾邮件过滤。

②算法思想

逻辑回归通过拟合曲线（或者学习超平面）实现分类

决策树通过寻找最佳划分特征进而学习样本路径实现分类

支持向量机通过寻找分类超平面进而最大化类别间隔实现分类

朴素贝叶斯独辟蹊径，通过特征概率来预测分类。

③相关概念

贝叶斯公式

1.2.6K邻近KNN

KNN算法

①KNN算法简介

指导思想是”近朱者赤，近墨者黑“，即由你的邻居来推断出你的类别。

实现原理：为判断未知样本的类别，以所有已知样本作为参照，计算未知样本与所有已知样本的距离，从中选取与未知样本距离最近的K个已知样本，根据少数服从多数的投票法则（majority-voting），将未知样本与K个最邻近样本中所属类别占比较多的归为一类。

实际上K这个字母的含义就是要选取的最邻近样本实例的个数

举例：

②KNN算法实现的关键

（1） 样本的所有特征都要做可比较的量化

若是样本特征中存在非数值的类型，必须采取手段将其量化为数值。例如样本特征中包含颜色，可通过将颜色转换为灰度值来实现距离计算。

（2）样本特征要做归一化处理

样本有多个参数，每一个参数都有自己的定义域和取值范围，他们对距离计算的影响不一样，如取值较大的影响力会盖过取值较小的参数。所以样本参数必须做一些 scale 处理，最简单的方式就是所有特征的数值都采取归一化处置

（3）需要一个距离函数以计算两个样本之间的距离

通常使用的距离函数有：欧氏距离、余弦距离、汉明距离、曼哈顿距离等，一般选欧氏距离作为距离度量，但是这是只适用于连续变量。在文本分类这种非连续变量情况下，汉明距离可以用来作为度量。通常情况下，如果运用一些特殊的算法来计算度量的话，K近邻分类精度可显著提高，如运用大边缘最近邻法或者近邻成分分析法。

（4）确定K的值

K值选的太大易引起欠拟合，太小容易过拟合，需交叉验证确定K值。

③KNN算法的优缺点

优点：简单，无需训练；适合对稀有事件进行分类；适合多分类问题

缺点：

1.2.7学习向量量化

今天我将介绍一种和k-Means很相似的算法，叫做学习向量量化（Learning Vector Quantization）算法，这种算法也是希望通过寻找一组原型向量来刻画聚类的结构。这种“聚类”算法很奇特，它不再是无监督学习，而是一种需要预设标签的学习算法，学习过程通过这些监督信息来辅助聚类。

算法可以说是很清晰了，大白话来说，就是先选几个向量作为原型向量，然后在样本集中随机选取样本，计算和原型向量的距离，找出最邻近的原型向量，看看他们的标签是不是一样，一样的话原型向量向样本按照学习率靠拢，否则远离。就上面的过程，不断的迭代，直到满足迭代的停止条件。需要声明一点，这个迭代条件的设置有不同的方法，可以设置最大迭代轮次、也可以设置原型向量的更新阈值（如更新值很小就停止），需要根据需求设置。

LVD算法其实也是一种基于竞争的学习，这点和无监督的SOM算法挺像的。LVD算法可以被视为一种网络，由输入层、竞争层、输出层组成。输入层很容易理解，就是接受样本的输入；竞争层可以被视为神经元之间的竞争，也就是原型向量之间的竞争，离得最近的神经元（原型向量）获胜，赢者通吃（winner-take-all）；输出层负责输出分类结果。不论是如何理解这个算法，其实本质都是一样的，也就是同类靠拢、异类远离。

1.2.8支持向量机SVM

支持向量机

①概念

SVM全称是supported vector machine（⽀持向量机），即寻找到⼀个超平⾯使样本分成两类，并且间隔最⼤。是一种二类分类模型

用途：能够执⾏线性或⾮线性分类、回归，甚⾄是异常值检测任务。特别适用于中小型复杂数据集的分类

基本模型是在特征空间中寻找间隔最⼤化的分离超平⾯的线性分类器。

②支持向量机的分类

（1）线性可分支持向量机：训练样本线性可分时，通过硬间隔最大化，学习一个线性分类器。

（2）线性支持向量机：训练数据近似可分时，引入松弛变量，通过软间隔最大化，学习一个线性分类器

（3）非线性支持向量机：训练数据线性不可分时，通过使用核技巧及软间隔最大化。

1.2.9随机森林

决策树与随机森林

随机森林也是为了解决决策树的过拟合问题

随机森林的定义就出来了，利用bagging策略生成一群决策树的过程中，如果我们又满足了样本随机和特征随机，那么构建好的这一批决策树，我们就称为随机森林(Random Forest)。

1.2.10AdaBoost

①原理

是英文"Adaptive Boosting"（自适应增强）的缩写，它的自适应在于（1）前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一个基本分类器。（2）在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率或者是预先指定的最大迭代次数

1.2.11梯度提升算法

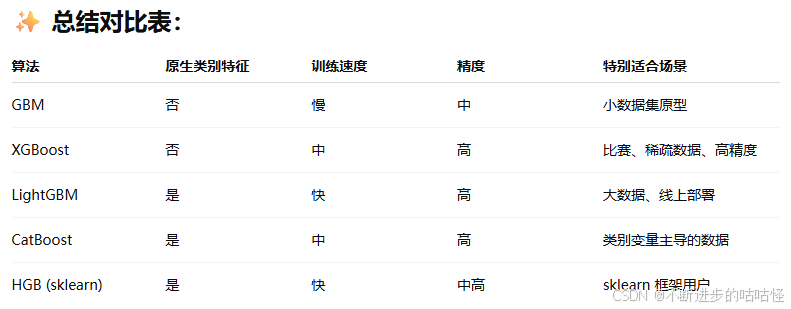
梯度提升算法是一种用于回归和分类问题的机器学习技术，它通过组合多个弱学习器（通常是决策树）来创建一个强学习器。这种方法通过在每一步迭代中加入一个新的模型来最小化损失函数（loss function），该新模型针对前序所有模型预测结果与实际值之间的误差进行优化。以下是几种常见的梯度提升算法：

1. Gradient Boosting Machine (GBM): 这是梯度提升的基础形式，通过使用任意可微分的损失函数来进行模型训练。

2. Stochastic Gradient Boosting: 是GBM的一种变体，它在每次迭代中随机抽样部分数据集进行训练，以此来提高模型的泛化能力，并减少过拟合的风险。

3. XGBoost (eXtreme Gradient Boosting): XGBoost是一个优化了的分布式梯度提升库。它实现了GBM的核心思想，但引入了正则化以控制模型复杂度，并采用了一些高级技巧如稀疏感知增益、并行化处理等，使其在速度和性能上都有显著改进。

   • min_child_weight：最小叶子节点样本权重和，控制过拟合；过大可能欠拟合，过小可能过拟合。假设你设置 min_child_weight=3，那么在分裂后，如果一个子节点只有两个样本（每个权重为 1），那么总和是 2，小于 3，就不会分裂。

   • gamma：分裂所需的最小增益（最小损失下降值）。分裂前后会计算一个“增益”（gain），即损失的下降值。如果增益小于 gamma，说明分裂带来的收益不大，XGBoost 就不会进行这个分裂。

4. LightGBM (Light Gradient Boosting Machine): 由微软开发，旨在提高大规模数据集上的训练速度和效率。它通过基于梯度的单边采样（GOSS）和互斥特征捆绑（EFB）等技术，能够更有效地处理高维度的数据。

5. CatBoost: 由俄罗斯搜索引擎Yandex开发，特别擅长处理类别型变量（categorical variables），它通过一种称为顺序贝叶斯优化的方法自动处理类别型特征，同时减少了预测偏移，提高了模型的质量。

这些算法各自有不同的特点和优势，选择哪一个取决于具体的应用场景、数据特性以及对计算资源的需求。

1.3非监督学习类

非监督学习中，给定的数据集没有“正确答案”，所有的数据都是一样的。无监督学习的任务是从给定的数据集中，挖掘出潜在的结构。例子：我们把一堆猫和狗的照片给机器，不给这些照片打任何标签，但是我们希望机器能够将这些照片分分类。

1.3.1高斯混合模型

1.3.2限制波尔兹曼机

1.3.3K-means聚类

Kmeans聚类

①Kmeans算法的原理和理解

Kmeans算法是最常用的聚类算法，主要思想是:在给定K值和K个初始类簇中心点的情况下，把每个点(亦即数据记录)分到离其最近的类簇中心点所代表的类簇中，所有点分配完毕之后，根据一个类簇内的所有点重新计算该类簇的中心点(取平均值)，然后再迭代的进行分配点和更新类簇中心点的步骤，直至类簇中心点的变化很小，或者达到指定的迭代次数。

②基本原理

假定给定数据样本X，包含了n个对象X = { X 1 , X 2 , X 3 , . . . , X n } ，其中每个对象都有m个属性。

Kmeans的目标是将n个对象依据对象间的相似性聚集到指定的k个类簇中，每个对象仅属于一个类簇。

步骤：

先初始化每个聚类中心，{ C 1 , C 2 , C 3 , . . . , C k } , 1 < k ≤ n ，然后计算每个对象到每一个聚类中心的欧式距离，欧式距离公式如下：

其中X i 表示第i个对象，C j 表示第j个聚类中心的1 ≤ j ≤ k ，t表示的是第几个属性。

再逐个比较每个对象到每一个聚类中心的距离，将对象分配到距离最近的聚类中心的类簇中，

得到k个类簇{ S 1 , S 2 , S 3 , . . . , S k }

1.3.4最大期望算法

1.4强化学习

强化学习更接近生物学习的本质，因此有望获得更高的智能。它关注的是智能体如何在环境中采取一系列行为，从而获得最大的累积回报。通过强化学习，一个智能体应该知道在什么状态下应该采取什么行为。最典型就是打游戏。2019年1月25日，AlphaStar（Google 研发的人工智能程序，采用了强化学习的训练方式） 完虐星际争霸的职业选手职业选手“TLO”和“MANA”

3深度学习算法(DL)

深度学习是机器学习的一个分支(最重要的分支)，机器学习是人工智能的一个分支。

深度学习领域的主要算法类型有：

1. 卷积神经网路CNN
2. 循环神经网络RNN
3. 长短期神经网络LSTM
4. 生成对抗网络GANs
5. 深度强化学习RL
6. 图神经网络GNN
7. Transformer

3.1卷积神经网-CNN

一文看懂卷积神经网络-CNN（基本原理+独特价值+实际应用）- 产品经理的人工智能学习库 (easyai.tech)

卷积神经网络与人类视觉处理的信息处理的原理相似，是逐层分级，逐层认知的。CNN的灵感来源就是人类视觉信息处理原理。

专为处理图像、音频等数据设计，广泛应用于图像识别、对象检测、语义分割等任务

主要组成部分：

• 输入层：将原始图像数据转换为网络输入；
• 卷积层：从局部区域提取特征并进行特征映射；
• 激活层：添加非线性，增强模型表达能力；
• 池化层：下采样特征图，保持尺度不变性和减少计算量；
• 归一化层：稳定训练过程，加速收敛；
• 全连接层：把特征图扁平化并通过权重矩阵进行分类或回归预测

知名的CNN算法：

LeNet-5（1990年代）主要用于手写数字识别任务；AlexNet（2012年）证明了深度学习在图像识别中的巨大潜力；VGG（2014）提高了图像分类的准确性；ResNet（Residual Networks）何凯明等人于2015年提出的残差网络解决了梯度消失问题；YOLO实现了实时的目标检测任务；U-Net用于医学图像分割任务；

3.2循环神经网络 – RNN

一文看懂循环神经网络 RNN（2种优化算法+5个实际应用） (easyai.tech)

专为处理序列数据设计的神经网络模型。

循环神经网络（Recurrent Neural Network, RNN）是一种专为处理序列数据设计的神经网络模型。它在传统的前馈神经网络（Feedforward Neural Networks）基础上引入了“循环”机制，使得信息可以从过去的时间步传递到未来的时间步，从而能够捕获和处理数据的时间依赖性。

在RNN中，每个时间步（timestep）的神经元会接收当前时刻的输入数据xt以及上一时刻隐藏层的输出ht-1作为输入，并计算出当前时刻的隐藏状态ht。隐藏状态ht可以看作是过去所有时间步输入信息的累积和压缩表示。其基本计算公式如下：

其中：

• xt​ 是当前时间步的输入；
• ht​ 是当前时间步的隐藏状态；
• Wax​ 和 Wah​ 分别是输入到隐藏层和隐藏层到隐藏层的权重矩阵；
• ba​ 是偏置项；
• g(⋅)是非线性激活函数，如tanh或ReLU等。

随后，当前时刻的隐藏状态ht会被用来计算输出yt，这一步通常会有一个独立的输出层，其计算公式可能类似于：

其中：

• y^​t​ 是对当前时间步输出的预测；
• Wyh​ 是从隐藏层到输出层的权重矩阵；
• by​ 是输出层的偏置项；
• 同样，g(⋅)在输出层可能是不同的激活函数，例如对于分类任务可能是softmax函数，而对于回归任务则可能不需要激活函数。

由于RNN具有这种记忆性结构，它们非常适合处理诸如文本序列（如句子）、语音信号和时间序列数据等各种时序数据，其中顺序是非常关键的特性。然而，在训练长序列时，RNN可能会遇到梯度消失/梯度爆炸问题，后来发展的长短时记忆网络（LSTM）和门控循环单元（GRU）等变体就是为了克服这些问题而设计的。

3.3长短期神经网络-LSTM（RNN的优化算法）

简要介绍一文看懂 LSTM - 长短期记忆网络（基本概念+核心思路） (easyai.tech)

举例解释通俗理解什么是 LSTM 神经网络 (qq.com)

①RNN和LSTM的区别

RNN 是一种死板的逻辑，越晚的输入影响越大，越早的输入影响越小，且无法改变这个逻辑。

LSTM做的最大的改变就是打破了这个死板的逻辑，而改用了一套灵活了逻辑——只保留重要的信息。

简单说就是抓重点。

②LSTM中的链式重复模块

RNN中这个模块比较简单， 例如只有单个tanh层

而LSTM的重复模块则有不同的结构

它通过引入遗忘门、输入门和输出门来控制信息的流动，从而能够有效地处理时间序列数据中的长期依赖关系

• 遗忘门：决定哪些信息从单元状态中丢弃。
• 输入门：决定哪些新信息将存储在单元状态中。
• 输出门：决定从单元状态中读取多少信息来输出。

3.4生成对抗网络 – GANs

3.5深度强化学习-RL

3.6图神经网络-GNN

3.7迁移学习-Transformer