机器学习:梯度下降,次梯度,随机梯度下降
梯度下降(Gradient Descent)是机器学习中最常见的优化算法之一,广泛用于模型训练和参数优化。本篇博客介绍梯度下降的基本原理,并深入探讨 批量梯度下降(GD)、随机梯度下降(SGD) 及 次梯度方法(Subgradient Method) 的区别与应用。我们将分析不同算法在 收敛速度、计算成本、稳定性 等方面的表现,并结合实际案例,帮助读者理解如何选择最适合的优化策略,以应对不同的机器
1,概述
1.1,梯度下降法
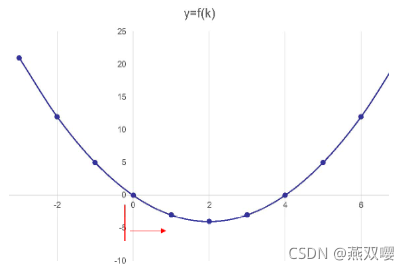
假定给定函数:
,求解该函数的极小值时,k的取值是多少?
通常做法:对
求导,然后令导数=0,求解 k 值即为所求:
1.2,迭代与梯度下降求解
求导解法在复杂实际问题中很难计算。迭代法通过从一个初始估计出发寻找一系列近似解来解决优化问题。其基本形式如下:
其中
被称为学习效率。
假设初始化
,为了通过迭代让
趋近最优解 2,
要满足两个条件:
要能使
向最优解逼近。
- 当
达到最优解时,
要等于0。当
达到最优解的时候,
要等于
,即:
因此,我们的核心问题:寻找
满足上述两个要求。
1.3,求解思路
随着迭代的不断进行,
可以使
向最优值逼近。而且,当
离最优值越近时,
的绝对值就越来越小。当达到最优解时,
。
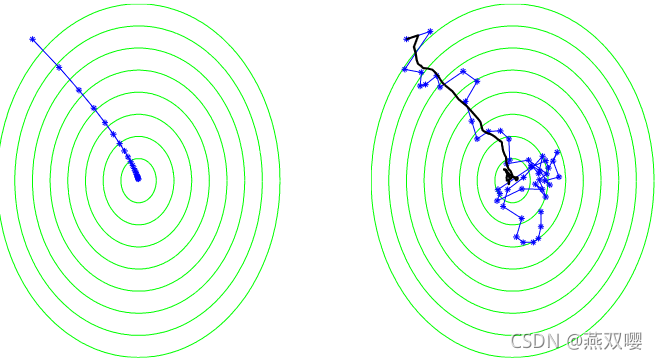
学习速率的取值问题:
- 当
取值较大时,即梯度下降迭代的步长较大,梯度下降迭代过程较快。可以快速迭代到最优解附近,但是可能一直在最优解附近徘徊,无法找出最优解。
- 当
取值较小时,即梯度下降迭代的步长较小,梯度下降迭代过程较慢。
梯度优化:方向+步长
2,梯度下降
2.1,可微函数的梯度
可微函数的梯度
:
在
处,
表示为是
的偏导数的向量,即:
梯度下降是一种迭代算法:
- 从初始值
开始。
- 在每次迭代中,沿着当前点梯度的负方向迈出下一步:
其中,
为学习率。直观地说,该算法在梯度点的相反方向上迈出了一小步,从而降低了函数的值。在
次迭代之后,算法输出最后一个向量
。
输出也可以是平均向量
。取平均值是非常有用的,特别是当我们将梯度下降推广到不可微函数和随机情况时。
【证明】
,即:梯度不断下降。
由于,
。
由于
,学习率
,所以
,故:
2.2,梯度下降算法的收敛速率
Lipschitz连续:对于在实数集的子集的函数
,若存在常数
,使得
,则称函数
符合利普希茨条件。
为了分析GD算法的收敛速度,我们仅限于凸 Lipschitz 函数的情况。
是
在
条件下的最小值的点坐标。
- 假设:
- 求证:
有界
2.3,凸函数性质
凸函数性质(1):
证明方法(1):
即,判断上述关系即可:
从图上可以看出,
,且趋近于0时取等号,不失一般性,可推广到其他凸函数上。
故,
凸函数性质(2):
证明:将
进行泰勒展开可得:
,且
处为偏导最小处,即
。
,且
处为偏导最小处,即
。
即:
即:Hessian矩阵
半正定,可以忽略非负项
故:
因此:
凸函数性质(1):
凸函数性质(2):
合体证明:
2.4,求解收敛速率
设
是向量的任意序列。任何具有初始化
和以下形式的更新规则的算法:
满足:
前提(1):
前提(2):
根据下一轮结果求和后一正一负抵消,可推出:
即:
特别的,对每个
,如果对所有的
都存在
使得
,且对每个
且
,都存在:
证明:由前面可得
令
则
,可得
得极小值,因此也是
的最小值。
且:
带入
可得:
当且仅当
在允许一定误差的情况下:对任意的
,使得:
则必须满足:
即:
,T 存在最小值。
3,次梯度
3.1,为何需要次梯度
次梯度方法是传统的梯度下降方法的拓展,用来处理不可导的凸函数。它的优势是比传统方法处理问题范围大,劣势是算法收敛速度慢。
对于光滑的凸函数而言,我们可以直接采用梯度下降算法求解函数的极值,但是当函数不处处光滑、处处可微的时候,梯度下降就不适合应用了。因此,我们需要计算函数的次梯度。对于次梯度而言,其没有要求函数是否光滑,是否是凸函数,限定条件很少,所以适用范围更广。
允许
是一个开凸集。
函数
是一个凸函数。满足下列条件的向量
:
称为
在
处的次梯度。
在
处的次梯度集称为微分集并表示为
。
3.2,计算次梯度
如果
在
处可微,那么
包含一个元素
在
处的梯度为
。
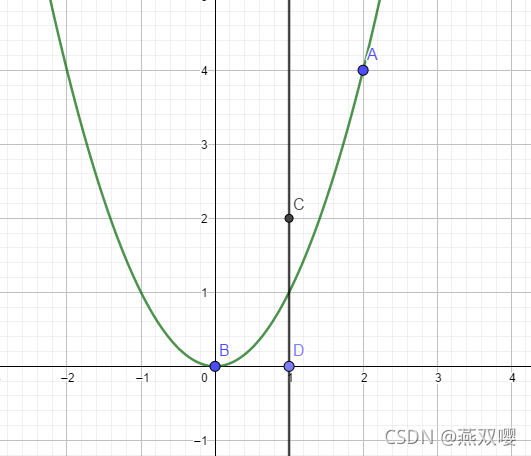
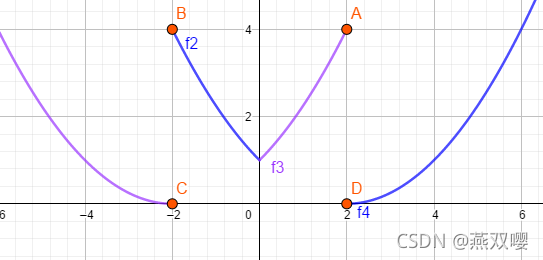
例如:
。
由于
在
处不可导,因此根据定义:

即:
求:
变换后得:
当取
时,
当取 0 时,
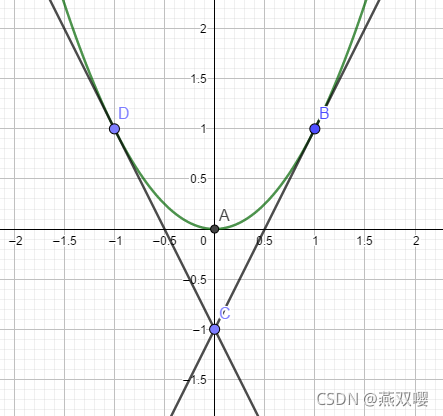
严谨写法:
令
关于
的凸可微函数
。存在某些
使得
,则
。
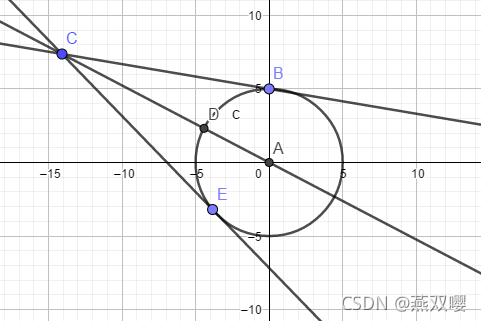
此时,取值C,D处作为次梯度点。
证明:
前提:
选择 C 作为次梯度点:
即,可得:
可得:
选择 B 作为次梯度点:
即,可得:
此时,
无解,故不可作为次梯度点。
4,随机梯度下降
4.1,核心思想
在随机梯度下降中,我们不要求更新方向完全基于梯度。相反,我们允许方向为随机向量,并要求其期望值为当前向量处函数的次梯度。
SGD伪码:在学习问题的背景下,很容易找到期望值为风险函数次梯度的随机向量。例如,每个样本的风险函数梯度。
4.2,使用SGD实现SVM
为了应用SGD,我们必须将上式中的优化问题转化为无约束问题:
更新规则:
一个次梯度为:
:在迭代
选择的随机例子上
处损失函数的次梯度。
,其中
为学习率。
4.3,SGD的收敛速度
特别的,对每个
,如果对所有的
都存在
使得
,且对每个
且
,都存在:
证明:
由2.3节证明的性质可得:
下面过程同2.4节,得:
带入,
故:
即证明:
同理,如果使得
都成立,则要求:
即:
,T 存在最小值。
4.4,投影步骤
在之前对GD和SGD算法的分析中,我们要求
,这相当于对
划定了一个半径为
的区间,然后进行选择。
但大部分时候我们无法保证全部的
的时候,可以采用增加投影的方法求解问题:
,不考虑范围求得一个值。
,然后投影到
上。
可以求得,D为最近的点,即投影点,B,E也是,但是不是最小的投影点。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容












所有评论(0)