深度学习之激活函数——Sigmoid
Sigmoid函数,又称logistic函数,是最早使用的激活函数之一。但是由于其固有存在的一些缺点,如今很少将其作为激活函数,但是依然常用于二分类问题中的概率划分。
·
Sigmoid激活函数
Sigmoid函数,又称logistic函数,是最早使用的激活函数之一。但是由于其固有存在的一些缺点,如今很少将其作为激活函数,但是依然常用于二分类问题中的概率划分。
函数表达式
sigmoid(x)=11+e−x sigmoid(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1
函数图像
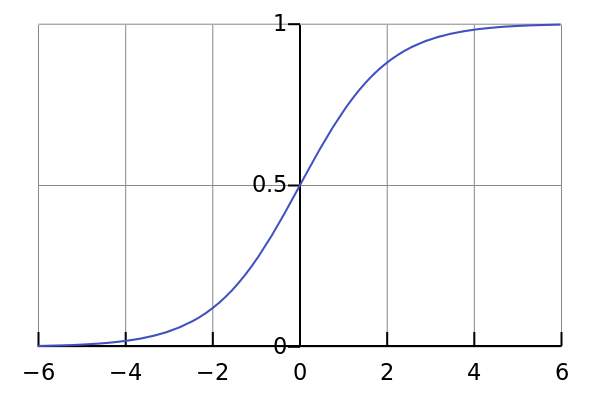
函数特性
优点:
-
sigmoid函数的输出范围限定在(0,1)(0,1)(0,1)之间,相当于做了归一化操作,可以用于将预测概率作为输出的模型
-
sigmoid梯度平滑,可以避免跳跃的输出值
-
sigmoid函数便于求导,计算量减小
求导公式为:f′(x)=f(x)[1−f(x)]f'(x)=f(x)[1-f(x)]f′(x)=f(x)[1−f(x)],可自行推导
缺点:
-
sigmoid函数容易饱和、出现梯度消失等问题。sigmoid函数只在原点附近有比较大的梯度变化,在两端梯度变化很小,参数难以更新。
我们不妨看一下其梯度图像:

不难发现其梯度只有在(−2,2)(-2,2)(−2,2)之间存在的比较大
-
sigmoid函数中出现指数运算,计算量较大。
注意这一步和之前的便于求导的优点并不冲突,因为即使其便于求导,在计算过程中也会遇到指数的运算。
于求导的优点并不冲突,因为即使其便于求导,在计算过程中也会遇到指数的运算。
- 函数图像不是关于原点中心对称的,这样会降低权重更新的效率
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容










所有评论(0)