线性回归

线性回归是线性模型中最经典的一种。线性模型一般用公式

来表示，其中

x是

线性模型具有很好的可解释性，譬如

就可以明显看出来

同时线性模型的优点还在于易于建模，形式简单。且很多非线性模型都可在线性模型的基础上通过引入层级结构或高维映射获得。

给定一个数据集D满足

其中每一个

线性回归要做的事情是将

使得

（PS：这个符号“渐进等于”，大致指左边可以连续变化到右边）

要想使得拟合呈现较高的水平，就得选择最适合的

均方误差。

其中

均方误差的公式对应了欧几里得距离（欧氏距离）。其公式在二维空间的表达如下：

基于均方误差最小化来进行模型求解的方法称作“最小二乘法”，最小二乘法的用途很广，不仅限于线性回归。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。下图是具有两个属性的Linear Regression优化的直观解释。

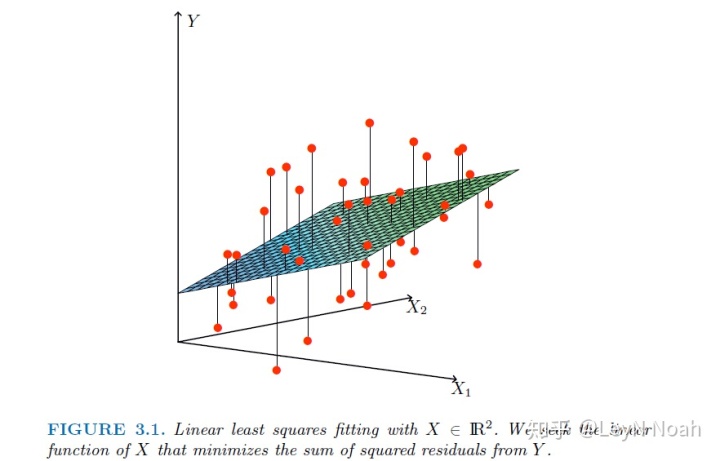
优化目标就是图中线段距离平方的均值，也就是最小化到分割平面的距离和。

求解

凸函数：对区间

衍生至多变量线性回归，求解过程类似，可得到

其中

最终学习到的线性回归模型为

如果求逆不好求的话可以不使用解析解，而是使用梯度下降等方式去求最优解。现实任务里

我们最后可以把线性回归模型简单的写成

如果我们假设输出标记其实是在指数尺度上变化，那就可将输出标记的对数作为线性模型逼近的目标，即

广义线性回归的参数估计通常都是通过加权最小二乘法或者极大似然估计进行。

关于使用极大似然估计推导线性回归的可以参考以下两篇文章：

极大似然，机器学习 --- 2. 从最大似然再看线性回归，

（参考：周志华《机器学习》，南瓜书，）