1、介绍

梯度下降法在机器学习中应用十分的广泛，它的主要目的是通过迭代搜索到目标函数的最小值；梯度下降法可以类比为一个下山的过程。假设，山上的雾非常大、可视度非常低、下山路径无法确定，而有一个人需要从山顶走到山谷（寻找目标函数的最小值），这个时候便可用梯度下降法来辅助下山。首先，以当前所处位置为基准寻找该位置最陡峭的方向，然后，朝着下降方向走一步。接着，又继续以当前位置为基准再寻找该位置最陡峭的方向，再朝着下降方向走一步。最后，重复该方法便可走到山谷；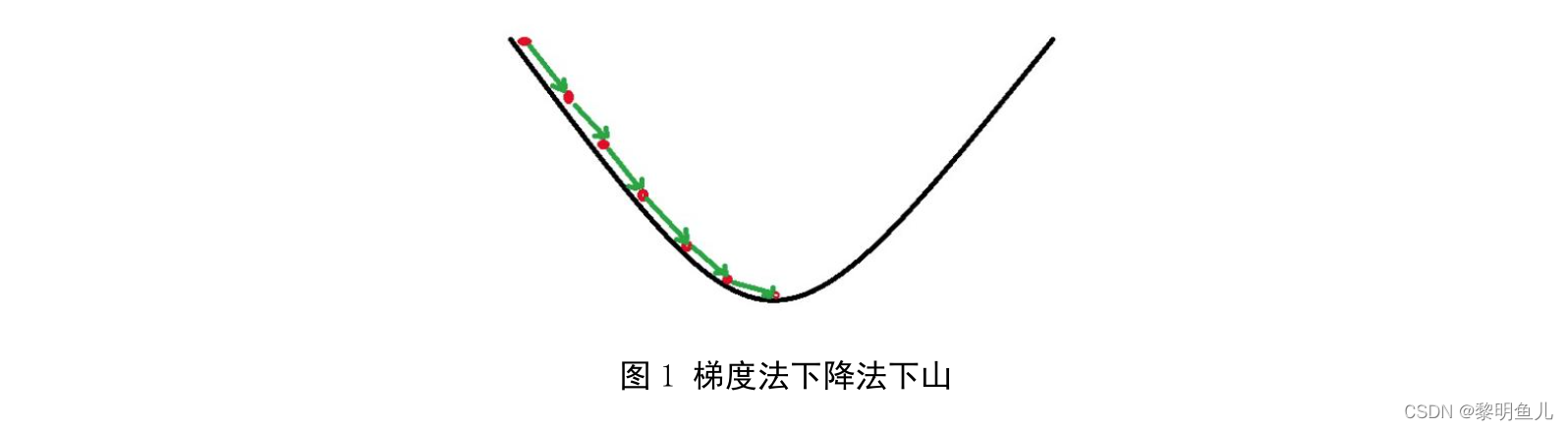

2、数学原理

目标函数$F(X)$在$X=X_k$处的不含皮亚诺余项的一阶泰勒公式如下:
$$F(X_k+\Delta X_k)\approx F(X_k)+\underset{F}{\underbrace{J(X_k)}}{}^T\Delta X_k(公式15)$$
通过公式 15 可推得:
$$G(\Delta X_k)\stackrel{\mathrm{def}}{=}F(X_k+\Delta X_k)-F(X_k)\approx \underset{F}{\underbrace{J(X_k)}}{}^T\Delta X_k(公式16)$$

该表达式中$F(X_k+\Delta X_k)$、$F(X_k)$是一个常数，$\underset{F}{\underbrace{J(X_k)}}{}^T$是一个常数矩阵，$\Delta X_k$是一个变量矩阵，即函数$G(\Delta X_k)$是以$\Delta X_k$为自变量的的一次函数。为了使$G(\Delta X_k)<0$恒成立（即：$F(X_k+\Delta X_k)<F(X_k)$），考虑到$\underset{F}{\underbrace{J(X_k)}}{}^T$和$\Delta X_k$是一个矩阵，所以可以借用向量性质来分析函数$G(\Delta X_k)$自变量和因变量之间的关系；
令：向量$\vec{A}=\underset{F}{\underbrace{J(X_k)}}{}^T$，向量$\vec{B}=\Delta X_k{}^T$，通过公式16可推得：
$$\begin{array}{rl}G(\Delta X_k)& \stackrel{\mathrm{def}}{=}\underset{F}{\underbrace{J(X_k)}}{}^T\Delta X_k\\ & =\vec{A}\cdot \vec{B}\\ & =|\vec{A}|\times |\vec{B}|\times \cos (\theta )\end{array}(公式17)$$
当向量$\vec{A}$和向量$\vec{B}$互为相反方向的时候公式17（$\eta$为步长）$G(\Delta X_k)<0$恒成立，可推得：
$$\vec{B}=-\eta \times \vec{A},s.t.(\eta >0)(公式18)$$
由公式 18 可推得：
$$\Delta X_k=-\eta \times \underset{F}{\underbrace{J(X_k)}}(公式19)$$
由公式 19 可推得目标函数$F(X)$的最优化迭代公式：
$$X_{k+1}\stackrel{\mathrm{def}}{=}{X}_k-\eta \times \underset{F}{\underbrace{J(X_k)}}(公式20)$$

3、Matlab程序

链接地址