本文主要给出三层神经网络前向推导的步骤和代码实现：

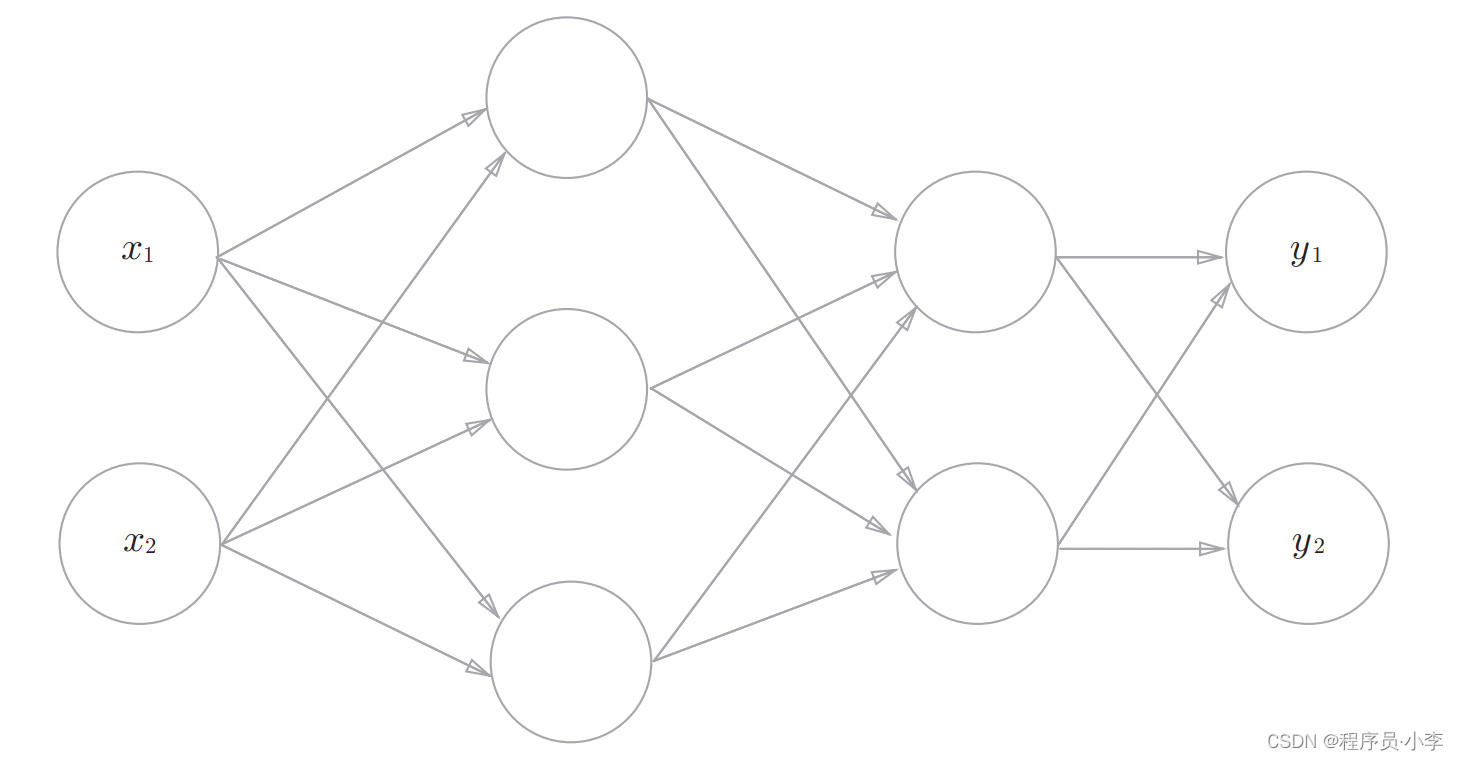
符号规定

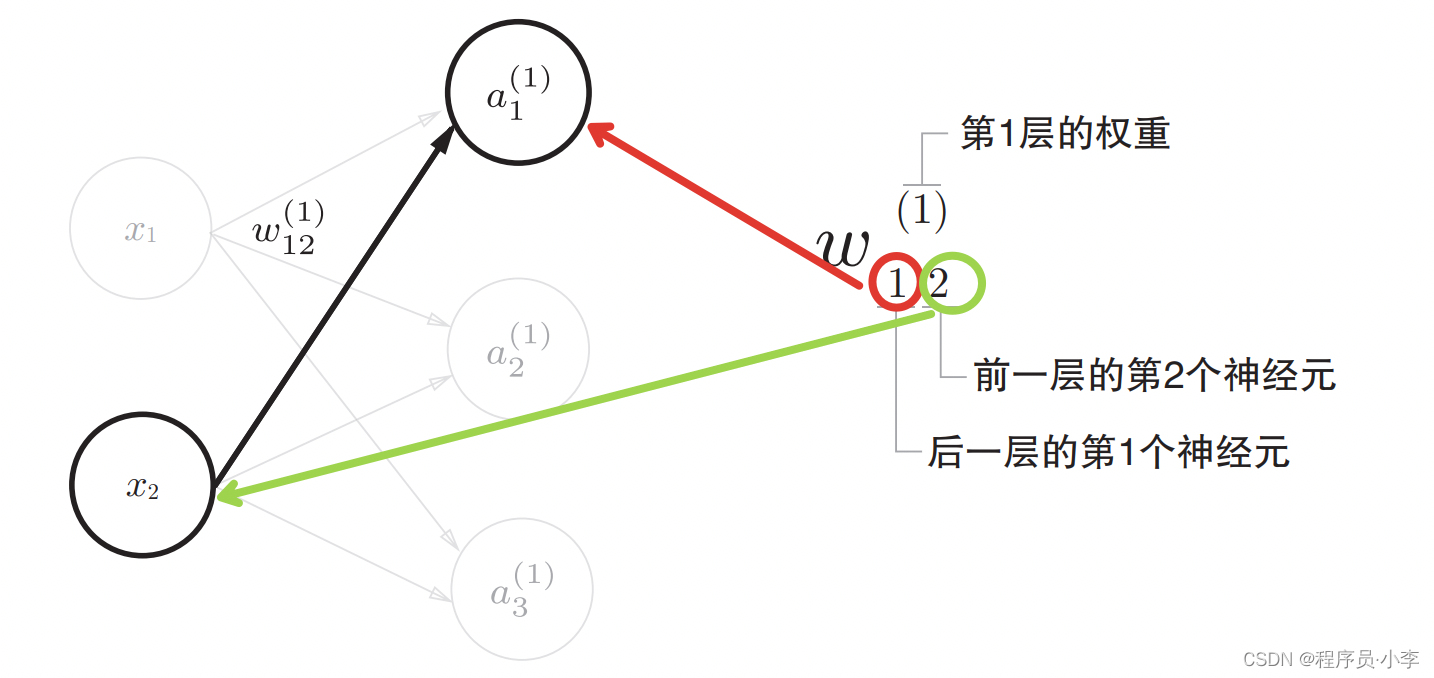
上述的符号表示为第一层神经元的权重，并且指定为前一层的2号神经元与后一层的1号神经元直接的权重。

第一层：输入层到第一隐藏层

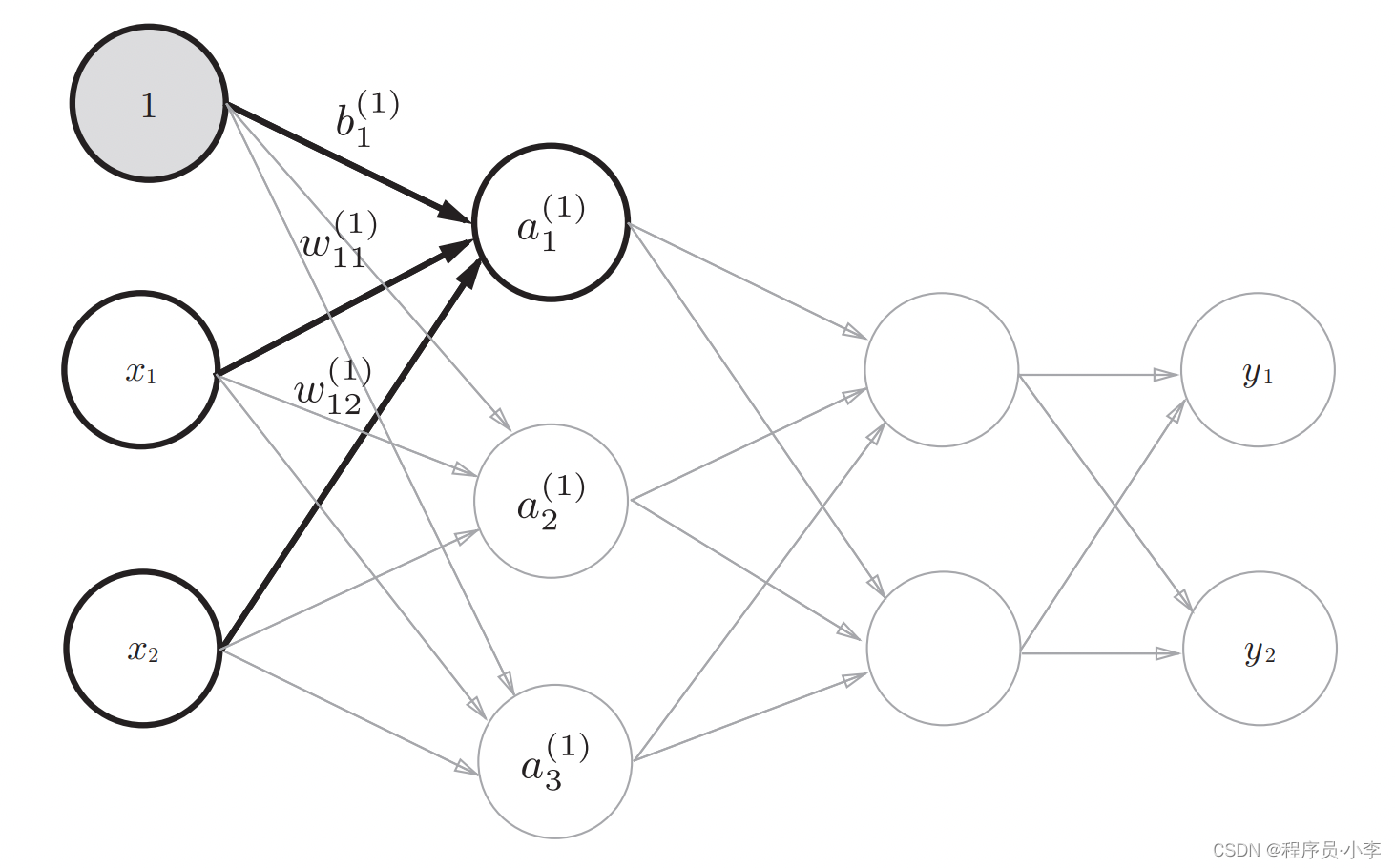
我们以a1为例，a1的值分为两个部分，一是权重与输入的乘积之和，二是偏置。

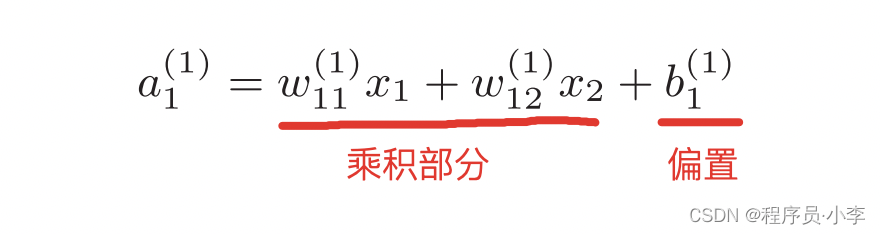
 以此类推，其实a2, a3的计算方法也是类似的

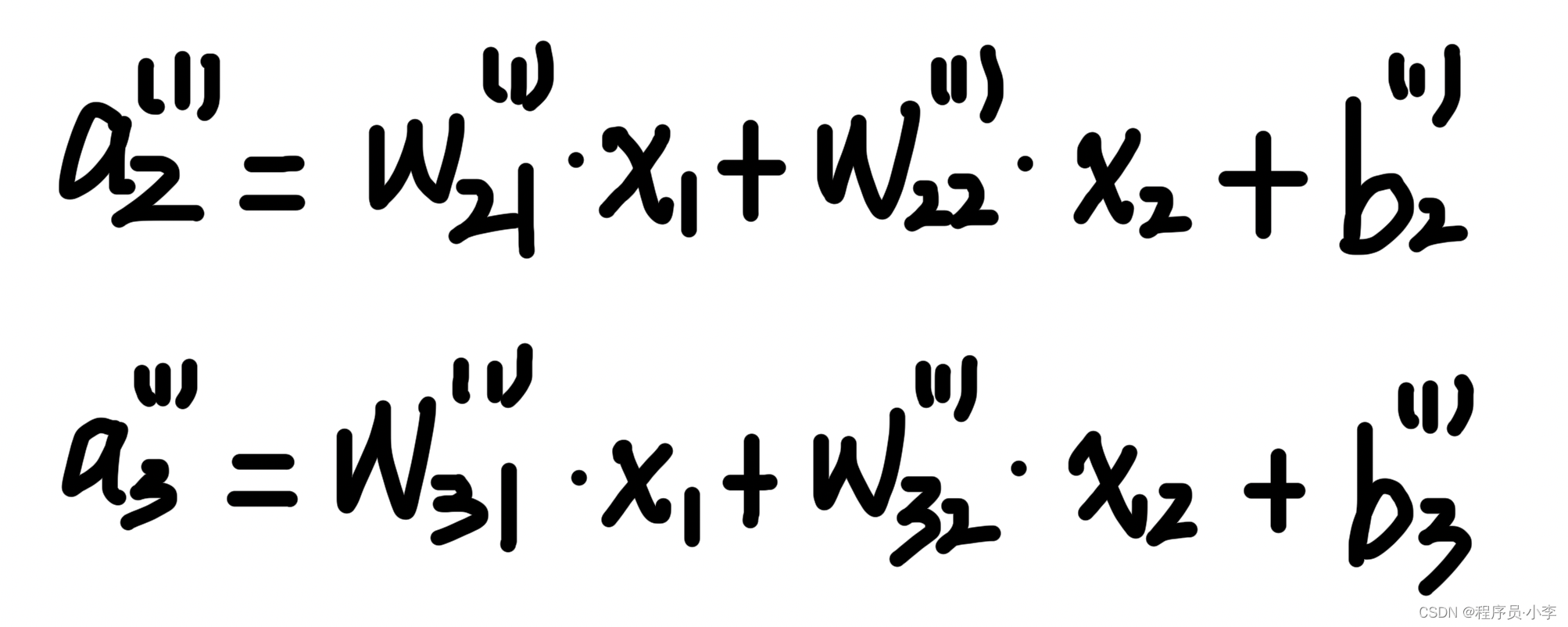
 我们用矩阵表示为：

 具体的矩阵：

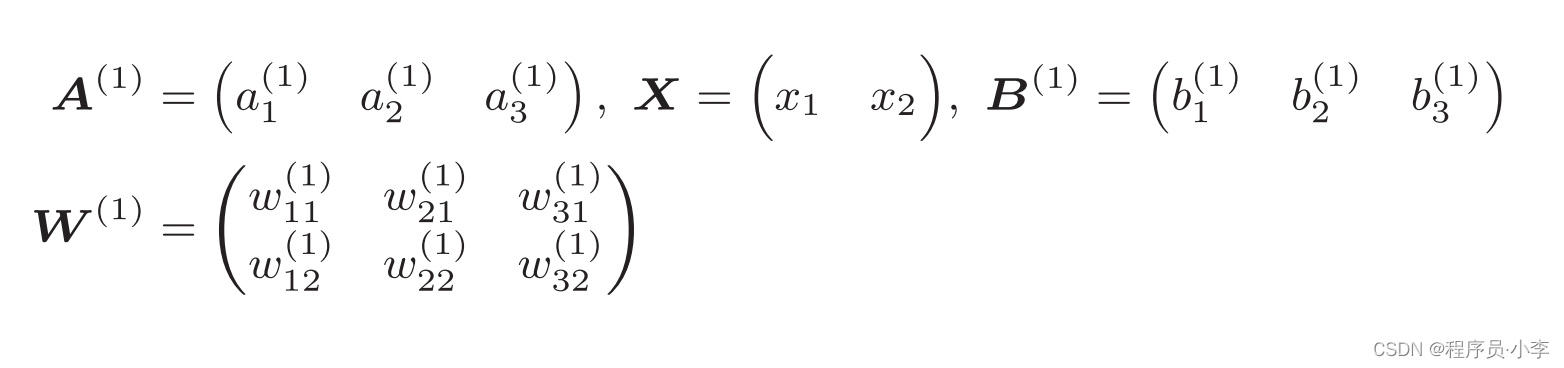
 代码实现A值计算：

X = np.array([1.0, 0.5]) # 输入矩阵
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) # 权重矩阵
B1 = np.array([0.1, 0.2, 0.3]) # 偏置矩阵

A1 = np.dot(X, W1) + B1

我们知道，A值计算出来后，需要使用激活函数进行激活：

Z1 = sigmoid(A1) # 使用SIGMOD激活

print(A1) # [0.3, 0.7, 1.1]
print(Z1) # [0.57444252, 0.66818777, 0.75026011]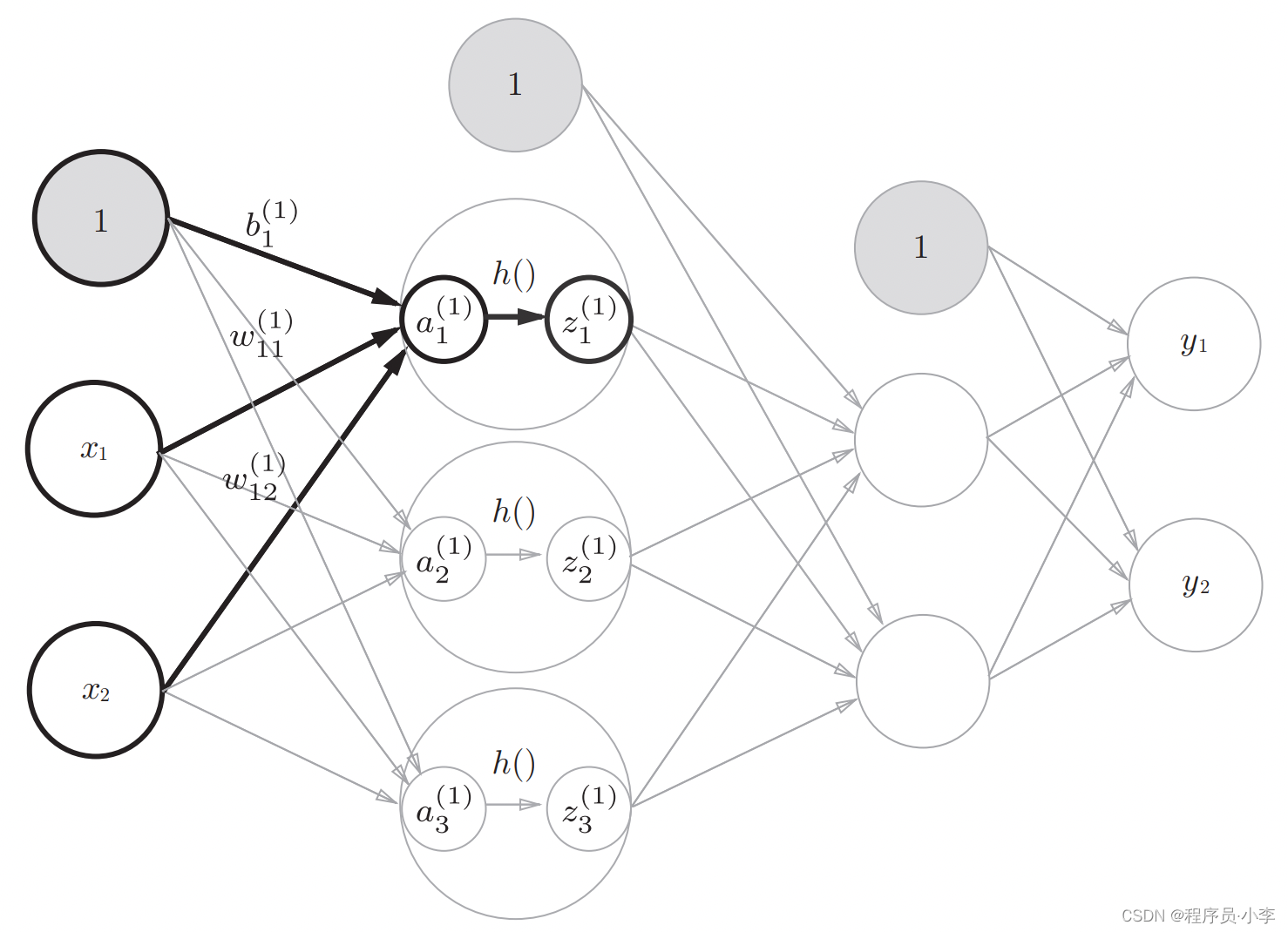

 整个输入层到第一隐藏层的计算就结束了。

1. 计算输入与权重乘积的和，加上偏置

2. 使用激活函数判断

第二层：第一隐藏层到第二隐藏层

与前一层的计算类似，

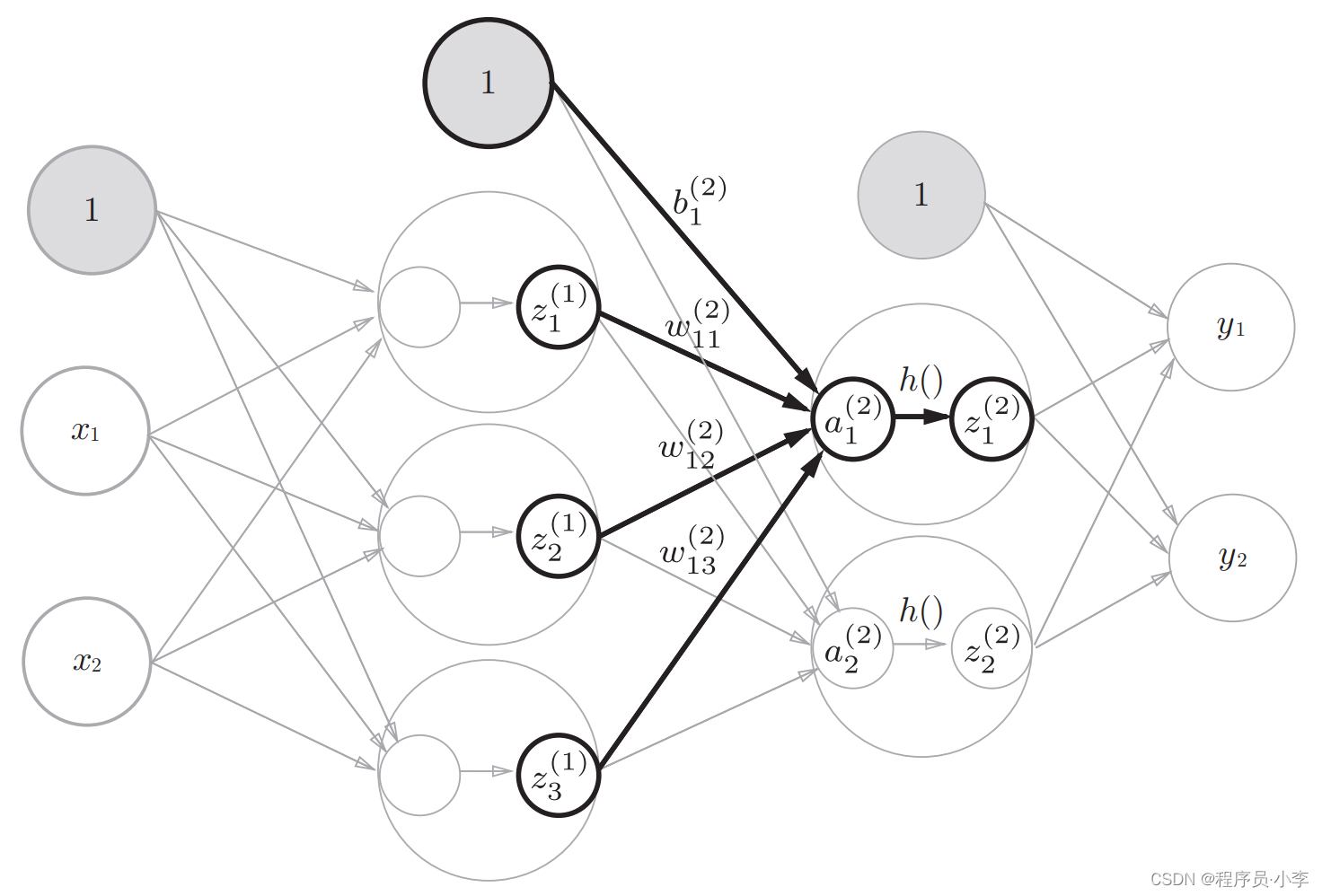
 先计算A

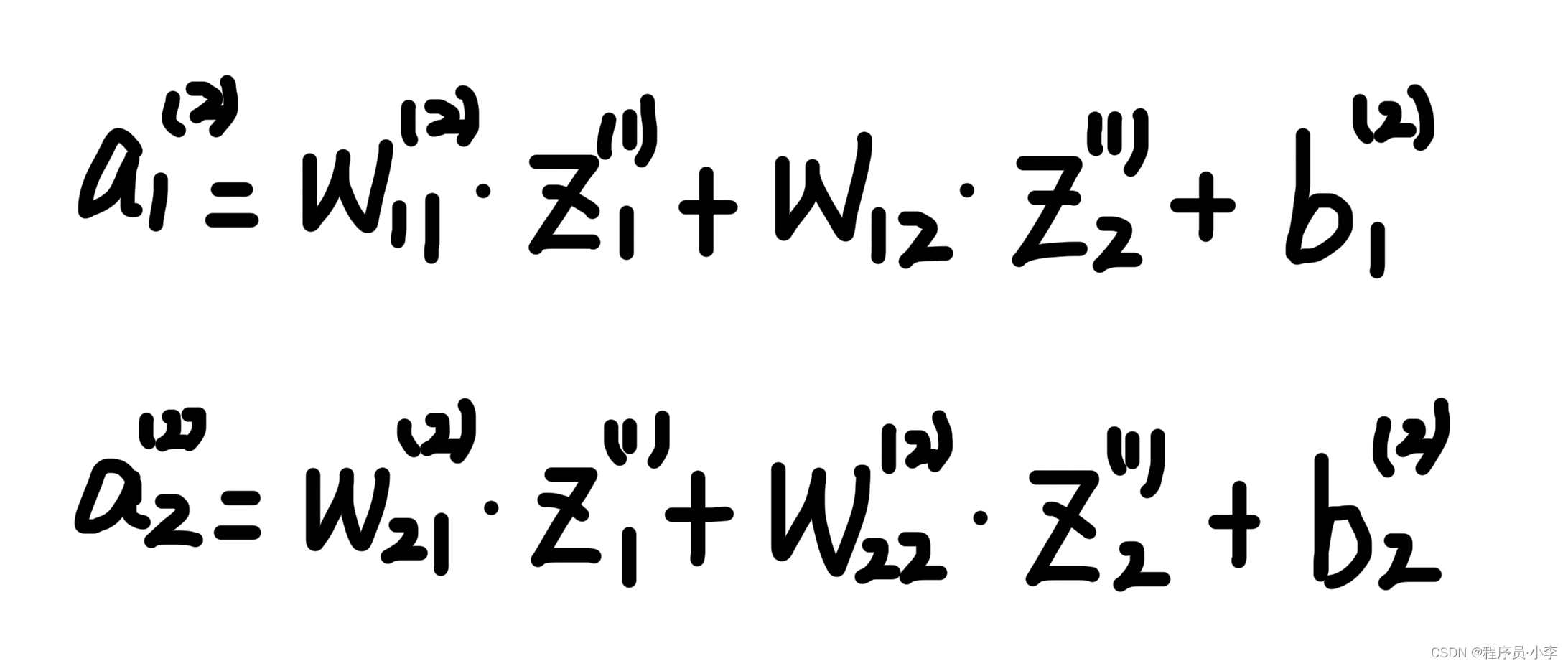
矩阵表示：

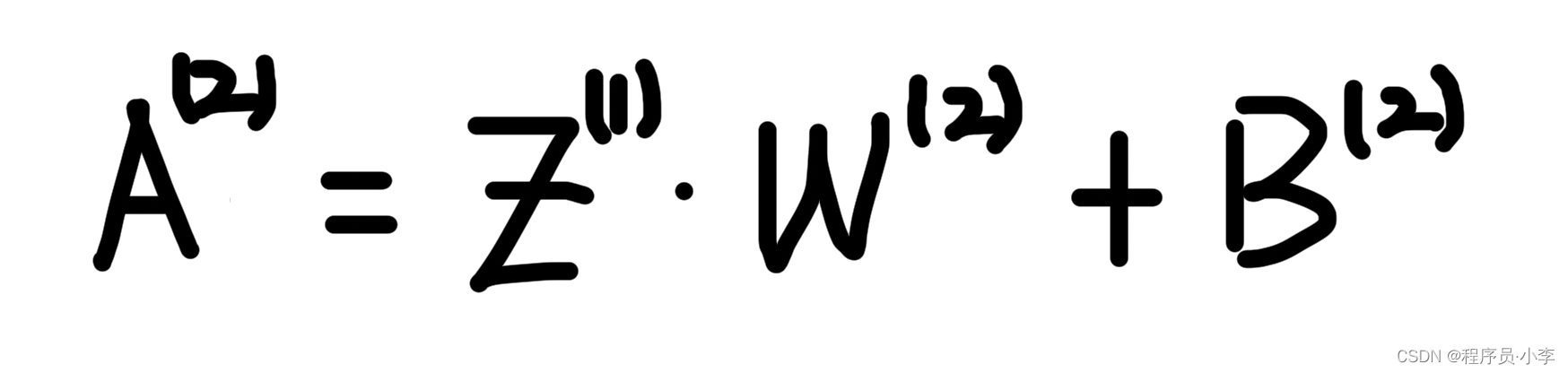
 代码实现：

W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) # 权重矩阵
B2 = np.array([0.1, 0.2]) # 偏置矩阵

A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

 

第三层：第二隐藏层到输出层

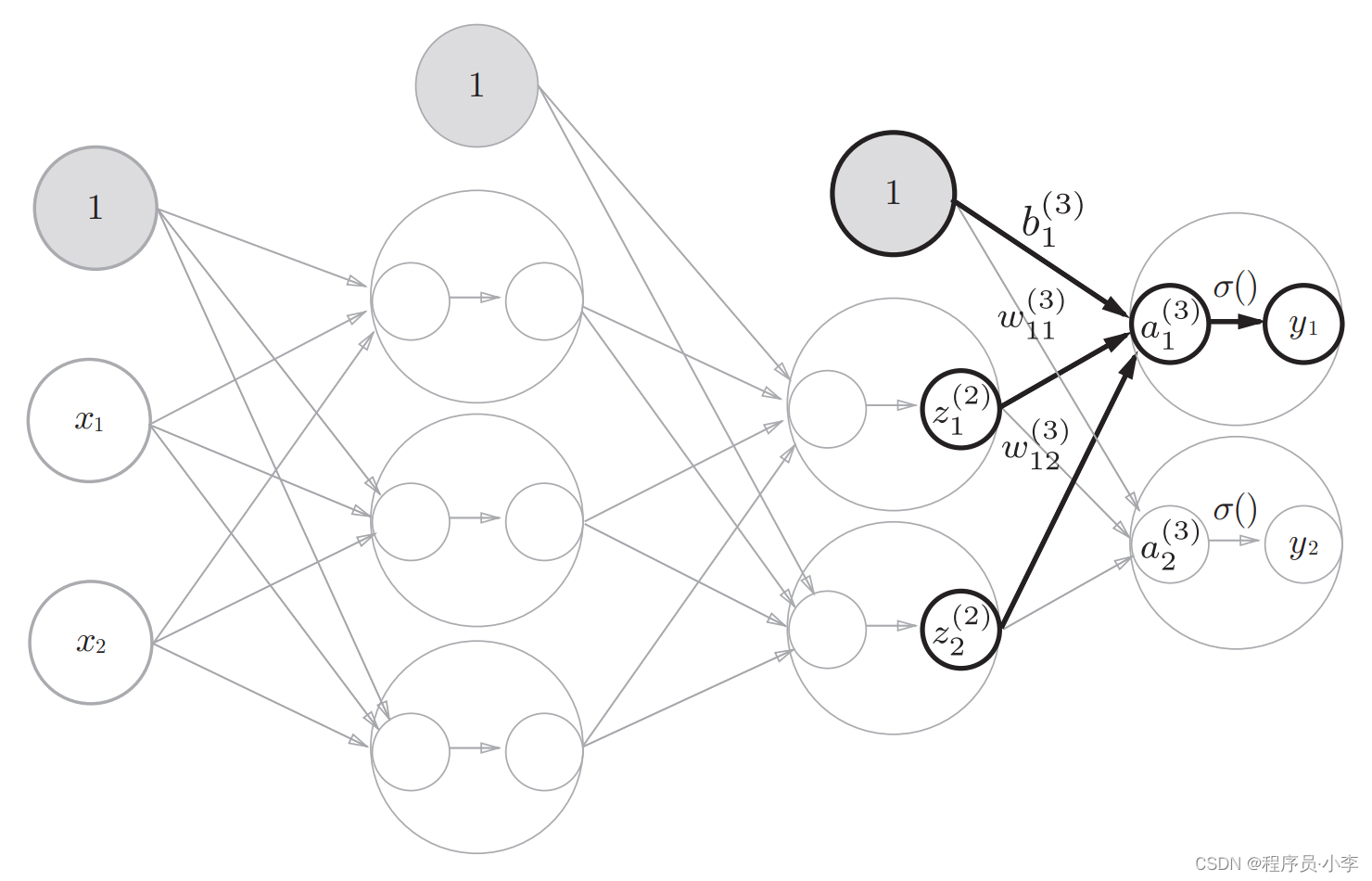
 与前两个步骤唯一不同的点在于，第三层的激活函数不再使用SIGMOD，而是采用的等值函数（原样输出y = x）

同样的，先计算A

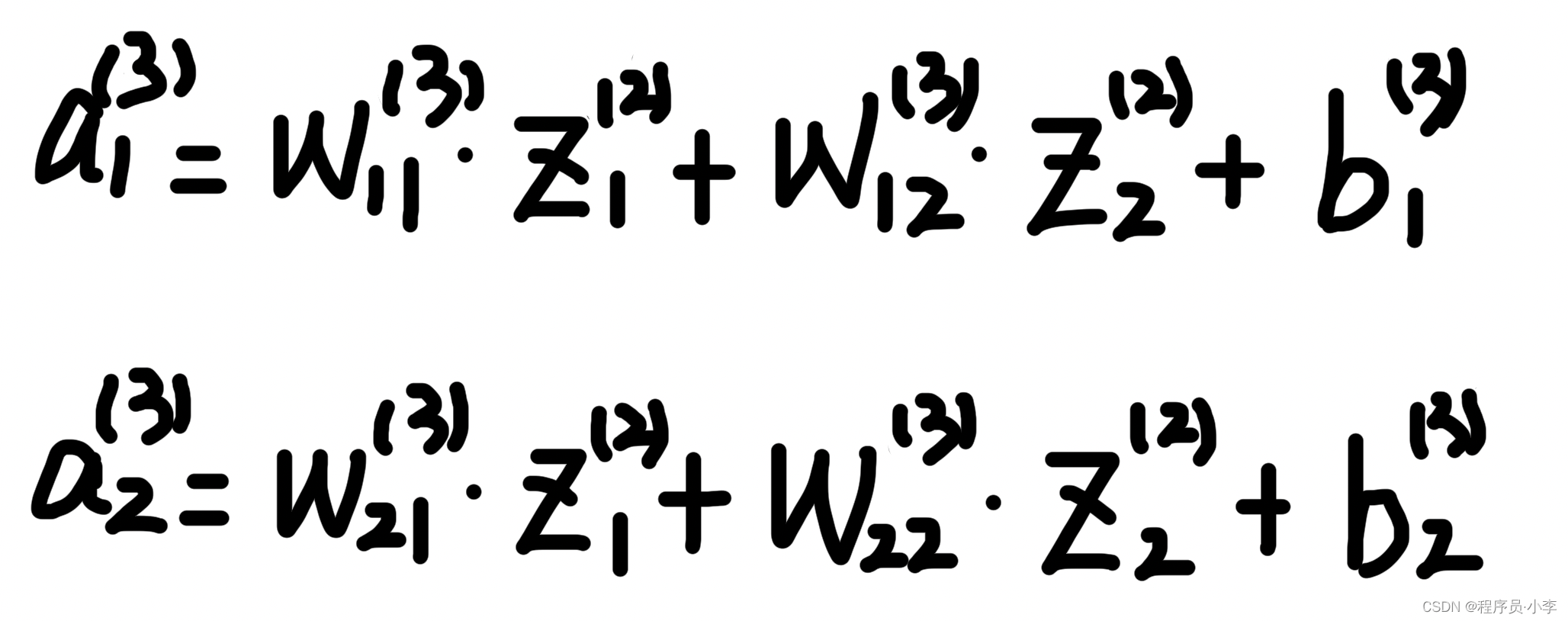
矩阵表示：

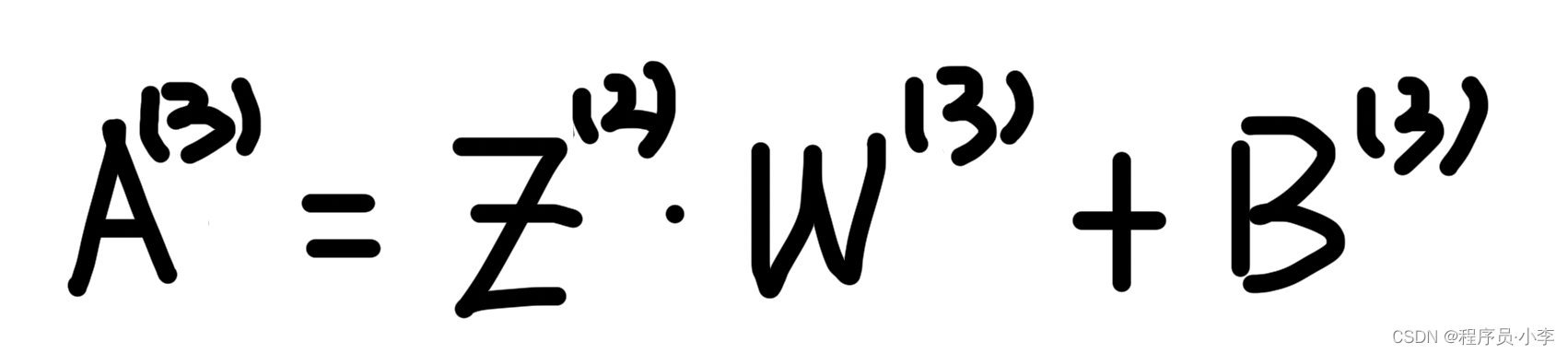
 代码实现：

def identity_function(x):
    return x

W3 = np.array([[0.1, 0.3], [0.2, 0.4]]) # 权重矩阵
B3 = np.array([0.1, 0.2]) # 偏置矩阵

A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3) # 或者Y = A3