信息论

信息论是应用数学的一个分支，主要研究的是对一个信号包含信息的多少进行
量化。它最初被发明是用来研究在一个含有噪声的信道上用离散的字母表来发送消息，例如通过无线电传输来通信。

在机器学习中，我们主要使用信息论的一些关键思想来描述概率分布或者量化概率分布之间的相似性。

熵的意义——信息量怎么度量？

信息论的基本想法是一个不太可能的事件居然发生了，要比一个非常可能的事件发生，能提供更多的信息。并且极端情况下，确保能够发生的事件应该没有信息量。

信息量可以被看成在学习某个事件X的值的时候的“惊讶程度”。如果有人告诉我们一个相当不可能的事件发生了，我们收到的信息要多于我们被告知某个很可能发生的事件发生时收到的信息。
​举个例子，消息说：‘‘今天早上太阳升起’’信息量是如此之少以至于没有必要发送，但一条消息说：‘‘今天早上有日食’’信息量就很丰富（发生概率小）。

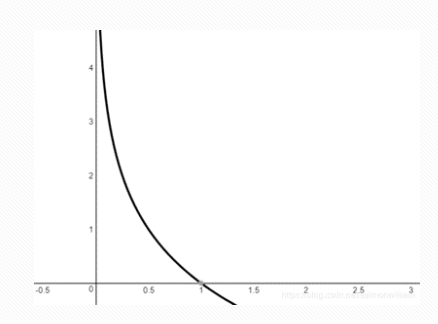
对于事件X的概率分布$p(x)$，我们想要寻找一个函数$h(x)$，是$p(x)$的单调递减函数，来表达信息的内容。

/>

香农定义了

$$h(x)=-\log P(x)\text{\hspace{1em}(1)}$$

对数的底决定信息量的单位。如果以2为底，信息量的单位记为比特（bit）；如果以e为底数，则信息量的单位记为奈特（nat）

那么熵$H(x)$定义为：

$$H(x)=-\sum _{x\in X}p(x){\log }_{2}p(x)=\sum _{x\in X}p(x)h(x)\text{\hspace{1em}(2)}$$

熵是随机变量X所有可能事件的自信息量的加权平均 ，所以熵又称为自信息（self-information），表示信源X每发一个符号（不论发什么符号）所提供的平均信息量。

熵的作用和认识

1. 熵(Entropy)—— Chaos（混沌），无序

2. 不确定性(Uncertainty)的衡量

   熵越高，不确定性越高，我们从一次实验中得到的信息量越大。正确估计其值的可能性就越小。

3. 熵值所代表的信息量的大小仅与不确定性有关，与信息的有效性或正确性无关。

   通常情况下，熵值越大，不确定性越高，我们从一次实验中得到的信息量越大，但其传递的信息中不确定性越大，有效信息反而越少，正确估计其值的可能性就越小。

以掷硬币为例：

• 若硬币均匀

  Ω = { H , T } \Omega=\{\mathrm{H}, \mathrm{T}\} Ω={H,T}
  $\mathrm{p}(\mathrm{H})=0.5,\mathrm{p}(\mathrm{T})=0.5$
  $\mathrm{H}(\mathrm{p})=-0.5{\log }_{2}0.5+\left(-0.5{\log }_{2}0.5\right)=1$

• 硬币稍微不均匀：

  $$p(H)=0.2,p(T)=0.8,H(p)=0.722$$

• 硬币非常不均匀：

  $$p(H)=0.01,p(T)=0.99,H(p)=0.081$$

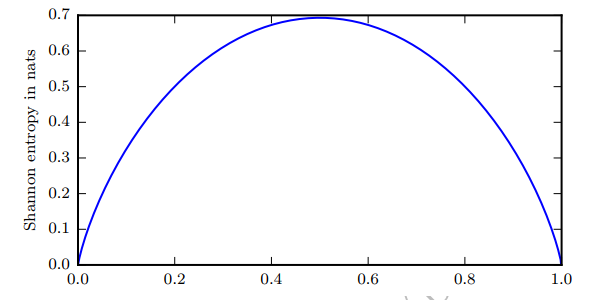
可以看到，熵值越大，不确定性越大，有效信息越少

那些接近确定性的分布 (输出几乎可以确定) 具有较低的熵；那些接近均匀分布的概率分布具有较高的熵。

/>

几种特殊的熵

1.联合熵

实际上就是描述一对随机变量平均所需要的信息量。

$$H(X,Y)=-\sum _{xerye}p(x,y){\log }_{2}p(x,y)\text{\hspace{1em}(3)}$$

2.条件熵

给定随机变量$X$的情况下，随机变量$Y$的条件熵定义：

$$\begin{array}{rl}H(Y\mid X)& =\sum _{x\in X}p(x)H(Y\mid X=x)\\ & =\sum _{x\in X}p(x)\left[-\sum _{y\in Y}p(y\mid x)\log p(y\mid x)\right]\\ & =-\sum _{x\in X}\sum _{y\in Y}p(x,y)\log p(y\mid x)\end{array}\text{\hspace{1em}(4)}$$

3.互信息

互信息$I(X;Y)$是在知道了$Y$的值后$X$的不确定性的减少量。即$Y$的值透露了多少关于$X$的信息量。

$$I(X;Y)=H(X)-H(X|Y)\text{\hspace{1em}(4)}$$

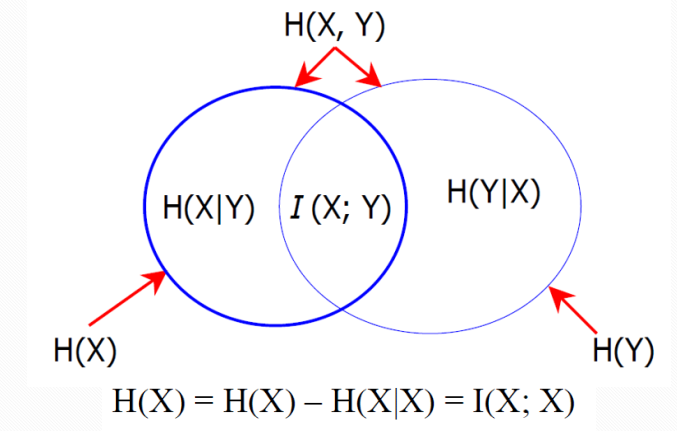
互信息、条件熵、联合熵的关系：

/>

特殊情况下，如果$H(X,X)=0$，那么$H(X)=H(X)-H(X|X)=I(X;X)$。

• 说明了为什么熵又被称为自信息

• 说明了两个完全相互依赖的变量之间的互信息并不是一个常量，而是取决于它们的熵

• 互信息体现了两变量之间的依赖程度：

  如果$I(X;Y)>>0$，表明$X$和$Y$是高度相关的
  如果$I(X;Y)=0$，表明$X$和$Y$是相互独立的
  如果$I(X;Y)<<0$，表明$X$和$Y$是互补相关的（高度不相关）

4.相对熵（KL散度）

如果我们对于同一个随机变量X有两个单独的概率分布P(X)和Q(X)。相对熵是用概率分布Q来近似另一个概率分布P时所造成的信息损失量。

$$D(p||q)=\sum _{x=x}p(x)\log \frac{p(x)}{q(x)}\text{\hspace{1em}(5)}$$

假设一个问题中，在机器学习中： $P=[1,0.0]$，是样本的真实分布，表示当前样本属于第一类，$Q[0.7,0.2,0.1]$用来表示模型所预测的分布。如果用P来描述样本完全反映了真实分布。而用Q来描述样本，虽然可以大致描述，但是不是那么的准确，信息量不足，需要额外的一些“信息增量”才能达到和P一样准确的描述。

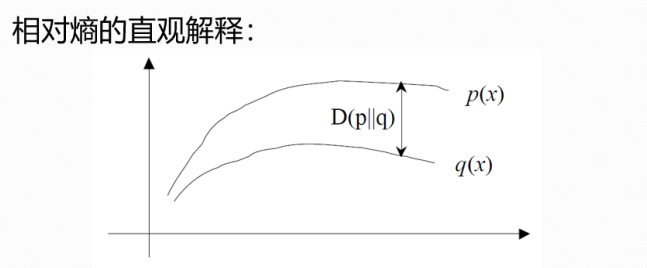
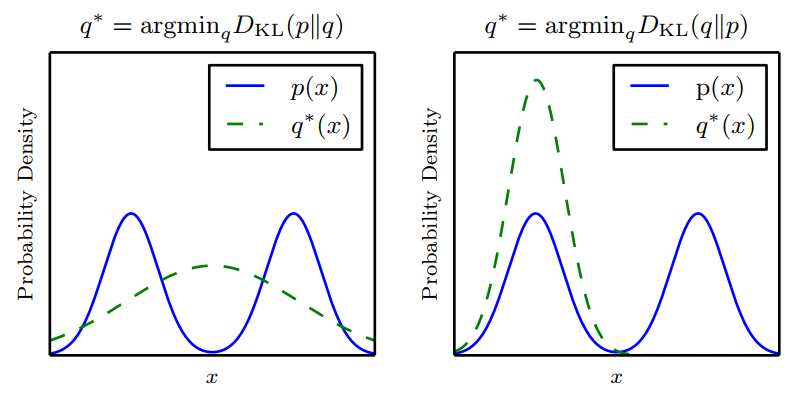
所以说，KL散度反映了两个分布的差异性。然而，它并不是真的距离因为它不是对称的：对于某些 P 和 Q， $D_{KL}(P||Q)\ne D_{KL}(Q||P)$。这种非对称性意味着选择$D_{KL}(P||Q)$还是 $D_{KL}(Q||P)$影响很大。

/>

5.交叉熵(cross entropy)

对交叉熵进行变形：

$$\begin{gathered} D_{KL}(p\Vert q)=\sum _{i=1}^{n}p\left(x_i\right)\log \left(\frac{p\left(x_i\right)}{q\left(x_i\right)}\right) \\ =\sum _{i=1}^{n}p\left(x_i\right)\log p\left(x_i\right)-\sum _{i=1}^{n}p\left(x_i\right)\log q\left(x_i\right) \\ =-H(p(x))+\left[-\sum _{i=1}^{n}p\left(x_i\right)\log q\left(x_i\right)\right] \end{gathered}$$

如果一个随机变量$Xp(x)$，$q(x)$为用于近似$p(x)$的概率分布，那么随机变量X和模型$q$之间的交叉熵定义为：

$$\begin{gathered} H(X,q)=H(X)+D(p||q) \\ =-\sum _X^{\ast }p(x)\log q(x) \\ =E_p(\log \frac{1}{q(x)})\text{\hspace{1em}(6)} \end{gathered}$$

即根据q分布，对p进行编码需要的bit数（交叉熵）

交叉熵的作用：在在很多机器学习任务中，我们需要评估真实答案$label\in p(x)$和模型预测结果$predicts\in q(x)$之间的差距。
评估时，显然需要用KL散度进行度量，但KL散度里$H(p(x))$是不变的，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用交叉熵做损失函数，评估模型

注：当我们计算以上这些量时，经常会遇到 $0log0$这个表达式。按照惯例，在信息论中，我们将这个表达式处理为${\lim }_{x\to 0}x\log x=0$