接着上一回继续讲【计算机视觉基础】1.矩阵的作用_mjiansun的博客-CSDN博客

1.齐次坐标和齐次坐标系的引入

前面有个问题我们还没聊开，不知道小伙伴们记得不？在几何向量的基本概念这一章，我们了解了如下两个概念：

        1.矢：空间中的一个直线段，当规定其两个端点中一个为起始点，一个位终止点，这个线段就称为一个矢。

        2.向量：具有同样长度和方向的矢的集合称为一个向量，单独的一个矢为向量的一个代表。

        这里就引出了我们迷惑的问题了，因为数学上（当然程序中也一样）表示向量和坐标点是一样的，比如向量a = (3,2,5)，坐标点P = (3,2,5)，这也就罢了，然而向量a = (3,2,5)可以表示空间中平行且长度相同的任意向量。

为了区分向量和点引入了齐次坐标和齐次坐标系。为了方便说明，对于一个向量v以及基oabc，可以找到一组坐标(v1,v2,v3)，使得

v = v1 a + v2 b + v3 c          （1）

而对于一个点p，则可以找到一组坐标（p1,p2,p3），使得

p – o = p1 a + p2 b + p3 c            （2），

        从上面对向量和点的表达，我们可以看出为了在坐标系中表示一个点（如p），我们把点的位置看作是对这个基的原点o所进行的一个位移，即一个向量——p – o（有的书中把这样的向量叫做位置向量——起始于坐标原点的特殊向量），我们在表达这个向量的同时用等价的方式表达出了点p：

p = o + p1 a + p2 b + p3 c (3)

        (1)(3)是坐标系下表达一个向量和点的不同表达方式。这里可以看出，虽然都是用代数分量的形式表达向量和点，但表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达(1, 4, 7)，谁知道它是个向量还是个点！

    我们现在把（1）（3）写成矩阵的形式：

v = (v1 v2 v3 0) X (a b c o)

p = (p1 p2 p3 1) X (a b c o),

        这里(a,b,c,o)是坐标基矩阵，右边的列向量分别是向量v和点p在基下的坐标。这样，向量和点在同一个基下就有了不同的表达：3D向量的第4个代数分量是0，而3D点的第4个代数分量是1。像这种这种用4个代数分量表示3D几何概念的方式是一种齐次坐标表示。

        这样，上面的(1, 4, 7)如果写成（1,4,7,0），它就是个向量；如果是(1,4,7,1)，它就是个点。下面是如何在普通坐标(Ordinary Coordinate)和齐次坐标(Homogeneous Coordinate)之间进行转换：

(1)从普通坐标转换成齐次坐标时

   如果(x,y,z)是个点，则变为(x,y,z,1);

   如果(x,y,z)是个向量，则变为(x,y,z,0)

(2)从齐次坐标转换成普通坐标时   

   如果是(x,y,z,1)，则知道它是个点，变成(x,y,z);

   如果是(x,y,z,0)，则知道它是个向量，仍然变成(x,y,z)

        以上是通过齐次坐标来区分向量和点的方式。从中可以思考得知，对于平移T、旋转R、缩放S这3个最常见的仿射变换，平移变换只对于点才有意义，因为普通向量没有位置概念，只有大小和方向.

        而旋转和缩放对于向量和点都有意义，你可以用类似上面齐次表示来检测。从中可以看出，齐次坐标用于仿射变换非常方便。

        由于齐次坐标使用了4个分量来表达3D概念，使得平移变换可以使用矩阵进行，从而如F.S. Hill, JR所说，仿射（线性）变换的进行更加方便。由于图形硬件已经普遍地支持齐次坐标与矩阵乘法，因此更加促进了齐次坐标使用，使得它似乎成为图形学中的一个标准。

1.1 齐次坐标具体定义

齐次坐标是一个相机标定问题的关键理论之一，所以就此问题分析一下。
单从定义上来讲，齐次坐标（投影坐标）就是用N+1维来代表N维坐标（点和向量），也可说用齐次坐标来表示笛卡尔坐标，具体的数学表达式可以这样写：
在直角坐标系点坐标（x,y）末尾加上一个额外的变量w，一个点(X,Y)在齐次坐标里面变成了（x,y,w），并且有

X = x/w
Y = y/w

这也就解决了笛卡尔坐标系无法表示无穷远点的问题，按照人的视觉，两条平行线在无穷远处会相交，采用直角坐标系无法对这一现象进行描述，而当w趋近于0时，(X,Y)趋向无穷大，其齐次坐标就可表示为(x,y,0)，解决了这一问题。

于此同时衍生了另外一个问题，笛卡尔坐标和齐次坐标转换的问题：
(1) 笛卡尔坐标转换成齐次坐标，需要考虑坐标是点还是向量的问题，如果(x,y)是个点，就可变为(x,y,1)；而如果(x,y)是个向量，则变为(x,y,0)
(2) 齐次坐标转换成笛卡尔坐标，如果是(x,y,2)，则其笛卡尔坐标为(x/2,y/2);
如果是(x,y,0)，其笛卡尔坐标仍为(x,y)。
齐次坐标（针对二维）因此有如下定义：

1. 投影平面上的任何点都可以表示成 (X, Y, Z)，称之为该点的’齐次坐标或投影坐标，其中 X、Y 及 Z 不全为 0。
2. 以齐次坐标表表示的点，若该坐标内的数值全乘上一相同非零实数，仍会表示该点。
3. 相反地，两个齐次坐标表示同一点，当且仅当其中一个齐次坐标可由另一个齐次坐标乘上一相同非零常数得取得。
4. 当 Z 不为 0，则该点表示欧氏平面上的 (X/Z, Y/Z)。
5. 当 Z 为 0，则该点表示一无穷远点。
6. 三元组 (0, 0, 0) 不表示任何点。原点表示为 (0, 0, 1)。

1.2 齐次坐标系

那怎么从空间上去理解齐次坐标系呢？

有个说法挺有意思，我们想象在宇宙中有一个绝对坐标系，对于我们现在使用的笛卡尔坐标系，其原点位于(0,0)点，当然同时也就还有无数的相同的坐标系，只不过它们的原点不同，对于笛卡尔坐标系中的点（x,y），它对于所有的笛卡尔坐标系都是相同的，有点多维宇宙的感觉，其中一个坐标系就是一个宇宙。

2. 齐次坐标的附带功效

2.1 空间几何和笛卡尔空间坐标系

        笛卡尔和费马两人创立了解析几何，我们前面也说过几何学一开始就是为了测量大地的，所以有平面几何以及笛卡尔平面坐标系，测量大地后当然也就要去测量天空和大海了，就有了空间几何和笛卡尔空间坐标系，坐标系的具体样子如下图：

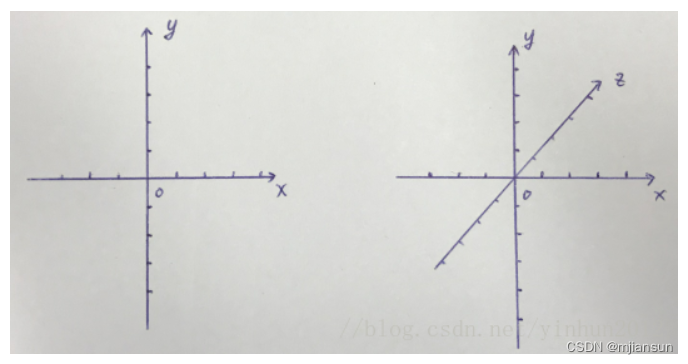
        在这种坐标系中，向量和点的数学描叙会让人迷惑，比如向量AB = (3,5,4)，向量CD =  (3,5,4)，坐标点P =  (3,5,4)，如果在现实世界中，我们肯定不会认为一个质点P和一条线段AB是一个东西，而且也不能认为桌子上一条线段AB和天花板上一条平行且长度相同的线段CD是一个东西。

2.2 透视

        既然谈到现实世界了，我们好好想一下我们感受到的现实世界是怎么样子的？我们通过双眼观察这个世界，太阳光线照射到物体上，反射进入我们眼睛，光线被晶状体折射后打到视网膜上，呈现了物体倒立的等比缩放图像，经过大脑主动修正，我们就看到正立的物体的图像。我们用眼睛观察世界有一个特点，就是越远的物体看起来就越小，而且我们还能通过“越远越小”这种视觉效果估算距离。假如我们站在现实世界中的一条很远的马路上，马路尽头在我们眼中就交汇成了一个点，如下图：

        这种现象被称为透视现象，同样的存在这种现象的空间被称为透视空间。

       透视现象在现实生活中无处不在，计算机视觉中也遵循这个原理。

       在笛卡尔空间中，两条平行线是永远不会相交的，但是在透视空间中，两条平行线会相交于一点，这是两种空间最大的区别。

        想像一下一条长直的铁杆长度等于上图街道的宽度，同时平行于地面，并且处于越来越远的运行状态，假设刚开始铁杆的向量AB为(x=10,y=1,z=1,w=1)，那么随着铁杆越来越远，x,y,z,w的数值越来越小并且x/w,y/w,z/w的数值保持不变，这样的话（x,y,z,w）既能表示同样的向量长度方向，又能区分向量的位置，所以w分量的引入确实起到了实际作用。

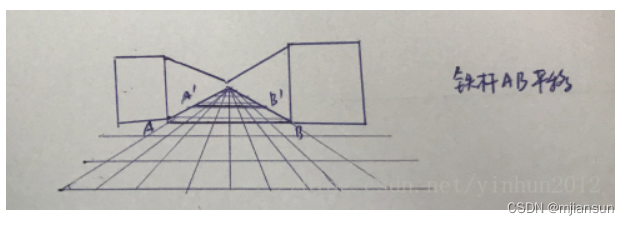
        如上图，假如铁杆移动到无限远处，那么铁杆向量AB在笛卡尔空间下表示为(∞,∞,∞) ，那么在透视空间的齐次坐标表示下AB = (10/w = ∞,1/w = ∞,1/w = ∞,w=0)，这么一来就说明w = 0就表示了透视空间中一个向量平移成一个点。

2.3 仿射

        同时我看过一篇文章，谈到计算机图形学中的图形变换，实际上是在仿射空间中进行的，而并在一般的向量空间中。

        仿射空间是向量空间的一个子集，或者说仿射空间是向量空间的一种，但是区别于向量空间的特殊之处就是仿射空间没有选定原点，一般的向量空间我们都会人为的定义一个“绝对中心”也就是原点，仿射空间则不局限于这个“绝对中心”。

        仿射空间的坐标原点是不确定的，一个仿射空间A变换成另一个仿射空间B就是A经过线性变换(旋转)然后平移，变成B。那么我们可以认为向量空间中图形的变换，就是从图形的中心心所在的同样中心仿射空间A经过仿射变换变成另一个仿射空间B，这个应该很好理解，因为我们观察unity引擎中表示物体Obj的transform是不是有个worldposition属性，我们可以理解为worldposition属性就代表着当前物体Obj所处的仿射空间A的原点就是worldposition，物体Obj通过变换后transform上的worldposition属性就变成了新的仿射空间B的原点。

这个过程中仿射空间A可能经过了旋转缩放最后再平移变成了仿射空间B，其中的图形也跟着变换，可以理解仿射变换的函数表示：

         γ = T*α+β，其中α为原始图形，T为线性变换矩阵，β为平移向量

        因为β平移无法满足线性f(a+b) = f(a) + f(b)同时f(ka) = k*f(a)的可加性和比例性，所以这个变换暂时不能称为线性变换，但是缩放k倍和旋转θ角这两种变换却是可以的，所以我们需要扩充维度进行β平移的计算，以便达到完美统一的线性变换的目的，如下图（下图中图像表示了旋转和平移，但是公式只表示了平移）：

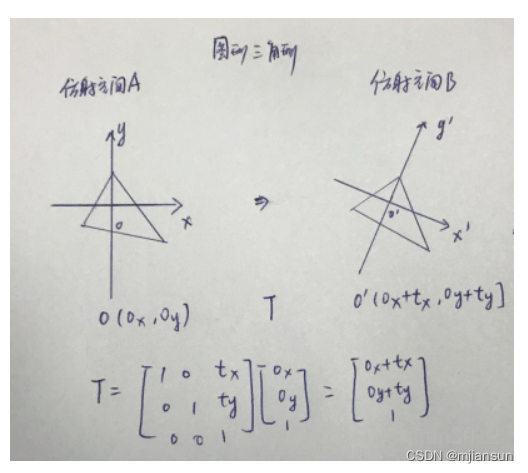
        因为仿射空间的存在，我们认为图形变换就是变换了以图形为原点的仿射坐标，那么我们使用齐次坐标表示法，同时变换矩阵也扩充一个维度称它为”平移维度“，这时候我们可以利用数学技巧“忽略掉”除了“平移维度”之外的维度，只进行“平移维度”的计算， 根据矩阵乘法的计算规则，那么tx，ty就很自然的处理了两个仿射空间的平移，如下图，忽略黑框中的线性变换方块：

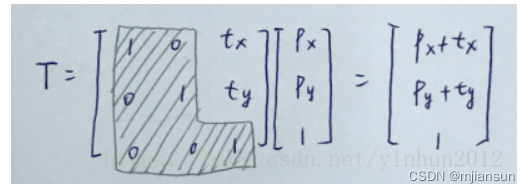
       这大概就是图形学书上面对齐次坐标的作用的解释。

参考

相机标定（一） —— 深入理解齐次坐标及其作用_齐次坐标的作用_人狮子的博客-CSDN博客

(356条消息) 线性代数：理解齐次坐标_羊羊2035的博客-CSDN博客

https://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html