理解深度学习的卷积操作
左侧图像模拟一个图像数据,当我们用右侧的卷积核对其进行卷积操作时,设置stride = 1或不设置默认为1,每次对应的格子相乘完之后,卷积核向右移动一格,再次对应相乘得到结果,如下过程简单演示。卷积核就像一个小窗口,在图像上滑动,每次观察 3x3 大小的区域。为了方便对比演示,将卷积核更改了一下颜色。如下图,卷积核从左上角开始进行第一次卷积操作。卷积核向右移动一个像素,进行第二次卷积操作。
目录
理解卷积操作
什么是卷积?
卷积(Convolution)是一种数学运算,用于描述两个函数(或信号、图像)之间相互作用的关系。在离散情况下,卷积的数学表达式为:
其中,是输入数据(如图像、信号),
是卷积核(或滤波器),
是输出位置索引。
为什么要用卷积?
-
高效处理高维数据
图像、视频等高维数据的直接全连接处理计算量巨大。卷积通过局部连接和参数共享降低计算复杂度。 -
层次化特征学习
深层卷积神经网络(CNN)通过堆叠卷积层,逐步提取从低级(边缘)到高级(物体部件、整体)的特征。 -
保留空间结构
卷积操作保持输入数据的空间或时序关系,适合处理具有局部相关性的数据(如图像像素、时间序列)。
特征提取
卷积通过滑动窗口(卷积核)对输入数据进行局部加权求和,能够捕捉局部特征
在神经网络中,卷积与信号工程学数学表达式类似但并不相同,神经网络中卷积操作是做点积运算。
卷积核的感受野概念
感受野(Receptive Field)指卷积神经网络(CNN)中某一层特征图上的像素点(图像经过卷积得到的特征图上每个像素是一个神经元)在原始输入图像上映射的区域大小。注意这里只是指原始图像,感受野反映了特征图中每个单元能够“看到”的输入范围,是理解CNN层次化特征提取的关键概念。
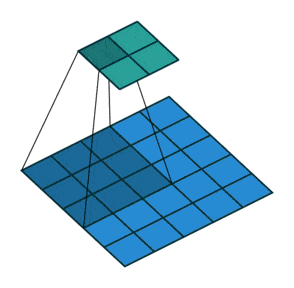
经过多层卷积后,神经元的感受野的大小会越来越大,通常,感受野越大,模型效果会更好。
比如VGG网络进入全连接前,每个神经元感受野大小为212。
对于像素级别的预测任务(也叫密集预测任务),如需要给原始图像中每个像素点进行分类的
语义分割任务,语音处理领域的立体声和光流估计任务等,FC层之前的感受野的大小至关重
要,(一个神经元要知道足够大范围的信息才能了解自己在全局中的位置和作用 )对于其他任务,我们也会尽量保证分类前感受野的大小是足够大的。
加了池化层后,感受野的扩大速率更快。
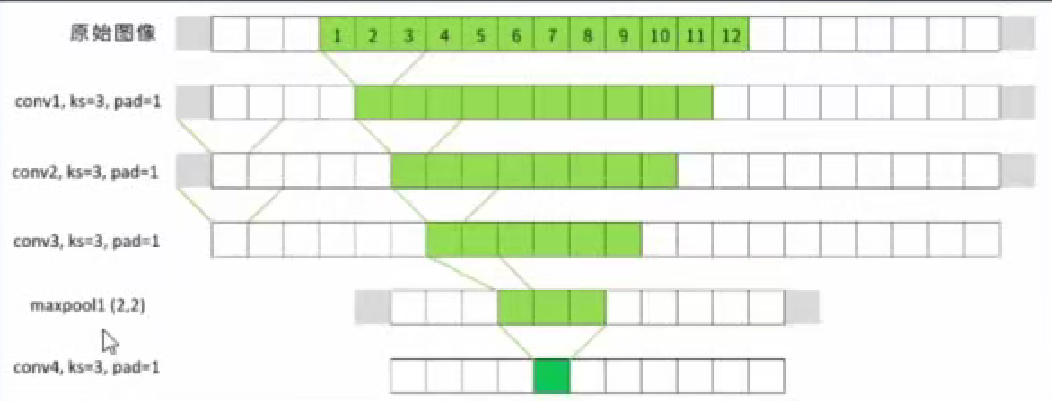
感受野的大小没有上限!随着深度加深,感受野会变成下图第三个图,周围有很多黑边。

为什么要让感受野变成这样,观察整张图像不就好了吗,实际上,这和人眼类似,“中间清晰,周围模糊”,虽然我们能看到一片区域。但能够看清的只有我们眼球盯的位置,也就是余光的位置我们眼睛能够感受到,但却看不清。
卷积神经网络的感受野也是一样。对于特征图来说,每个神经元所捕捉到的感受野区域不同,
但这些区域是会有重叠的,并且很好理解的是,越是位于中间的像素,被扫描的次数越多,感
受野重叠也就会越多。
2次扫描中的区域,padding = 0, kernel = 3x3, stride = 1。
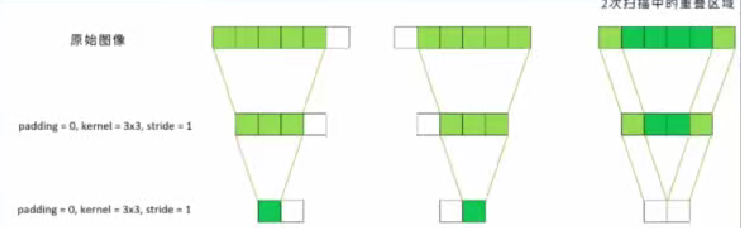
对整个特征图来说,重叠越多的部分,信息就越饱满,“看得就越清晰”,而重叠较少的部分,信
息就比较稀疏,因此就会“模糊!因此,位于图像中间的像素有更多可以影响最终特征图的“路
径”,他们对最终特征圈的影响更大,对卷积网络的分类造成的影响也会更大,论文
《Understand the Effective Receptive Field in Deep CNN》中严格证明了原始图像上的像素
点对最终特征图的影响力呈现二元高斯分布,只有极少数位于非常中心的像素点能够对最终的特征图产生巨大影响。
二维卷积计算
在深度学习中,对一张图片,经过一系列的卷积池化全连接操作进行特征提取,变成一个机器能够理解的向量。
左侧图像模拟一个单通道的图像数据(6×6),当我们用右侧的卷积核对其进行卷积操作时,设置步长stride = 1或不设置默认为1,每次对应的格子相乘完之后,卷积核向右移动一格,再次对应相乘得到结果,如下过程简单演示。
卷积核就像一个小窗口,在图像上滑动,每次观察 3x3 大小的区域。在神经网络中,卷积核的参数就是w,神经网络的权重参数!
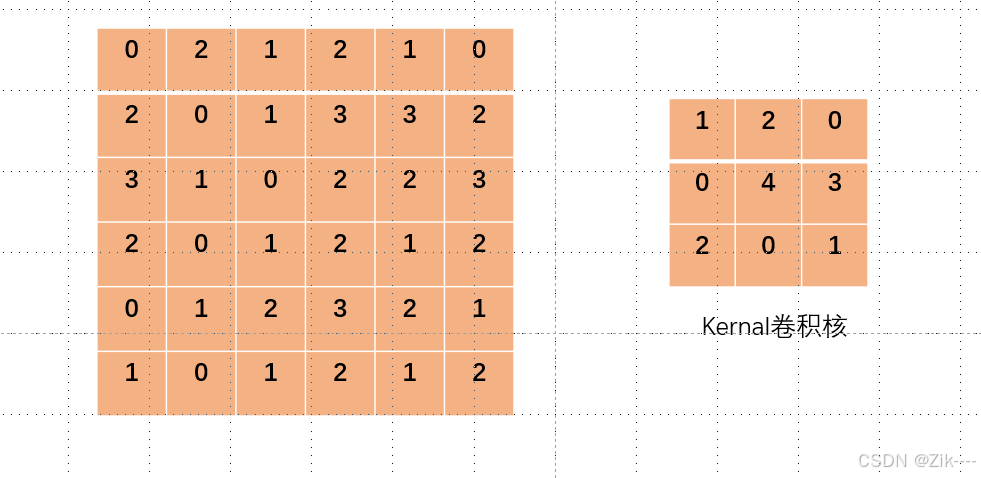
为了方便对比演示,将卷积核更改了一下颜色。
如下图,卷积核从左上角开始进行第一次卷积操作。
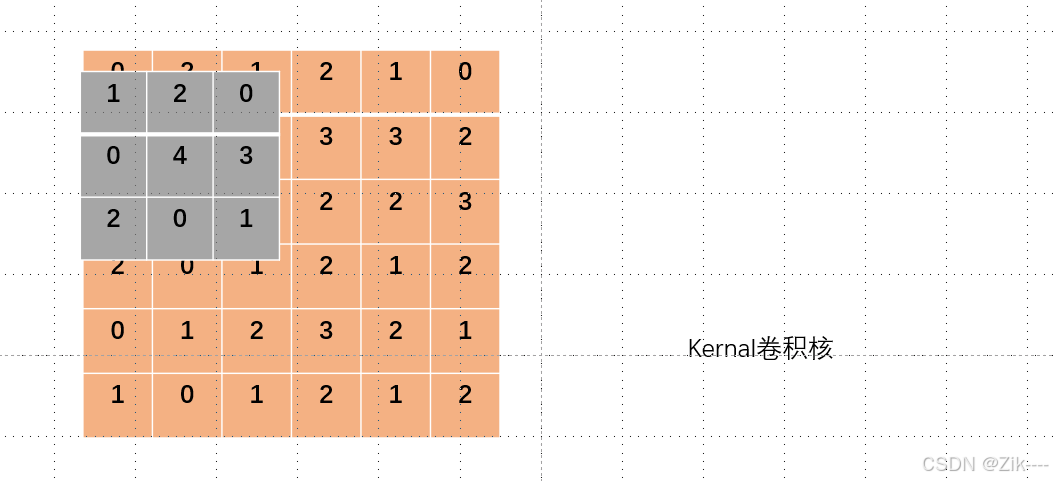
卷积核向右移动一个位置,进行第二次卷积操作。
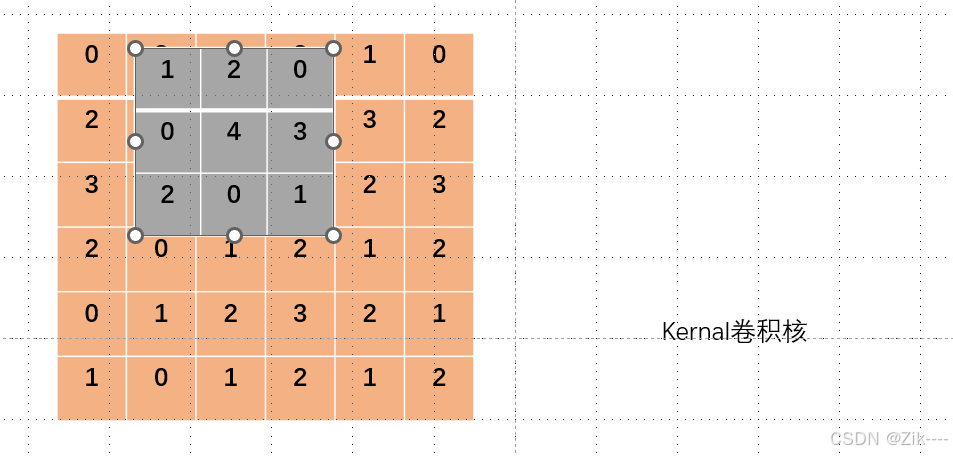
填充方式:
当卷积核在图像上滑动到右边(或其他边界位置)没有数据时,如下图,通常有以下几种处理方式:
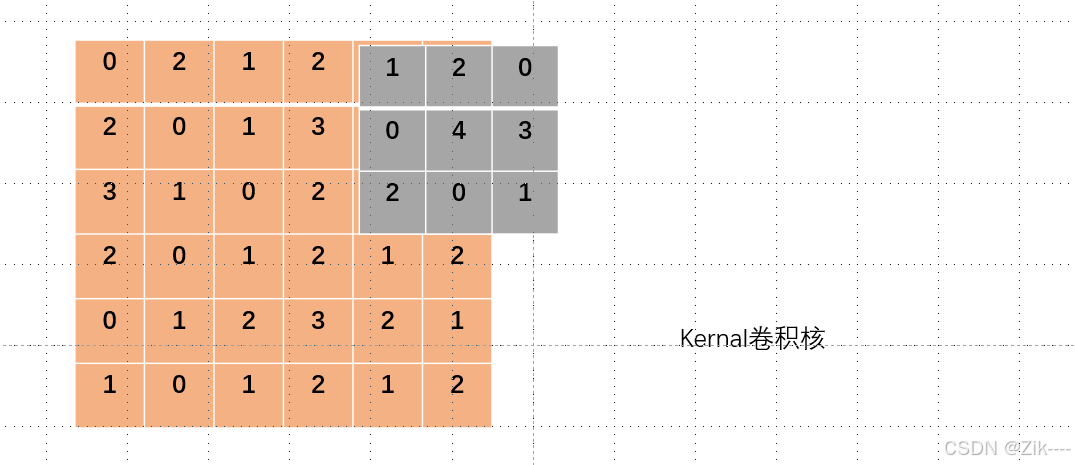
1. 零填充(Zero - Padding)
在原始图像的边界周围填充一定数量的 0。这样,当卷积核滑动到边界时,卷积核覆盖的区域仍然有数据(0乘任何数为0,这样不会影响结果)在 PyTorch 中使用 nn.Conv2d 时,padding 参数可以设置填充的大小,如 padding = 1 就表示在图像四周各填充 1 行 1列,如下图。
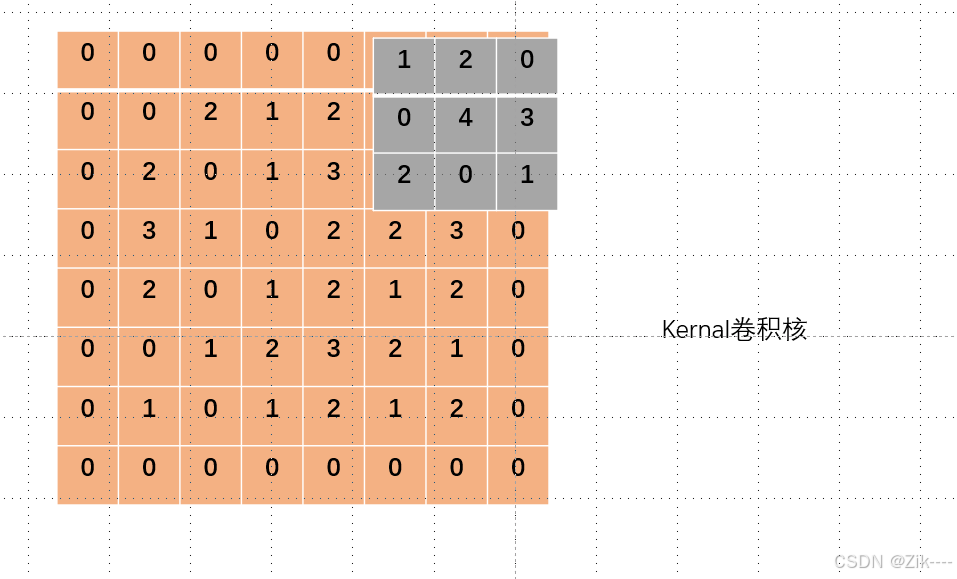
2. 复制填充(Replication Padding)
不是填充 0,而是复制边界上的像素值来填充。例如,如果图像最右边的像素值是 5,那么在右边填充时,填充的像素值都为 5。这种方式可以在一定程度上保留边界的特征信息,避免因填充 0 而可能引入的噪声或特征突变。在一些深度学习框架中,有专门的函数或参数设置来实现复制填充。
3. 不填充(No Padding)
当卷积核滑动到边界没有数据时,就停止滑动。这种情况下,输出特征图的尺寸会比输入图像小。计算公式为如下(其实就是最基础最重要的那个公式少了2padding)其中 Win 和 Hin 是输入图像的宽和高, K是卷积核的大小,S 是步长。这种方式会丢失边界部分的信息,可能对一些需要完整边界信息的任务产生影响。
第一个图是最基础的哪个公式。
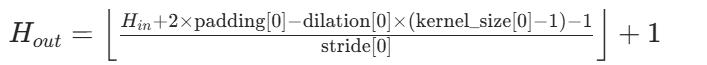

若 p=0 ,dilation=1,上述公式可简化为下面的公式:
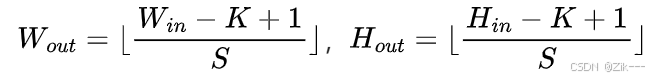
下面,模拟一下这个过程。
代码演示:
import torch
import torch.nn.functional as F
# 定义输入张量 input,它是一个 4x4 的二维矩阵
# 这个矩阵模拟了待卷积处理的图像数据
input = torch.tensor([
[0, 1, 2, 3],
[2, 1, 3, 2],
[0, 1, 3, 0],
[0, 4, 1, 2],
])
# 定义卷积核张量 kernel,它是一个 3x3 的二维矩阵
# 卷积核用于在输入数据上进行卷积操作,提取特征
kernel = torch.tensor([
[2, 1, 0],
[2, 1, 0],
[1, 0, 2],
])
# 此时的input和kernalshape不符合要求
print(input.shape)
# 为了能将输入数据用于 PyTorch 的二维卷积函数 F.conv2d,需要调整其形状
# F.conv2d 函数要求输入数据的形状为 (batch_size, in_channels, height, width)
# 这里将 input 调整为形状为 (1, 1, 4, 4) 的四维张量,其中 batch_size=1 表示一批只有一个样本,in_channels=1 表示输入通道数为 1
# 即需要在前面增加两个维度。
input = torch.reshape(input, (1, 1, 4, 4))
# 同样,卷积核也需要调整形状以符合 F.conv2d 函数的要求
# 要求卷积核的形状为 (out_channels, in_channels, kernel_height, kernel_width)
# 这里将 kernel 调整为形状为 (1, 1, 3, 3) 的四维张量,out_channels=1 表示输出通道数为 1,如果是图像,则是一个灰度图。
kernel = torch.reshape(kernel, (1, 1, 3, 3))
# 使用 F.conv2d 函数进行二维卷积操作,stride=1 表示卷积核每次移动的步长为 1 个像素
# 卷积操作会在输入数据上滑动卷积核,计算对应位置的乘积和,得到卷积结果
output1 = F.conv2d(input, kernel, stride=1)
# 改变stride,即卷积核每次移动 2 个像素
# 步长的改变会影响卷积结果的大小
output2 = F.conv2d(input, kernel, stride=2)
# 设置padding = 1,对原图形二维矩阵上下左右各填充数字一列,一行数字
output3 = F.conv2d(input,kernel,stride=1,padding=1)
# 打印三种不同情况的结果
print(output1)
print(output2)
print(output3)
输出结果:
可自己算一算,看看结果是否一致。
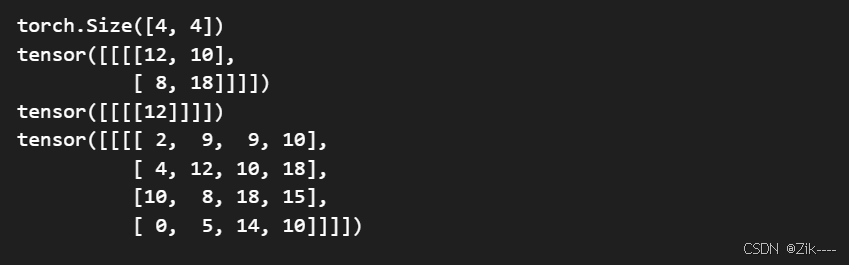
下面进行实际的创建自己的神经网络,并对图像数据进行卷积操作。
Dilated Convotion(膨胀卷积 空洞卷积)
膨胀卷积是一种特殊的卷积操作,通过引入膨胀率(dilation rate)在卷积核中插入间隔(空洞)来扩大感受野,同时不增加参数量或计算复杂度。
原始感受野大小为3。

普通卷积的膨胀率 r=1 ,设置r=2,膨胀率为2后,即卷积核的相邻权重之间会插入 1 个 “空洞”,感受野大小扩大为5×5。
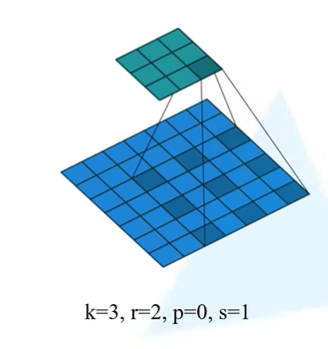
我们这里以0来表示这些空洞,实际上这些0是不存在的,不参与点积运算。
例如,膨胀率为2时,2×2卷积核的实际覆盖区域为3×3(但仅计算4个非零权重)。
原始的卷积核:
[2, 1],
[2, 1]设置 r=2 后,卷积核变为:
[2, 0, 1]
[0, 0, 0]
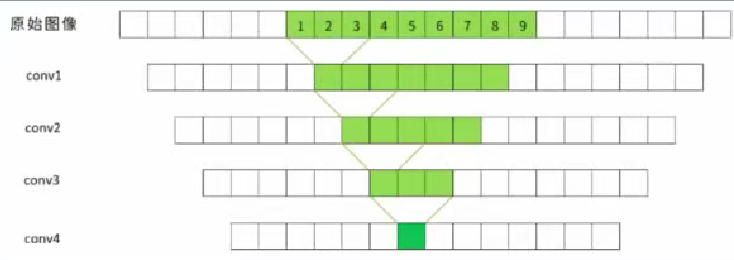
[2, 0, 1]你是否产生这样的疑问:虽然看上去感受野的面积是被放大了,但是跳过其中的像素点不进行计算,真的算是放大了本应该用来捕获信息的感受野吗?这样的放大是有效的吗?从直觉来看,这样做应该会产生非常多的信息损失,要了解膨胀卷积真正的力量,还需要将多个卷积层连起来考虑。
对于没有膨胀的原始卷积,在第三层卷积层的特征图上,任意两个相邻的神经元的感受野如下所示。其中绿色是绿色神经元的感受野,黄色是黄色神经元的感受野,橙色是两个神经元在各层上感受野的交叉部分。不难看出,对于普通卷积,相邻神经元的感受野大概率是里复的,两个神经元的感受野合起来尺寸有8x8的大小,而其中7x7的部分都是重复的。
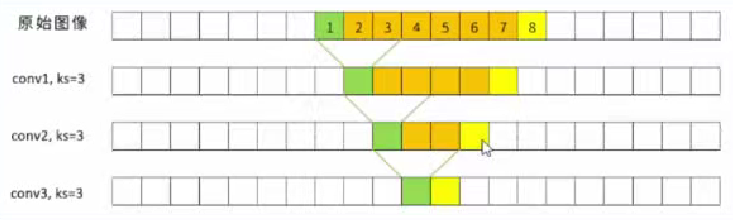
但如果加入膨胀卷积呢?
假设从第一个卷积层开始,我们就采用dilation=2的设置,在第三个卷积层生成的特征图上,相
邻的两个神经元所涉及到的计算点如图所示:每次进行计算时,都是上一层不相邻的9个像素被
扫描到。虽然在生成单个神经元时,上一层的特征图上留下了不少末计算的空隙,但相邻的神
经元却很好地补上了这些没有被计算的部分,使得相邻两个神经元之间没有重复进行扫描。此
时,两个相邻神经元的感受野合起来就有14x14的大小,比起没有膨胀卷积时的感受野面积大了
约3倍左右。
这个性质可以被很好地利用,当我们将膨胀率调大,并且让膨胀卷识层与普通卷积
层串联使用时,单个像素的感受野可以被持续放大(这种情况下,两个像素共同的感受野自然
更大了)。如下图所示:
另外为什么不直接增大卷积核的尺寸呢?而要做这种填0操作,前面提到,在神经网络中 ,卷积核中的数字就是参数权重,如果直接增大卷积核的尺寸,无疑会使我们的参数激增。这些卷积核中填充为0的位置会损失对应数据的信息,但能使我们在不增加参数的情况下,扩大感受野。
Transposed Convolution(转置卷积):
作用:上采样,膨胀卷积是对卷积核进行填充,而转置卷积是对原始图像进行填充。
转置卷积的运算步骤:
在输入特征图元素间填充s-1行、列0,
在输入特征图四周填充k-p-1行、列0,
将卷积核参数上下、左右翻转,
做正常卷积运算(p=0,s=1)
比如下图元素间填充s-1=0行,四周填充k-p-1=2行。
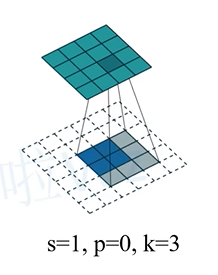
再比如下图元素间填充s-1=1行,四周填充k-p-1=1行。
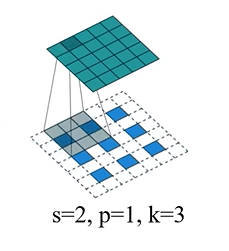
原始输入图像经过填充后的图像大小计算如下:

对于 s=2,p=1,k=3,填充后的图像H和W为(3-1)× 2 - 2×1 + 3 = 5。
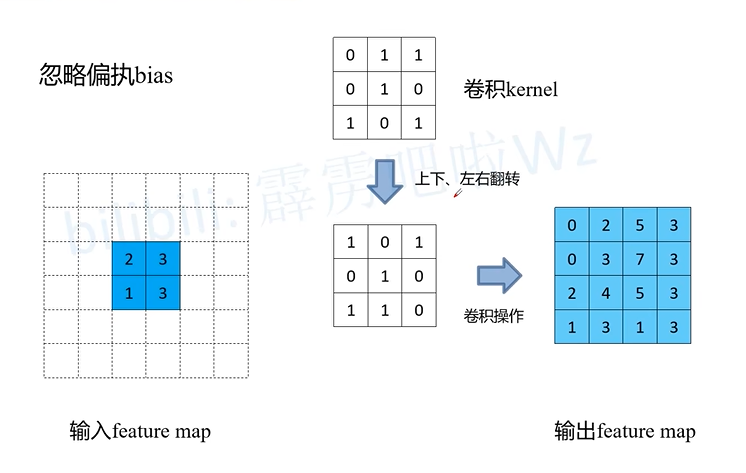
二维卷积的实战演示:
代码演示:
import torch
import torchvision
# 从 torchvision 的转换模块中导入 ToTensor 类,用于将图像数据转换为张量
from torchvision.transforms import ToTensor
# 从 torch 的神经网络模块中导入必要的类
from torch.nn import Module, Conv2d
# 从 torch 的数据加载器模块中导入 DataLoader 类,用于批量加载数据
from torch.utils.data import DataLoader
# 从 torch 的可视化工具模块中导入 SummaryWriter 类,用于将训练过程中的数据写入 TensorBoard
from torch.utils.tensorboard import SummaryWriter
# 卷积操作
# 加载 CIFAR-10 数据集
# root 参数指定数据集的存储路径,这里设置为 './dataset',表示在当前目录下的 dataset 文件夹中存储数据集
# train=False 表示加载测试集,CIFAR-10 数据集分为训练集和测试集,这里选择测试集
# transform=ToTensor() 表示将图像数据转换为张量,方便后续的神经网络处理
# download=False 表示如果数据集不存在则不进行下载,需要确保数据集已经存在于指定路径
dataset = torchvision.datasets.CIFAR10(root='./dataset', train=False, transform=ToTensor(), download=False)
# 使用 DataLoader 批量加载数据集
# batch_size=64 表示每个批次包含 64 个样本,就像我们把一叠书(数据集)分成一捆一捆的,每捆有 64 本
dataloader = DataLoader(dataset, batch_size=64)
# 定义一个自定义的神经网络模块 zzy,继承自 nn.Module
# nn.Module 是 PyTorch 中所有神经网络模块的基类,就像一个大的工具箱,我们要在这个工具箱的基础上创建自己的小工具
class zzy(Module):
def __init__(self):
# 调用父类的构造函数进行初始化,就像我们在制作小工具之前,先把大工具箱里的基本功能准备好
super(zzy, self).__init__()
# 定义一个二维卷积层
# in_channels=3 表示输入图像的通道数为 3(RGB 图像),可以想象成一幅彩色画有红、绿、蓝三个颜色通道
# out_channels=6 表示输出特征图的通道数为 6,这意味着我们会用 6 个不同的“放大镜”(卷积核)去观察这幅彩色画,得到 6 种不同的观察结果
# kernel_size=3 表示卷积核的大小为 3x3,卷积核就像一个小窗口,在图像上滑动,每次观察 3x3 大小的区域
# stride=1 表示卷积核的步长为 1,即每次滑动一个像素,就像我们拿着小窗口一格一格地移动
# padding=0 表示不进行填充,填充就像是给图像周围加一圈边框,这里不加边框
self.conv1 = Conv2d(in_channels=3, out_channels=6, kernel_size=3, stride=1, padding=0)
def forward(self, x):
# 前向传播过程,将输入 x 通过卷积层 conv1 进行处理
# 就像我们把彩色画放进小工具里,经过“放大镜”的观察,得到新的图像特征
x = self.conv1(x)
return x
# 创建 zzy 类的一个实例
# 这就像我们根据设计好的小工具图纸,制作出了一个实际可用的小工具
zzy1 = zzy()
# 打印小工具的结构,让我们看看它长什么样
print(zzy1)
# 创建一个 SummaryWriter 对象,指定日志存储路径为 '/logs'
# SummaryWriter 就像一个记录员,会把我们训练过程中的数据记录下来,方便我们后续查看
writer = SummaryWriter('/logs')
# 初始化一个计数器,用于记录当前处理的批次数量
step = 0
# 遍历数据加载器中的每个批次的数据
# 就像我们一捆一捆地处理书,每次处理一捆
for data in dataloader:
# 从批次数据中解包出图像数据和对应的标签
# 可以想象成我们从一捆书中挑出了书(图像)和书的编号(标签)
imgs, targets = data
# 将图像数据输入到我们创建的神经网络模块中进行处理,得到输出
# 就像把书放进小工具里进行加工,得到新的结果
output = zzy1(imgs)
# 打印输入图像的形状,让我们了解输入数据的格式
print(imgs.shape)
# 打印输出特征图的形状,让我们了解经过卷积处理后的数据格式
print(output.shape)
# 使用 SummaryWriter 将输入图像写入 TensorBoard,方便我们可视化输入数据
# 就像记录员把原始的书拍了张照片,存起来供我们查看
writer.add_images('input', imgs, step)
# 尝试将输出特征图的形状调整为 (-1, 3, 30, 30),但这里有个问题,torch.reshape 不会改变原张量,需要赋值给原变量
# 这里的调整是为了让输出特征图能够以图像的形式可视化,就像我们把加工后的结果重新整理成可以展示的样子
output = torch.reshape(output, (-1, 3, 30, 30))
# 使用 SummaryWriter 将调整形状后的输出特征图写入 TensorBoard,方便我们可视化处理后的结果
# 就像记录员把加工后的书也拍了张照片,存起来供我们查看
writer.add_images('output', output, step)
# 批次计数器加 1,表示处理完了一个批次
step += 1
# 关闭 SummaryWriter,就像记录员完成了工作,把本子合上
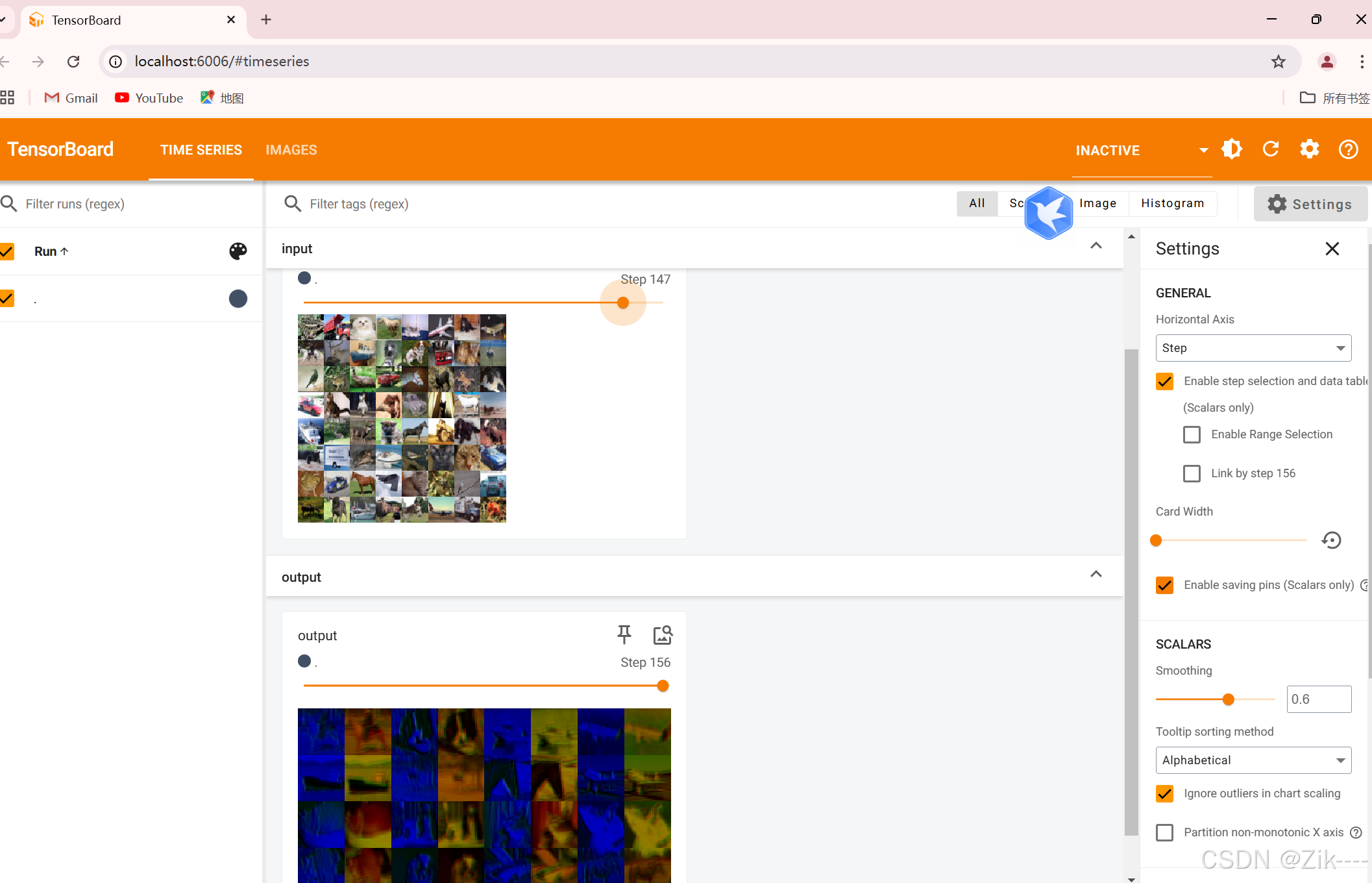
writer.close() 此时在终端输入指令 tensorboard --logdir=/logs,启动 TensorBoard 服务后,会在终端输出一个 URL,通常是 http://localhost:6006 。打开你的浏览器,访问该 URL,即可看到 TensorBoard 的界面,如下。
上方是原图像,下方是经过卷积操作后的图像。
三维卷积
在深度学习中,通常数据是三维的,为什么使用卷积处理数据而不是全连接呢,在三维数据里,卷积能够大大提升数据处理的效率
时间序列
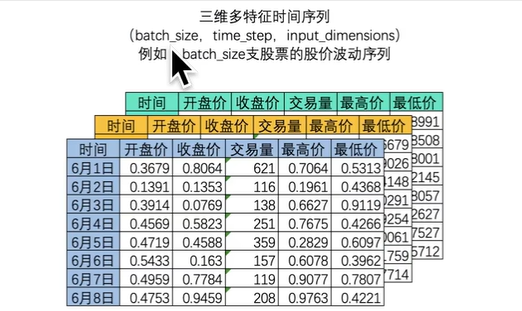
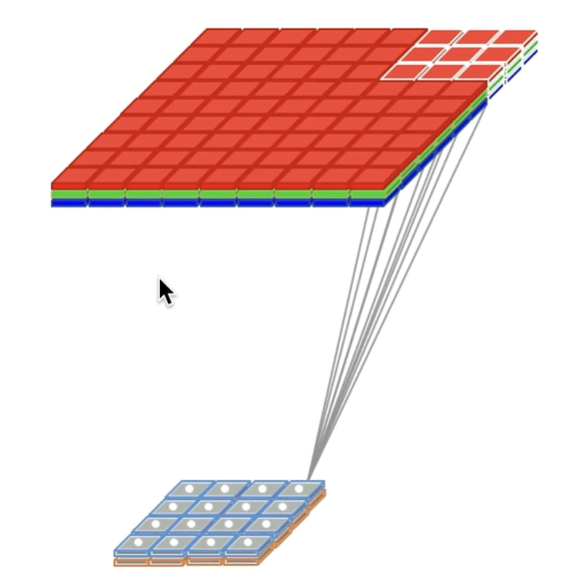
卷积不止能够在特征上并行,还能够同时对多张时间序列表单进行处理,假设现在有红、绿、蓝三张时间序列表单,则我们可以一次性扫描掉所有表单的数据 。
补充:
在 PyTorch 中使用 circular 填充进行卷积操作时,输出尺寸不可能大于输入尺寸。
不变性:
在计算机视觉、尤其是图像识别相关的任务中,不变性(invariance,或lnvariant)是至关重要、甚至影响建模和数据处理流程的一种性质。不变性是指,如果我们能够识别出一张图像中的一个对象,那即便这个对象以完全不同的姿态呈现在别的图像中,我们依然可以识别出这个对象,对算法而言,不变性意味着“在训练集上被成功识别的对象,即便以不同的姿态出现在测试集也能被识别。
比如对于下面这只猫:

模型难以识别同样的这只猫出现的不同姿态,即模型还没理解这张图像的内容:

反而是下面这种像素排列具有很高的相似度会被模型判断为同一只猫。

不变性包含平移不变性,旋转不变性,尺寸不变性,明度不变性等等,如下图:

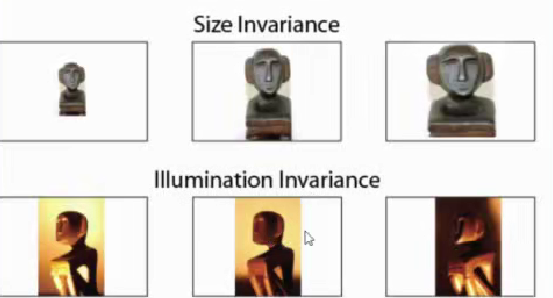
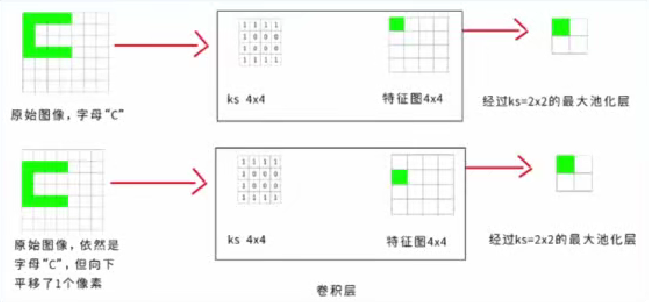
为了卷积神经网络具备各种不变性,需要做数据增强

平移不变性在大多数情况下很好,但当在做密集型任务时,比如人脸识别,模型会认为左图和右图都是一张人脸。

其他不变性也有同样的问题。
卷积层的参数数量:

通常,卷积核的大小是比较小的,那么主要影响卷积层的参数数量的就是输入输出通道输数。
卷积核的尺寸:
为什么我们通常选择小的卷积核,比如3×3,而不一次性选择一个大的卷积核完成几层小卷积核同样的操作呢?

这是参数量的原因,两层3×3的卷积核,卷积核s上的为为s上的为为上的参数量
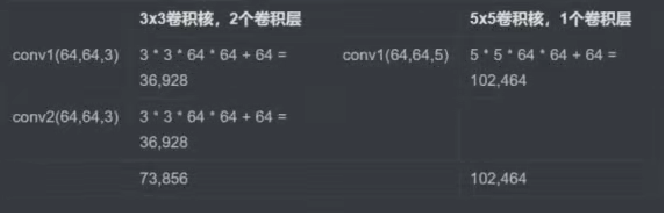
最小的卷积核尺寸为1×1,此时叫逐点卷积。
在使用3×3卷积的两侧使用1×1卷积,能答复降低参数量,即首先用1×1的卷积核在不改变特征图大小的情况下,降低特征图的通道数,再做3×3卷积,再把通道数升回来。这样在两个1×1卷积核中间加入其他卷积核的架构叫“瓶颈设计”。

更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容










所有评论(0)