最大信息熵模型

根据最大信息熵原理，信息熵最大时得到的模型是最优模型，即最大信息熵模型。

最大信息熵原理

信息论的开创者香农将信息的不确定程度称为熵，为了与热力学中熵的概念区分，这种信息的不确定程度又称信息熵。

最大信息熵原理认为在所有可能的概率模型中，熵最大的那个模型为最优模型。

贝叶斯概率模型

贝叶斯定理

 

贝叶斯定理认为任何变量都可以看作一个随机变量，可以用一个概率分布来描述。 当这个分布在实验前就已经确定，则称这个分布为先验概率分布。

贝叶斯公式的本质是基于先验概率分布和似然函数来求解后验概率分布。

不同先验概率分布对后验影响很大。

朴素贝叶斯

朴素贝叶斯的原理推导

朴素贝叶斯是基于贝叶斯定理和特征条件独立性假设的分类算法。具体而言，对于给定训练数据，朴素贝叶斯首先基于特征条件独立性假设学习输入和输出的联合概率分布，然后对于新的实例，利用贝叶斯定理计算出最大的后验概率。朴素贝叶斯不会直接学习输入和输出的联合概率分布，而是通过学习类的先验概率和类条件概率来完成。

步骤： 

numpy代码实现

import numpy as np
import pandas as pd

### 构造数据集
x1 = [1,1,1,1,1,2,2,2,2,2,3,3,3,3,3]
x2 = ['S','M','M','S','S','S','M','M','L','L','L','M','M','L','L']
y = [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1]
df = pd.DataFrame({'x1':x1, 'x2':x2, 'y':y})
print(df.head())
X = df[['x1', 'x2']]
y = df[['y']]

### 定义朴素贝叶斯模型训练过程
def nb_fit(X, y):
    '''
    输入：
    X：训练样本输入，pandas数据框格式
    y：训练样本标签，pandas数据框格式
    输出：
    classes：标签类别
    class_prior：类先验概率分布
    class_condition：类条件概率分布
    '''
    # 标签类别
    classes = y[y.columns[0]].unique()
    # 标签类别统计
    class_count = y[y.columns[0]].value_counts()
    # 极大似然估计：类先验概率
    class_prior = class_count/len(y)
    # 类条件概率：字典初始化
    prior_condition_prob = dict()
    # 遍历计算类条件概率
    # 遍历特征
    for col in X.columns:
        # 遍历类别
        for j in classes:
            # 统计当前类别下特征的不同取值
            p_x_y = X[(y==j).values][col].value_counts()
            # 遍历计算类条件概率
            for i in p_x_y.index:
                prior_condition_prob[(col, i, j)] = p_x_y[i]/class_count[j]
    return classes, class_prior, prior_condition_prob

classes, class_prior, prior = nb_fit(X, y)
print(classes, class_prior, prior)

def predict(X_test):
    res = []
    for c in classes:
        p_y = class_prior[c]
        p_x_y = 1
        for i in X_test.items():
            p_x_y *= prior[tuple(list(i)+[c])]
        res.append(p_y*p_x_y)
    return classes[np.argmax(res)]

X_test = {'x1': 2, 'x2': 'S'}

print('测试数据预测类别为：', predict(X_test))

sklearn代码实现

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
"""
高斯朴素贝叶斯。
根据似然函数的不同还有其他算法  
'BernoulliNB', 'GaussianNB', 'MultinomialNB', 'ComplementNB','CategoricalNB'
"""
gnb = GaussianNB()
y_pred = gnb.fit(X_train, y_train).predict(X_test)
print("Accuracy of GaussianNB in iris data test:",
      accuracy_score(y_test, y_pred))

贝叶斯网络

朴素贝叶斯的假设是特征之间是独立。但是在实际情况下，独立过于严格。

贝叶斯网络去除了条件独立性假设。

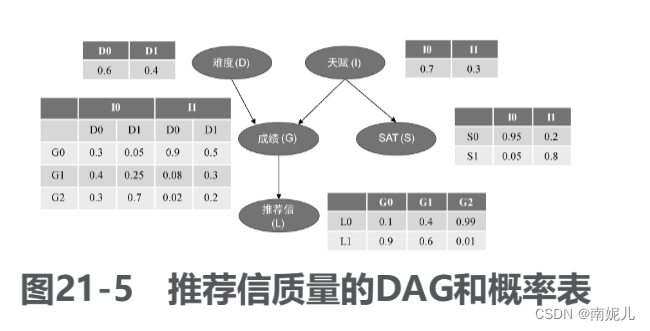
有向无环图（directed acyclic graph，DAG），每个结点表示一个特征或者随机变量，特征之间的关系则用箭头连线来表示。贝叶斯网络中每个结点还有一个与之对应的概率表。

# 导入pgmpy相关模块
from pgmpy.factors.discrete import TabularCPD
from pgmpy.models import BayesianModel
#构建模型，指定各变量之间的关系
letter_model = BayesianModel([('D', 'G'),
                               ('I', 'G'),
                               ('G', 'L'),
                               ('I', 'S')])

# 传入各个节点的条件概率分布，
grade_cpd = TabularCPD(
    variable='G', # 节点名称
    variable_card=3, # 节点取值个数
    values=[[0.3, 0.05, 0.9, 0.5], # 该节点的概率表
    [0.4, 0.25, 0.08, 0.3],
    [0.3, 0.7, 0.02, 0.2]],
    evidence=['I', 'D'], # 该节点的依赖节点
    evidence_card=[2, 2] # 依赖节点的取值个数
)
# 考试难度的条件概率分布
difficulty_cpd = TabularCPD(
            variable='D',
            variable_card=2,
            values=[[0.6], [0.4]]
)
# 个人天赋的条件概率分布
intel_cpd = TabularCPD(
            variable='I',
            variable_card=2,
            values=[[0.7], [0.3]]
)
# 推荐信质量的条件概率分布
letter_cpd = TabularCPD(
            variable='L',
            variable_card=2,
            values=[[0.1, 0.4, 0.99],
            [0.9, 0.6, 0.01]],
            evidence=['G'],
            evidence_card=[3]
)
# SAT考试分数的条件概率分布
sat_cpd = TabularCPD(
            variable='S',
            variable_card=2,
            values=[[0.95, 0.2],
            [0.05, 0.8]],
            evidence=['I'],
            evidence_card=[2]
)

# 将各节点添加到模型中，构建贝叶斯网络
letter_model.add_cpds(
    grade_cpd,
    difficulty_cpd,
    intel_cpd,
    letter_cpd,
    sat_cpd
)
# 导入pgmpy贝叶斯推断模块
from pgmpy.inference import VariableElimination
# 贝叶斯网络推断
letter_infer = VariableElimination(letter_model)
# 天赋较好且考试不难的情况下推断该学生获得成绩等级
prob_G = letter_infer.query(
            variables=['G'],
            evidence={'I': 1, 'D': 0})
print(prob_G)

EM算法

作为一种迭代算法，EM算法用于包含隐变量的概率模型参数的极大似然估计。EM算法包括两个步骤：E步，求期望（expectation）；M步，求极大（maximization）。

极大似然估计

似然函数

通常情况，概率可以帮助我们推出结果。但是在生活中，我们通常是知道结果，而不知道事件发生的概率。比如说一个箱子中有黑白两种球，这时我们并不知道每个球被抽中的概率。这时我们可以通过随机抽样，假设抽了五次，分别为白，黑，黑，黑，黑。那么我们如果通过结果来估计黑球被抽中的概率呢？首先，我们假设黑球被抽中的概率是P,那么白球被抽中的概率就是1-P。那么可以知道得到这次结果的概率为（1-P）*P*P*P*P。这就是似然函数。似然函数以关于模型参数的函数，表示模型参数的可能性。而结果发生了，说明这个事件的可能性是最大的。所以这种估计参数的方法也叫做极大似然估计。

极大似然估计

极大似然估计是一种参数估计方法，可以通过若干次实验来估计参数的值。

举个例子：

如果要了解学校学生的身高分布。首先假设身高这个随机变量服从正太分布，但是对于正太分布参数的均值和方差是不知道的。全校和很多学生，所以一个个测其实挺麻烦的。这时，可以通过统计抽样的方法，选取一组样本，假设随机抽取100个。现在我们用这100个样本的值，来估计全校学术身高的分布。

 EM算法的原理推导

EM算法也叫做最大期望算法。

EM算法是一种迭代优化策略，由于它的计算方法中每一次迭代都分两步，其中一个为期望步（E步），另一个为极大步（M步），所以算法被称为EM算法（Expectation-Maximization Algorithm）。

# 导入numpy库
import numpy as np

### EM算法过程函数定义
def em(data, thetas, max_iter=30, eps=1e-3):
    '''
    输入：
    data：观测数据
    thetas：初始化的估计参数值
    max_iter：最大迭代次数
    eps：收敛阈值
    输出：
    thetas：估计参数
    '''
    # 初始化似然函数值
    ll_old = -np.infty
    for i in range(max_iter):
        ### E步：求隐变量分布
        # 对数似然
        log_like = np.array([np.sum(data * np.log(theta), axis=1) for theta in thetas])
        # 似然
        like = np.exp(log_like)
        # 求隐变量分布
        ws = like/like.sum(0)
        # 概率加权
        vs = np.array([w[:, None] * data for w in ws])
        ### M步：更新参数值
        thetas = np.array([v.sum(0)/v.sum() for v in vs])
        # 更新似然函数
        ll_new = np.sum([w*l for w, l in zip(ws, log_like)])
        print("Iteration: %d" % (i+1))
        print("theta_B = %.2f, theta_C = %.2f, ll = %.2f"
              % (thetas[0,0], thetas[1,0], ll_new))
        # 满足迭代条件即退出迭代
        if np.abs(ll_new - ll_old) < eps:
            break
        ll_old = ll_new
    return thetas

# 观测数据，5次独立试验，每次试验10次抛掷的正反次数
# 比如第一次试验为5次正面5次反面
observed_data = np.array([(5,5), (9,1), (8,2), (4,6), (7,3)])
# 初始化参数值，即硬币B的正面概率为0.6，硬币C的正面概率为0.5
thetas = np.array([[0.6, 0.4], [0.5, 0.5]])
thetas = em(observed_data, thetas, max_iter=30, eps=1e-3)

隐马尔可夫模型

隐马尔可夫模型（hidden Markov model, HMM）是由隐藏的马尔可夫链随机生成观测序列的过程，是一种经典的概率图模型。

概率图模型

概率图模型是一种基于概率理论、使用图论方法来表示概率分布的模型。图是由结点以及连接结点的边组成的集合。

根据概率图的边是否有向，可分为有向概率图模型和无向概率图模型

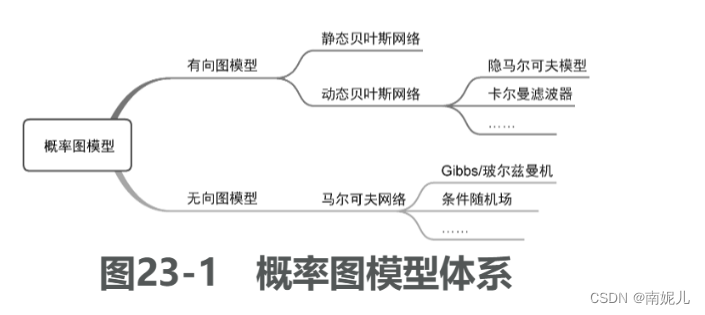
HMM的定义和相关概念

马尔可夫模型

马尔可夫模型描述了一类重要的随机过程：对于一个随机变量序列，序列中各随机变量并不是相互独立的，每个随机变量的值可能会依赖于之前的序列状态。

 

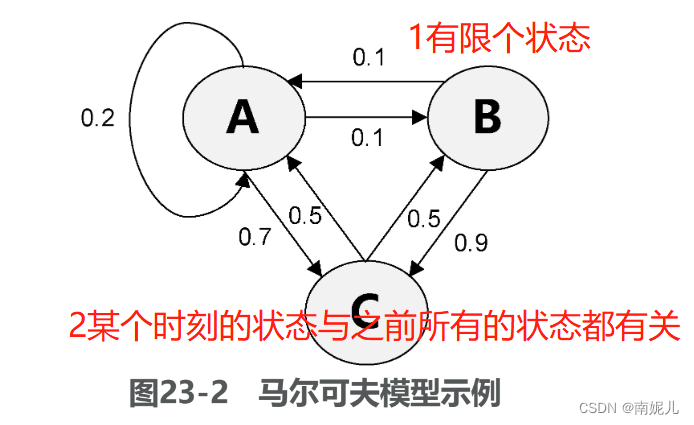
 HMM

 HMM是关于时序的概率模型，描述一个隐藏的马尔可夫链随机生成不可观测的随机状态序列，再由各个状态生成一个观测而产生随机序列的过程。其中隐藏的马尔可夫链随机生成的状态的序列称为状态序列，每个状态产生的观测构成的序列称为观测序列。

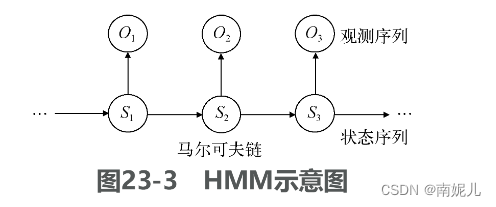
举个例子：

 

 

# 导入numpy库
import numpy as np
### 定义HMM类
class HMM:
    def __init__(self, N, M, pi=None, A=None, B=None):
        # 可能的状态数
        self.N = N
        # 可能的观测数
        self.M = M
        # 初始状态概率向量
        self.pi = pi
        # 状态转移概率矩阵
        self.A = A
        # 观测概率矩阵
        self.B = B
    # 根据给定的概率分布随机返回数据
    def rdistribution(self, dist):
        r = np.random.rand()
        for ix, p in enumerate(dist):
            if r < p:
                return ix
            r -= p
    # 生成HMM观测序列
    def generate(self, T):
        # 根据初始概率分布生成第一个状态
        i = self.rdistribution(self.pi)
        # 生成第一个观测数据
        o = self.rdistribution(self.B[i])
        observed_data = [o]
        # 遍历生成后续的状态和观测数据
        for _ in range(T-1):
            i = self.rdistribution(self.A[i])
            o = self.rdistribution(self.B[i])
            observed_data.append(o)
        return observed_data
# 初始状态概率分布
pi = np.array([0.25, 0.25, 0.25, 0.25])
# 状态转移概率矩阵
A = np.array([
    [0,  1,  0, 0],
    [0.4, 0, 0.6, 0],
    [0, 0.4, 0, 0.6],
    [0, 0, 0.5, 0.5]])
# 观测概率矩阵
B = np.array([
    [0.5, 0.5],
    [0.6, 0.4],
    [0.2, 0.8],
    [0.3, 0.7]])
# 可能的状态数和观测数
N = 4
M = 2
# 创建HMM实例
hmm = HMM(N, M, pi, A, B)
# 生成观测序列
print(hmm.generate(5))

HMM的三个经典问题

确定了HMM之后，就有三个经典问题需要我们解决，分别是概率计算问题、参数估计问题和序列标注问题。

两个重要假设，这两个假设在三个问题的推导中起着重要作用。

 

概率计算

给定观测序列，计算生成该观测序列的概率

### 前向算法计算条件概率
def prob_calc(O):
    '''
    输入：
    O：观测序列
    输出：
    alpha.sum()：条件概率
    '''
    # 初始值
    alpha = pi * B[:, O[0]]
    # 递推
    for o in O[1:]:
        alpha_next = np.empty(4)
        for j in range(4):
            alpha_next[j] = np.sum(A[:,j] * alpha * B[j,o])
        alpha = alpha_next
    return alpha.sum()
# 给定观测
O = [1,0,1,0,0]
# 计算生成该观测的概率
print(prob_calc(O))

小结

 

条件随机场

条件随机场是一类最适合预测任务的判别模型，其中相邻的上下文信息或状态会影响当前预测。

概率无向图

概率图是一种由图表示的概率分布模型。

 

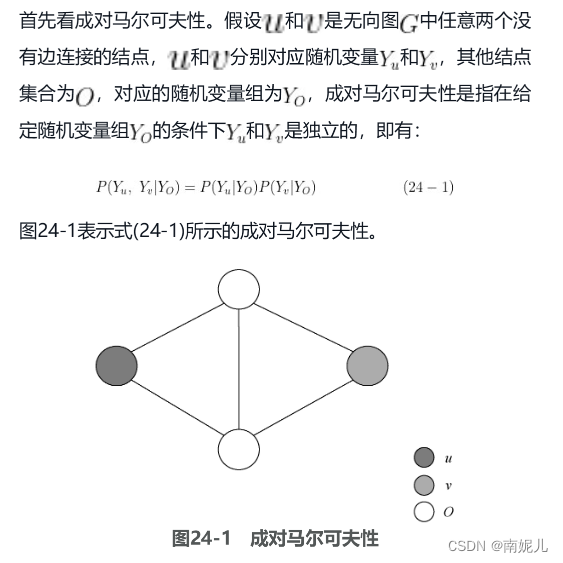
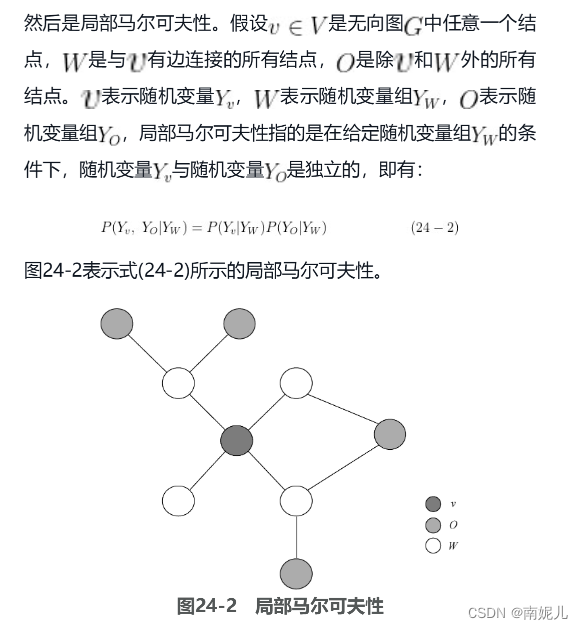
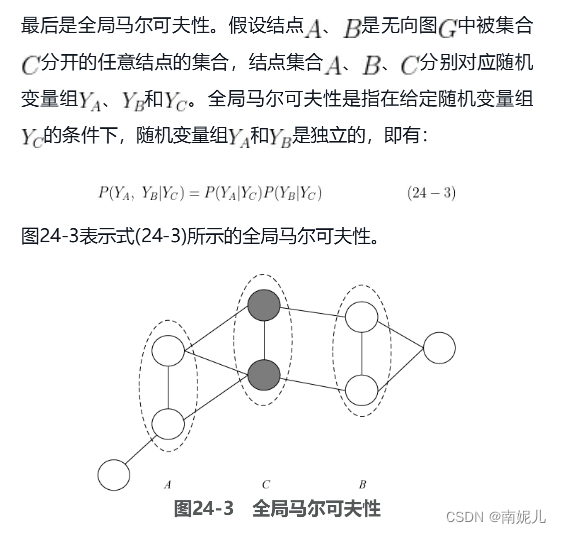
 如果联合概率分布[插图]能够满足成对马尔可夫性、局部马尔可夫性和全局马尔可夫性，那么它就可以称为概率无向图模型，也称马尔可夫随机场

马尔可夫链蒙特卡洛方法

马尔可夫链蒙特卡洛方法是一种将马尔可夫链和蒙特卡洛方法相结合、用于在概率空间中进行随机采样来估算目标参数的后验概率分布方法。

相关概念

马尔可夫链

马尔可夫链的定义比较简单。对于一个随机变量序列，假设某一时刻状态的取值只依赖于它的前一个状态，符合该特征的随机变量序列就可以称作马尔可夫链。

蒙特卡洛算法

蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，它是一种思想或者方法的统称，而不是严格意义上的算法。蒙特卡罗方法的起源是1777年由法国数学家布丰（Comte de Buffon）提出的用投针实验方法求圆周率，在20世纪40年代中期，由于计算机的发明结合概率统计理论的指导，从而正式总结为一种数值计算方法，其主要是用随机数来估算计算问题。

计算圆周率

M = input('请输入一个较大的整数')  # 输入的数一般要很大才能保证所求结果不会与圆周率产生较大误差
N = 0  # 累计落在园内的随机点的个数，初始值为零

import math
import random
from matplotlib import pyplot as plt

for i in range(int(M)):
    # x = random.random()  # 利用random（）产生随机数或者是伪随机数
    # y = random.random()
    x=random.uniform(-1,1)
    y=random.uniform(-1,1)
    if math.sqrt(x ** 2 + y ** 2) < 1:  # 判断产生的随机点是否落在单位圆内
        N = N + 1  # 对落在圆内的点进行累加
        plt.plot(x,y,'ro')
    else:
        plt.plot(x,y,'b*')

plt.show()

pi = 4 * N / int(M)

print(pi)
print('误差',abs(math.pi-pi)/math.pi)

计算定积分

n=int(input('请输入一个较大的整数'))   #要确保输入的整数足够大
 
m=0                                  
 
import random
 
for i in range(n):
    x = random.random()              
    y = random.random()
    if x**2>y:                       #表示该点位于曲线y=x^2的下面
        m=m+1
 
R=m/n
 
print(R)

MCMC

MCMC方法是用来在概率空间，通过随机采样估算兴趣参数的后验分布。

总结

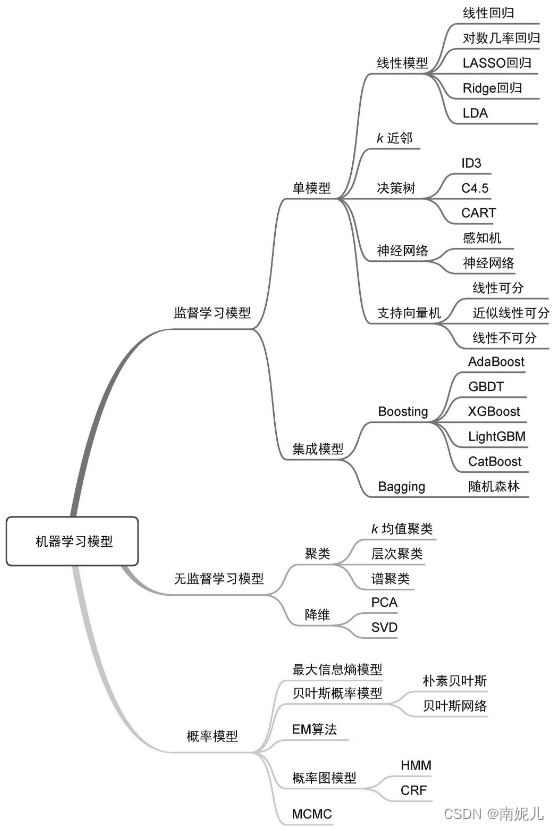
 单模型与集成模型

从模型的个数和性质角度来看，可以将机器学习模型划分为单模型（single model）和集成模型（ensemble model）。

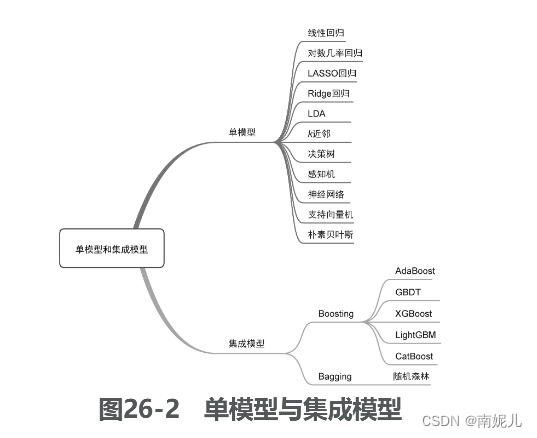
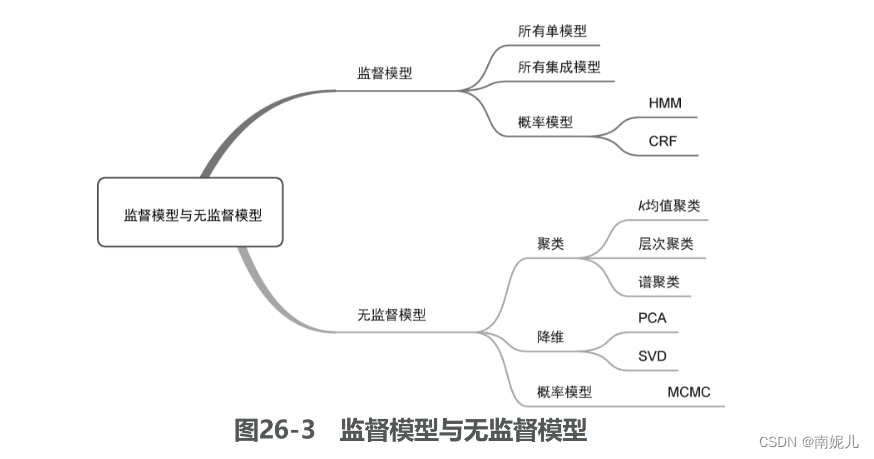
监督模型与无监督模型

 监督模型（supervised model）和无监督模型（unsupervised model）代表了机器学习模型最典型的划分方式，几乎所有模型都可以归类到这两类模型当中。监督模型是指模型在训练过程中根据数据输入和输出进行学习，监督模型包括分类（classification）、回归（regression）和标注（tagging）等模型。无监督模型是指从无标注的数据中学习得到模型，主要包括聚类（clustering）、降维（dimensionality reduction）和一些概率估计模型。

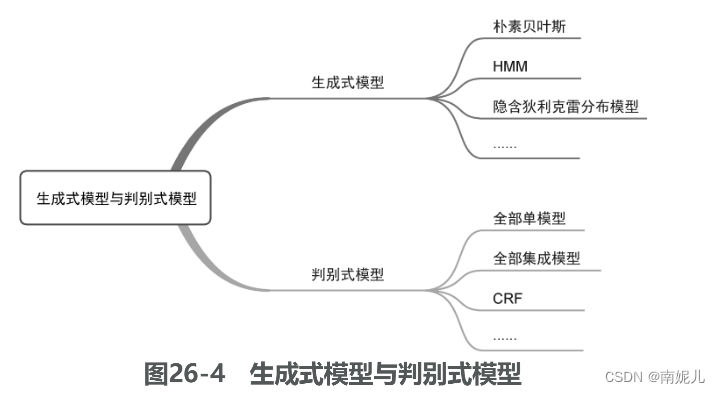
生成式模型与判别式模型

 

 

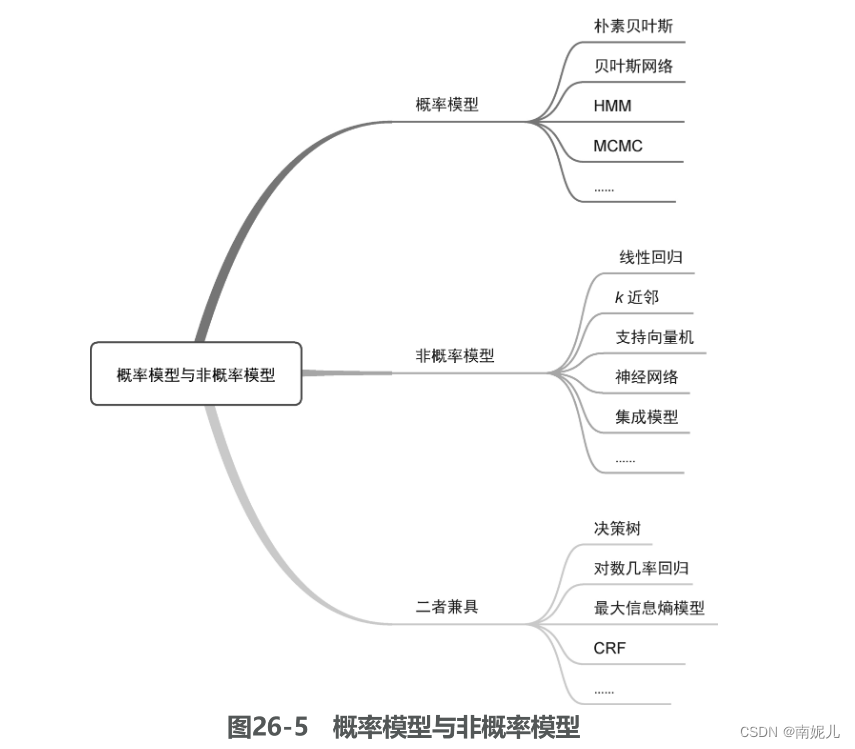
 概率模型与非概率模型

 

 

# 人工智能 # 算法
Logo
EazyDevelop社区

一站式 AI 云服务平台

更多推荐

cover

5分钟搞定！MySQL/PostgreSQL 到 Elasticsearch 的实时同步

avatar EazyDevelop社区
cover

两小时，我搭了一套销售提成计算系统

avatar EazyDevelop社区
cover

零代码时代：如何利用聚合API平台快速构建你的专属AI Agent

avatar EazyDevelop社区