机器学习-Logistic回归(Python)
logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同,都具有 w‘x+b,其中w和b是待求参数,其区别在于他们的因变量不同,多重线性回归直接将w‘x+b作为因变量,即y =w‘x+b,而logistic回归则通过函数L将w‘x+b对应一个隐状态p,p =L(w‘x+b),然后根据p 与1-p的大小
Logistic回归
概念
logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同,都具有 w‘x+b,其中w和b是待求参数,其区别在于他们的因变量不同,多重线性回归直接将w‘x+b作为因变量,即y =w‘x+b,而logistic回归则通过函数L将w‘x+b对应一个隐状态p,p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数,就是logistic回归,如果L是多项式函数就是多项式回归。
logistic回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释,多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。
Logistic回归又叫逻辑回归,本质上其实是sigmod激活函数,即:,其中,
,
,m就是特征向量的特征数,我们展开向量积
有:
,为了方便用列向量整齐的表示,我们引入
。设
,则我们有:
,画出y关于z的函数图像有:
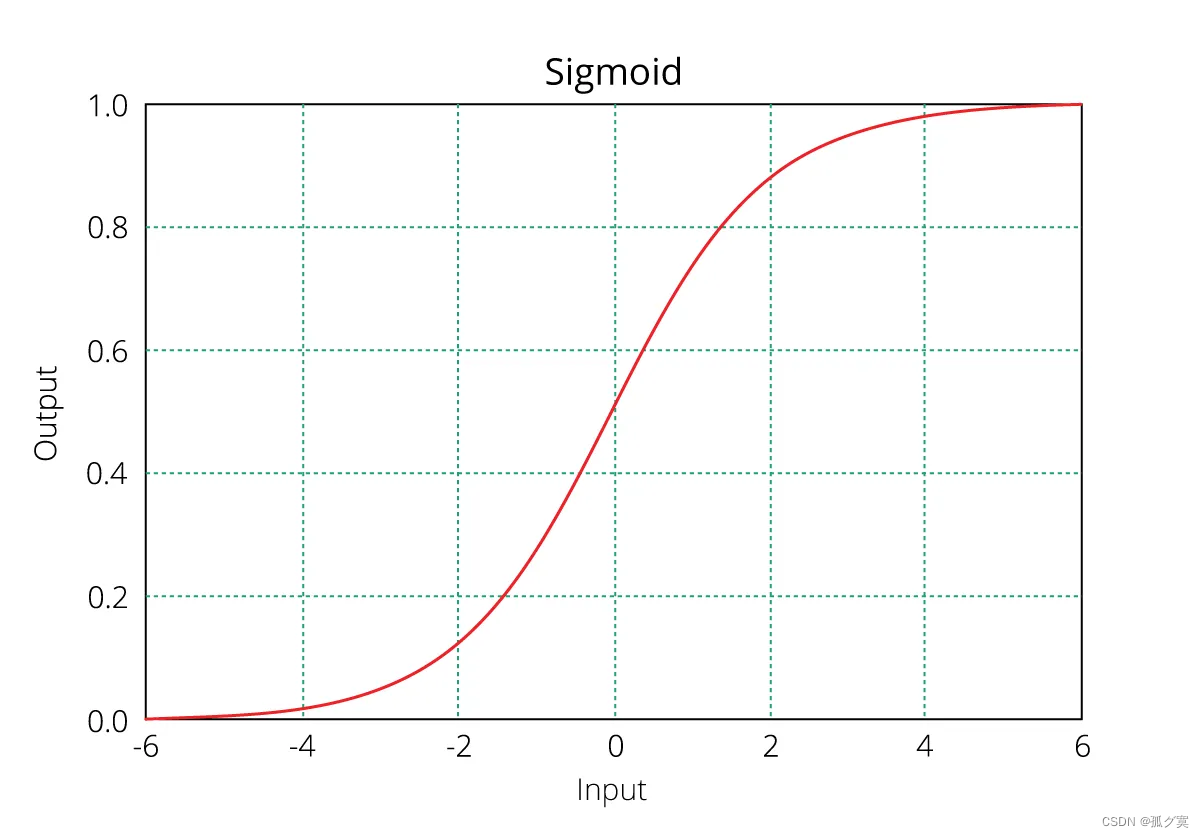
从函数与图像我们可以发现,sigmod曲线的特点是:
当时,
;当
时,
.y的取值范围为[0,1],由此我们可以简单的认为,y的值就是分类结果的概率。
Logistic实验(性别二分类)
导入库
import numpy as np
import matplotlib.pyplot as pltLogistic回归梯度上升优化算法:
def loadDataSet():
dataMat = []
labelMat = []
fr = open('D:/learn/three first/machine learning/Data.txt',encoding='utf-8-sig')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # x1,x2
labelMat.append(int(lineArr[2])) # 类别标签
return dataMat, labelMat
def sigmoid(inX):
return 1.0/(1+np.exp(-inX))
def gradAscent(dataMatIn, classLabels):
'''
通过梯度上升算法找到最佳回归系数,拟合出Logistic回归模型的最佳参数
:param dataMatIn: 二维numpy数组,每列分别代表每个不同的特征,每行则代表每个训练样本
:param classLabels:
:return:
'''
# 转换成numpy矩阵数据类型
dataMatrix = np.mat(dataMatIn)
labelMat = np.mat(classLabels).transpose() # 为了便于矩阵运算,将行向量转换成列向量
m, n = np.shape(dataMatrix)
alpha = 0.001 # 目标移动的步长
maxCycles = 500 # 迭代次数
weights = np.ones((n, 1)) # 构造全一矩阵(n行1列)
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) # 列向量,元素个数等于样本个数
error = (labelMat - h) # 计算差值
weights = weights + alpha * dataMatrix.transpose() * error # 按照差值的方向调整回归系数
return weights
将weight矩阵转换成数组
def reduceOrder(weights):
weightArr=np.array(weights)
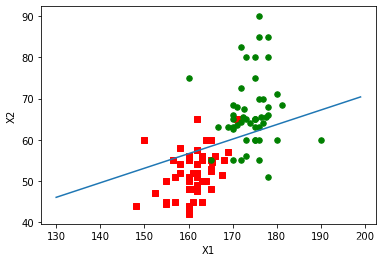
return weightArr分析数据:画出决策边界
def plotBestFit(weights):
'''
画出数据集和Logistic回归最佳拟合直线
:param weights:
:return:
'''
dataMat, labelMat = loadDataSet()
dataArr = np.array(dataMat)
n = np.shape(dataArr)[0]
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1])
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1])
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = np.arange(130, 200, 1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()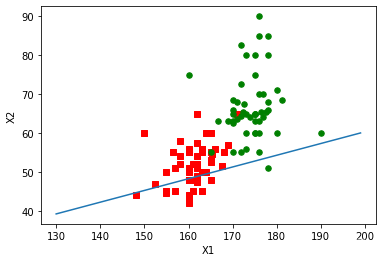
随机梯度上升算法
def stocGradAscent0(dataMatrix, classLabels):
'''
随机梯度上升算法
:param dataMatrix:
:param classLabels:
:return:
'''
m, n = np.shape(dataMatrix)
alpha = 0.01
weights = np.ones(n)
for i in range(m):
# h和error全是数值
h = sigmoid(sum(dataMatrix[i] * weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights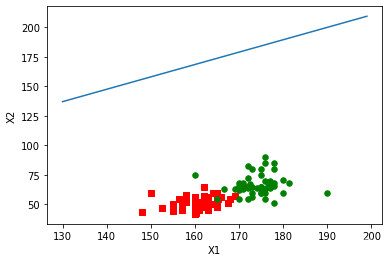
改进的随机梯度上升算法
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
dataMatrix=np.array(dataMatrix)
m,n = np.shape(dataMatrix) #返回dataMatrix的大小 m为行数 n为列数
weights = np.ones(n) #[1. 1. 1.] 初始化参数 类型是array所以注意dataMatrix类型也应该是np.array
for j in range(numIter):
dataIndex = list(range(m)) # [0,1,...99]
for i in range(m):
alpha = 4/(1.0+j+i)+0.01 #降低alpha的大小,每次减小1/(j+i)
randIndex = int(random.uniform(0,len(dataIndex)))#随机选取样本
h = sigmoid(sum(dataMatrix[randIndex]*weights))#选择随机选取的一个样本,计算h。对应位置相乘求和
error = classLabels[randIndex] - h
weights = weights+ alpha* error*dataMatrix[randIndex]#更新回归系数
del(dataIndex[randIndex])#删除已经使用的样本
return weights用logistic回归分类
def classifyVector(inX, weights):
'''
以回归系数和特征向量作为输入计算对应的sigmoid值
:param inX:
:param weights:
:return:
'''
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def colicTest():
fr = open('D:/learn/three first/machine learning/Data.txt',encoding='utf-8-sig')
arrayOLines = fr.readlines()
trainingSet = []
trainingLabels = []
index=0
for line in arrayOLines:
if(index<=80):
currLine = line.strip().split(' ')
lineArr = []
for i in range(2):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[2]))
index+=1
else:break
trainingWeight = stocGradAscent1(np.array(trainingSet), trainingLabels, 500)
errorCount = 0
numTestVec = 0.0
for line in arrayOLines:
if(index>80):
numTestVec += 1.0
currLine = line.strip().split(' ')
lineArr = []
for i in range(2):
lineArr.append(float(currLine[i]))
if int(classifyVector(np.array(lineArr), trainingWeight)) != int(currLine[2]):
errorCount += 1
index+=1
errorRate = (float(errorCount)/numTestVec)
print("the error rate of this test is: %f" % errorRate)
return errorRate
def multiTest():
numTests = 10
errorSum = 0.0
for k in range(numTests):
errorSum += colicTest()
print("after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests)))测试
def main():
'''
dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
plotBestFit(reduceOrder(weights)) # 将weight矩阵转换成数组
'''
'''
dataArr, labelMat = loadDataSet()
weights = stocGradAscent0(np.array(dataArr), labelMat)
plotBestFit(weights)
'''
print(multiTest())
if __name__ == '__main__':
main()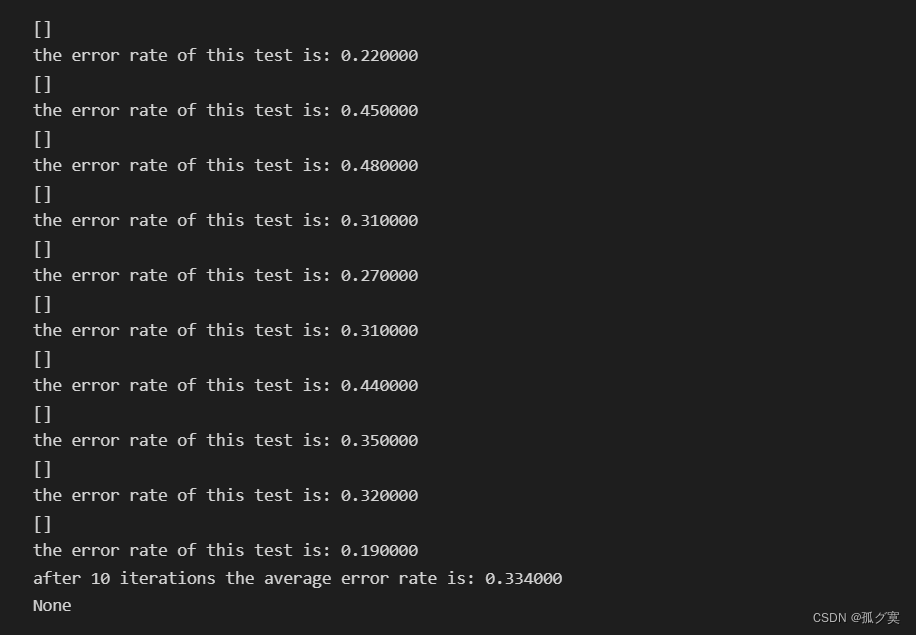
实验结果分析:
从不同梯度算法得出拟合直线对性别的分类可以看出改进的随机梯度算法得出的拟合直线更好,分类的错误率较低,采用改进的梯度算法进行分类,测试得出的平均错误率较低。
总结:
Logistic回归 分类时计算量非常小,速度很快,存储资源低;便利的观测样本概率分数;计算代价不高,易于理解和实现;但当特征空间很大时,逻辑回归的性能不是很好,而且容易欠拟合,一般准确度不太高和不能很好地处理大量多类特征或变量。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容










所有评论(0)