一、ROC曲线介绍

   ROC曲线（Receiver Operating Characteristic curve，受试者工作特征曲线）是评估二分类模型性能的常用工具之一。它通过不同的阈值设置，展示模型在不同分类条件下的表现。ROC曲线以假阳性率（False Positive Rate, FPR）为横轴，真阳性率（True Positive Rate, TPR）为纵轴，能够全面评估模型的分类能力。ROC曲线也叫做相关操作特征曲线。
  ROC分析现在已经在相关的领域得到了很好的发展，特别是在医学，无线电领域中，而且最近在机器学习和数据挖掘领域也得到了很好的发展。

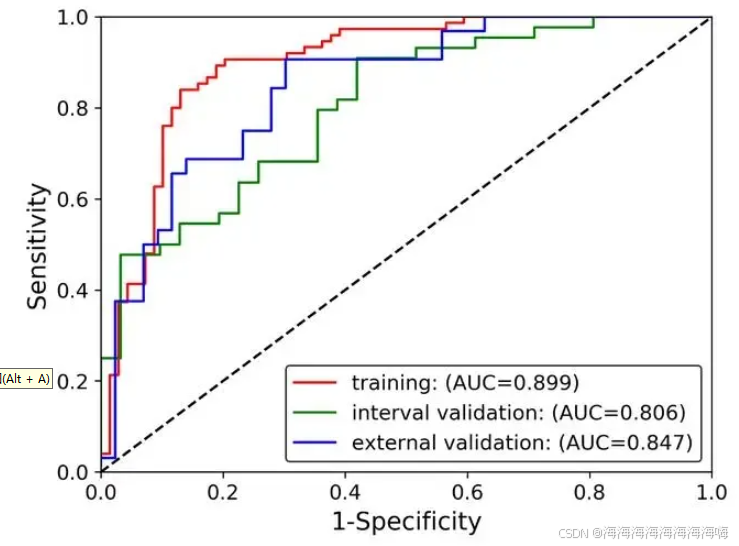
二、ROC曲线的关键指标

1.真阳性率（TPR）：真正分类为阳性的样本占所有真实阳性样本的比例（灵敏度、召回率）。

2.假阳性率（FPR）：被错误分类为阳性的样本占所有真实阴性样本的比例。

3.AUC：ROC曲线下的面积，是衡量分类器优劣的一个数值。AUC的值在0.5到1之间，1表示完美分类器，0.5表示随机分类。

三、ROC曲线的作用

• 可以直观比较不同分类器的性能。

• 不依赖特定的阈值，适合评估在不同阈值下的模型表现。

• AUC值可以帮助快速判断模型的优劣。

四、PR曲线介绍

PR曲线是以召回率（Recall）为横坐标，精确率（Precision）为纵坐标绘制的曲线。这两个指标分别定义如下：

1. 精确率（Precision）：在所有被预测为正例的样本中，真正为正例的比例。计算公式为：Precision = TP / (TP + FP)，其中TP表示真正例的数量，FP表示假正例的数量。
2. 召回率（Recall）：所有实际为正例的样本中被正确预测为正例的比例。计算公式为：Recall = TP / (TP + FN)，其中FN表示假负例的数量。

五、PR曲线的绘制方法

PR曲线的绘制过程涉及以下步骤：

1. 根据模型的预测结果对样本进行排序。
2. 逐一将样本作为正例进行分类，同时计算在不同阈值下的精确率和召回率。
3. 以召回率为横轴，精确率为纵轴，绘制PR曲线。

六、PR曲线的应用场景

1. 不平衡数据集：在不平衡数据集中，即正负样本比例极不平衡的情况下，PR曲线往往比ROC曲线更能反映模型的性能。例如，在信用卡欺诈检测中，欺诈交易往往远少于正常交易，此时PR曲线能够更准确地评估模型在识别少数类（欺诈交易）上的能力。
2. 阈值选择：通过观察PR曲线，可以选择一个合适的阈值，以在精确率和召回率之间取得最佳平衡，满足特定业务场景的需求。

七、PR曲线的评价指标

  平均精度（Average Precision，AP）是PR曲线下的面积，是衡量模型在所有阈值下精确率的平均值。AP值越高，表示模型性能越好。这一指标在评估模型性能时提供了量化的标准。

八、PR曲线在机器应用中的价值

1. 模型评估：PR曲线能够直观地展示模型在不同阈值下的精确率和召回率权衡关系，有助于全面评估模型的性能。
2. 模型优化：通过观察PR曲线，可以发现模型在特定阈值下的表现，从而指导模型优化策略的制定。
3. 业务决策：在业务场景中，可以根据PR曲线选择合适的阈值，以在精确率和召回率之间取得最佳平衡，满足业务需求。

九、PR VS ROC

将两个曲线放在一起进行对比，得到如下结果：

特性	PR曲线	ROC曲线
定义	展示模型在不同阈值下的精确率（Precision）与召回率（Recall）关系	展示模型在不同阈值下的真正率（True Positive Rate, TPR）与假正率（False Positive Rate, FPR）关系
纵轴	精确率（Precision） = TP / (TP + FP)	真正率（TPR） = TP / (TP + FN)
横轴	召回率（Recall） = TP / (TP + FN)	假正率（FPR） = FP / (FP + TN)
适用场景	不平衡数据集，关注正类样本的预测性能	平衡或不平衡数据集，综合评估模型性能
曲线下的面积	AUC-PR（Area Under Precision-Recall Curve）	AUC-ROC（Area Under ROC Curve）
优点	对正类样本的预测性能敏感，适用于不平衡数据集	综合评估模型在不同阈值下的性能，易于解释
缺点	对负类样本的预测性能不敏感	在不平衡数据集中，可能过于乐观地评估模型性能

十、代码实战

好了，现在我们知道了ROC和PR曲线的区别，我们进入实战：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.font_manager import FontProperties

def plot_pr_curve(recall, precision):
    """绘制查准率-查全率（P-R）曲线"""
    fig = plt.figure()
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
    plt.xlabel('查全率(R)', fontproperties=font)
    plt.ylabel('查准率(P)', fontproperties=font)
    x = np.arange(0, 1.1, 0.1)  # 调整刻度以更好地显示曲线
    y = np.arange(0, 1.1, 0.1)
    plt.xticks(x)
    plt.yticks(y)
    plt.plot(recall, precision)
    plt.show()

def plot_roc_curve(fpr, tpr):
    """绘制ROC曲线"""
    fig = plt.figure()
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
    plt.xlabel('假正例率(FPR)', fontproperties=font)
    plt.ylabel('真正例率(TPR)', fontproperties=font)
    x = np.arange(0, 1.1, 0.1)  # 调整刻度以更好地显示曲线
    y = np.arange(0, 1.1, 0.1)
    plt.xticks(x)
    plt.yticks(y)
    plt.plot(fpr, tpr)
    x1 = np.arange(0, 1.0, 0.1)
    plt.plot(x1, x1, color='blue', linewidth=2, linestyle='--')
    plt.show()

def calculate_pr():
    num_real = 0
    # 初始化样本标签，假设1为正例，0为负例
    trainlabel = np.random.randint(0, 2, size=100)

    # 产生100个概率值（置信度），即单个样本值为正例的概率
    traindata = np.random.rand(100)

    # 将样本数据为正例概率从大到小排序返回索引值
    sortedTraindata = traindata.argsort()[::-1]

    k = []
    v = []
    # 统计样本中实际正例的数量
    num = np.sum(trainlabel == 1)
    for i in range(100):
        num_guess = i + 1  # 假设为真的数量
        for j in range(0, i + 1):
            a = sortedTraindata[j]
            if trainlabel[a] == 1:
                num_real += 1  # 假设为真中实际也为真的数量
        p = float(num_real / (num_guess))
        r = float(num_real / (num))
        v.append(p)
        k.append(r)
        num_real = 0
    plot_pr_curve(k, v)

def calculate_roc():
    tp = 0
    # 初始化样本标签，假设1为正例，0为负例
    trainlabel = np.random.randint(0, 2, size=100)

    # 产生100个概率值（置信度），即单个样本值为正例的概率
    traindata = np.random.rand(100)

    # 将样本数据为正例概率从大到小排序返回索引值
    sortedTraindata = traindata.argsort()[::-1]

    k = []
    v = []
    # 统计样本中实际正例的数量
    num = np.sum(trainlabel == 1)
    num1 = 100 - num
    for i in range(100):
        num_guess = i + 1  # 假设为真的数量
        for j in range(0, i + 1):
            a = sortedTraindata[j]
            if trainlabel[a] == 1:
                tp += 1  # 假设为真中实际也为真的数量
        fp = num_guess - tp
        fpr = float(fp / (num1))
        tpr = float(tp / (num))
        v.append(fpr)
        k.append(tpr)
        tp = 0
    plot_roc_curve(v, k)  # 注意：这里k和v的顺序与plot_roc_curve函数的参数顺序相匹配

将PR曲线绘制方法和ROC曲线绘制方法一起丢进PyCharm中，

if __name__ == '__main__':
    # 选择要计算的曲线类型
     calculate_pr()  # 绘制P-R曲线
   # calculate_roc()  # 绘制ROC曲线
    # 你可以取消注释上面的calculate_pr()来绘制P-R曲线

这里有一个问题是当我们绘制PR时要注意注释掉ROC曲线，而当我们绘制ROC曲线时要注释掉PR曲线，本代码在同一时间仅可实现一个图片。

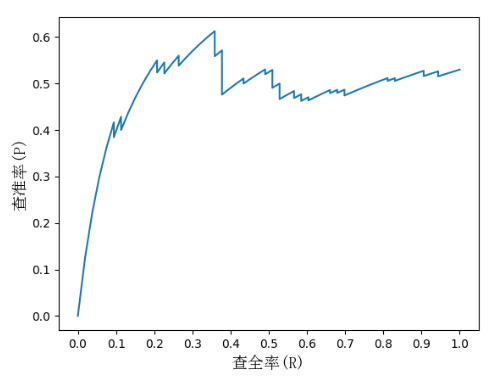
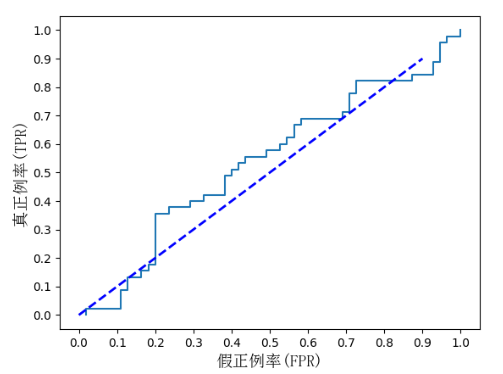
十一、曲线可视化展示

PR曲线：

ROC曲线：