深度学习实验六前馈神经网络（2）——基于前馈神经网络的二分类任务

本次实验基于前馈神经网络对双月数据集进行分类，后附完整的可运行代码本次实验依旧使用双月数据集，使用“sklearn.datasets”的make_moons函数，将噪声设置成0.1（过大就不是双月了），如下图的噪声为0.5：先定义每一层的算子，然后再通过算子组合构建整个前馈神经网络。假设第l层的输入为第l-1层的神经元活性值,经过一个仿射变换，得到该层神经元的净活性值z，再输入到激活函数得到该层神

苏涵.

1137人浏览 · 2024-10-20 17:38:11

苏涵. · 2024-10-20 17:38:11 发布

本次实验基于前馈神经网络对双月数据集进行分类，后附完整的可运行代码

实验步骤如下：

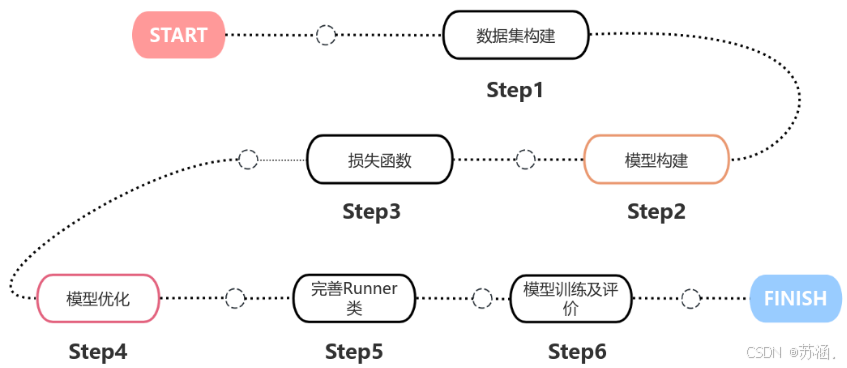
step1数据集构建

本次实验依旧使用双月数据集，使用“sklearn.datasets”的make_moons函数，将噪声设置成0.1（过大就不是双月了），如下图的噪声为0.5：

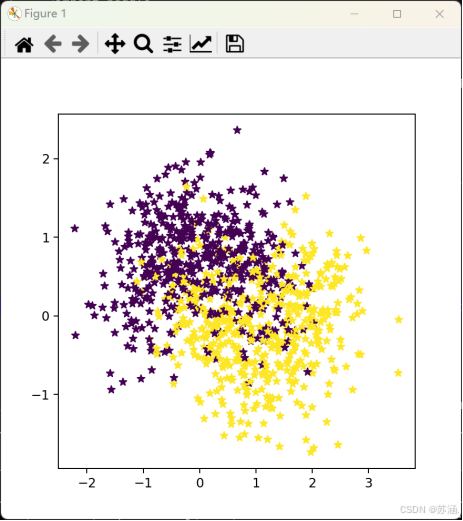
代码如下：

# 构建数据集
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.1)

# 将 y 转换为 Tensor
y = torch.FloatTensor(y).reshape([-1, 1])

# 可视化生成的数据集，不同颜色代表不同类别
plt.figure(figsize=(5, 5))
plt.scatter(x=X[:, 0], y=X[:, 1], marker='*', c=y.numpy())
plt.show()

# 划分数据集, 640条训练集，160条验证集，200条测试集
num_train = 640
num_dev = 160
num_test = 200
X_train, y_train = torch.FloatTensor(X[:num_train]), y[:num_train]
X_dev, y_dev = torch.FloatTensor(X[num_train:num_train + num_dev]), y[num_train:num_train + num_dev]
X_test, y_test = torch.FloatTensor(X[num_train + num_dev:]), y[num_train + num_dev:]

双月数据集如下图：

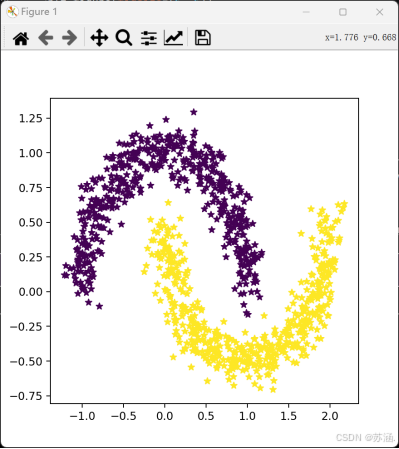
step2模型构建

先定义每一层的算子，然后再通过算子组合构建整个前馈神经网络。假设第l层的输入为第l-1层的神经元活性值 $a^{(l-1)}$ ,经过一个仿射变换，得到该层神经元的净活性值z，再输入到激活函数得到该层神经元的活性值a.

在实践中，为了提高模型的处理效率，通常将N个样本归为一组进行成批地计算。假设网络第l层的输入为 $A^{(l-1)}\in R^{N\times M_{l-1}}$ ,其中每一行为一个样本，则前馈网络中第l层的计算公式为:

$Z^l=A^{l-1}W^l+b^l\in R^{N\times M_{l-1}}, A^{(l)}=F_l(Z^l)\in R^{N\times M_{l}}$

（1）线性层算子（Linear(oP)）

权重参数采用默认的随机初始化，偏置采用默认的零初始化。

代码如下：

# 实现线性层算子
class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=np.random.standard_normal, bias_init=torch.zeros):
        super().__init__()
        self.params = {}
        self.params['W'] = weight_init([input_size, output_size])
        self.params['W'] = torch.as_tensor(self.params['W'], dtype=torch.float32)
        self.params['b'] = bias_init([1, output_size])

        self.inputs = None
        self.grads = {}

        self.name = name

    def forward(self, inputs):
        self.inputs = inputs
        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

    def backward(self, grads):
        self.grads['W'] = torch.matmul(self.inputs.T, grads)
        self.grads['b'] = torch.sum(grads, dim=0)

        # 线性层输入的梯度
        return torch.matmul(grads, self.params['W'].T)

（2）logistic算子

跟之前的差不多，这里不再赘述。

代码如下：

# 实现 Logistic 激活函数
class Logistic(Op):
    def __init__(self):
        super().__init__()
        self.inputs = None
        self.outputs = None
        self.params = None

    def forward(self, inputs):
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

    def backward(self, grads):
        # 计算Logistic激活函数对输入的导数
        outputs_grad_inputs = torch.multiply(self.outputs, (1.0 - self.outputs))
        return torch.multiply(grads, outputs_grad_inputs)

（3）层的串行组合

在定义了神经层的线性层算子和激活函数算子之后，可以不断交叉重复使用它们来构建一个多层的神经网络。实现一个两层的用于二分类任务的前馈神经网络，选用Logistic作为激活函数，可以利用上面实现的线性层和激活函数算子来组装。

代码如下：

# 定义多层感知机模型（MLP）带L2正则化
# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        # 线性层
        super().__init__()
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        # Logistic激活函数层
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

        self.layers = [self.fc1, self.act_fn1, self.fc2, self.act_fn2]

    def __call__(self, X):
        return self.forward(X)

    # 前向计算
    def forward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2

    # 反向计算
    def backward(self, loss_grad_a2):
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)

step3 损失函数

依旧使用二分类交叉熵损失函数。

代码如下：

# 实现交叉熵损失函数
def cross_entropy_loss(y_pred, y_true):
    # 为了避免 log(0)，增加一个小值 eps
    eps = 1e-10
    y_pred = torch.clamp(y_pred, eps, 1.0 - eps)
    # 计算交叉熵损失
    loss = -torch.mean(y_true * torch.log(y_pred) + (1 - y_true) * torch.log(1 - y_pred))
    return loss

step4 模型优化

神经网络的参数主要是通过梯度下降法进行优化的，因此需要计算最终损失对每个参数的梯度。由于神经网络的层数通常比较深，其梯度计算和上一章中的线性分类模型的不同的点在于：线性模型通常比较简单可以直接计算梯度，而神经网络相当于一个复合函数，需要利用链式法则进行反向传播来计算梯度。

代码如下：

# 基础优化器类
class Optimizer(object):
    def __init__(self, model, init_lr=0.1):
        # 保存模型对象
        self.init_lr = init_lr
        self.model = model

    def step(self):
        raise NotImplementedError("Subclasses should implement this method.")


class BatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(BatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        # 参数更新
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
                for key in layer.params.keys():
                    # 假设 layer.grads 存在并已经计算了每一层的梯度
                    layer.params[key] = layer.params[key] - self.init_lr * layer.grads[key]

step5 完善Runner类

与之前不同的是，这个加入了：

（1）支持自定义算子的梯度计算，在训练过程中调用self.loss_fn.backward()从损失函数开始反向计算梯度；

（2）每层的模型保存和加载，将每一层的参数分别进行保存和加载。

代码如下：

# 完善Runner类
class RunnerV2_1(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

        # 记录准确率
        self.train_accuracy = []
        self.dev_accuracy = []

    def accuracy(y_pred, y_true):
        y_pred_labels = (torch.sigmoid(y_pred) >= 0.5).float()  # 根据阈值进行预测
        return (y_pred_labels == y_true).float().mean()

    def train(self, train_set, dev_set, save_dir=None, probabilities=None, **kwargs):
        num_epochs = kwargs.get("num_epochs", 0)
        log_epochs = kwargs.get("log_epochs", 100)

        best_score = 0
        for epoch in range(num_epochs):
            X, y = train_set
            logits = self.model(X)

            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)
            self.train_loss.append(trn_loss.item())

            # 计算训练准确率
            trn_score = self.metric(logits, y).item()  # 在这里计算训练准确率
            self.train_scores.append(trn_score)
            self.train_accuracy.append(trn_score)  # 每个epoch记录训练准确率

            # 清空梯度
            self.optimizer.zero_grad()
            # 反向传播
            trn_loss.backward()
            # 参数更新
            self.optimizer.step()

            # 验证集评估
            dev_score, dev_loss = self.evaluate(dev_set)
            if dev_score > best_score:
                print(f"[Evaluate] best accuracy performance has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
                if save_dir:
                    self.save_model(save_dir)

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}, accuracy: {trn_score:.4f}")

    def evaluate(self, data_set):
        X, y = data_set
        logits = self.model(X)
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)

        # 使用 sigmoid 计算概率
        probabilities = torch.sigmoid(logits)
        preds = (probabilities >= 0.5).float()  # 根据阈值进行预测
        score = (preds == y).float().mean().item()  # 计算准确率
        self.dev_scores.append(score)
        self.dev_accuracy.append(score)
        return score, loss

    def predict(self, X):
        return self.model(X)

    def save_model(self, save_dir):
        model_path = os.path.join(save_dir, 'D:\homework\Deep Learning\code\path')
        torch.save(self.model.state_dict(), model_path)
        print(f"Model saved to {model_path}")

    def load_model(self, model_saved_dir):
        try:
            # 加载模型参数
            self.model.load_state_dict(torch.load(model_saved_dir))
            self.model.eval()

            for layer in self.model.children():
                if isinstance(layer, torch.nn.Module):
                    params = list(layer.parameters())
                    if len(params) > 0:
                        print(f"Layer: {layer}, Parameters: {params}")

        except FileNotFoundError:
            print(f"Error: The file {model_saved_dir} does not exist.")
        except PermissionError:
            print(f"Error: Permission denied for accessing {model_saved_dir}.")
        except Exception as e:
            print(f"An unexpected error occurred: {e}")

step6 模型训练及评价

基于RunnerV2_1，使用训练集和验证集进行模型训练，共训练2000个epoch，并进行可视化。使用测试集对训练中的最优模型进行评价，观察模型的评价指标。

代码如下：

# 损失函数
loss_fn = nn.BCEWithLogitsLoss()  # 使用合适的损失函数

# 优化器
learning_rate = 0.2
optimizer = optim.SGD(model.parameters(), lr=learning_rate)


# 评价方法
metric = accuracy  # accuracy 函数可以使用 PyTorch 实现

# 实例化RunnerV2_1类，并传入训练配置
runner = RunnerV2_1(model, optimizer, metric, loss_fn)

# 训练模型
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_dir=model_saved_dir)

# 打印训练集和验证集的损失
plt.figure()
plt.plot(range(epoch_num), runner.train_loss, color="#8E004D", label="Train loss")
plt.plot(range(epoch_num), runner.dev_loss, color="#E20079", linestyle='--', label="Dev loss")
plt.xlabel("epoch", fontsize='x-large')
plt.ylabel("loss", fontsize='x-large')
plt.legend(fontsize='large')
plt.show()

# 在训练完成后保存模型
runner.save_model(model_saved_dir)

# 在测试之前加载模型
runner.load_model(model_saved_dir)

# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-math.pi, math.pi, 200), torch.linspace(-math.pi, math.pi, 200))
x = torch.stack([x1.flatten(), x2.flatten()], dim=1)

# 预测对应类别
y = runner.predict(x)
y = (y >= 0.5).float().squeeze(dim=-1)

# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:, 0].tolist(), x[:, 1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

plt.scatter(X_train[:, 0].tolist(), X_train[:, 1].tolist(), marker='*', c=y_train.squeeze(dim=-1).tolist())
plt.scatter(X_dev[:, 0].tolist(), X_dev[:, 1].tolist(), marker='*', c=y_dev.squeeze(dim=-1).tolist())
plt.scatter(X_test[:, 0].tolist(), X_test[:, 1].tolist(), marker='*', c=y_test.squeeze(dim=-1).tolist())

plt.show()

# 预测测试集
y_test_pred = runner.predict(X_test)
y_test_pred = (y_test_pred >= 0.5).float().squeeze(dim=-1)

# 计算混淆矩阵
cm = confusion_matrix(y_test.numpy(), y_test_pred.numpy())

# 绘制混淆矩阵
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=["Class 0", "Class 1"])
disp.plot(cmap=plt.cm.Blues)
plt.title("Confusion Matrix")
plt.show()

plt.figure()
epochs = range(len(runner.train_accuracy))  # 记录的训练准确率的长度
plt.plot(epochs, runner.train_accuracy, color="#8E004D", label="Train Accuracy")
plt.plot(epochs, runner.dev_accuracy[:len(epochs)], color="#E20079", linestyle='--', label="Dev Accuracy")  # 对验证准确率进行切片
plt.xlabel("Epoch", fontsize='x-large')
plt.ylabel("Accuracy", fontsize='x-large')
plt.legend(fontsize='large')
plt.title("Accuracy Curve")
plt.show()

训练过程部分如下：

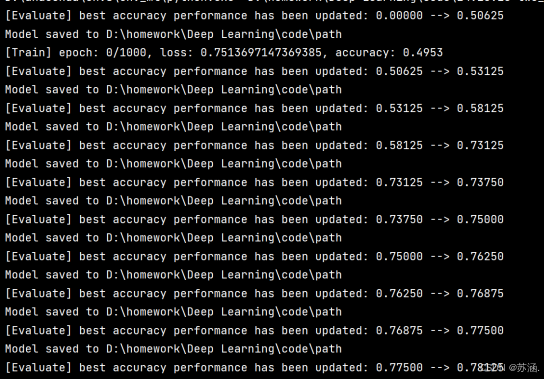
这里不知道为什么训练数据集的准确率一直不变，还没有找出来到底哪里出了问题。o(╥﹏╥)o

损失变化曲线和准确率变化曲线如下：（先挂在这里，后面会进行更改）

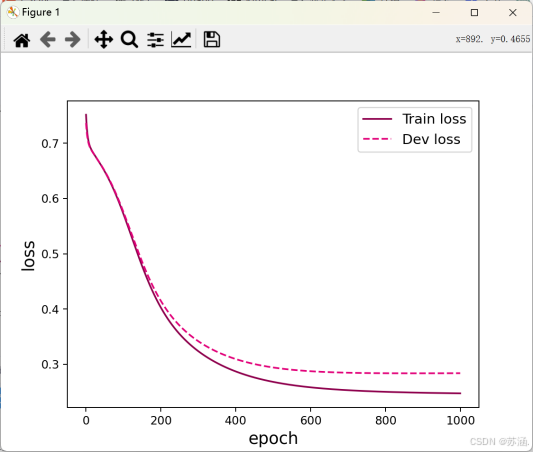
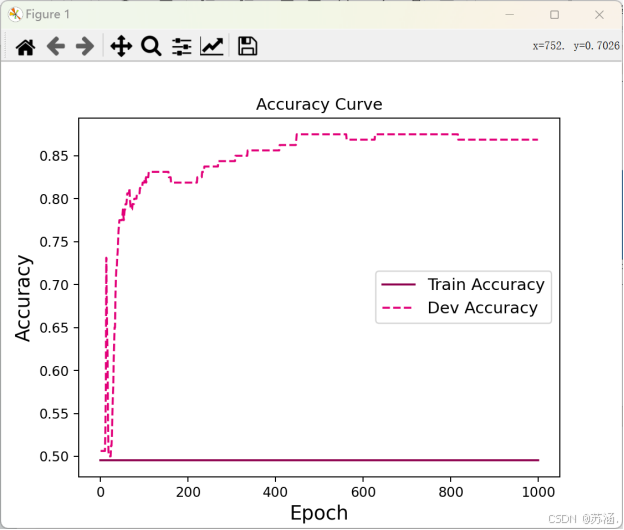
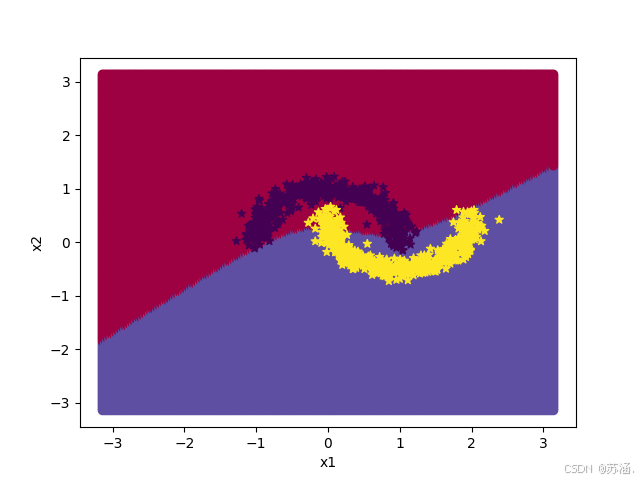
边界图和混淆矩阵如下：

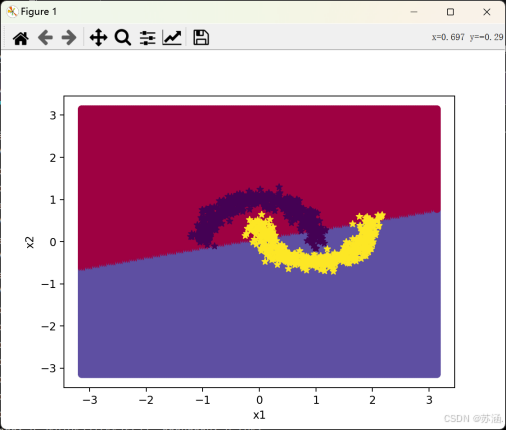
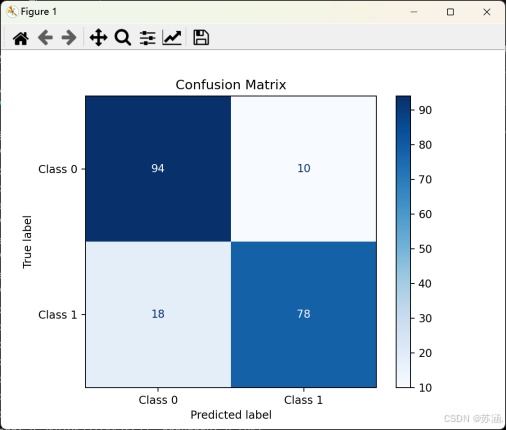
注：

1.运行代码时出现了一个从来没见过的一个错误：

OMP:错误#15:正在初始化libiomp5md.dll，但发现libiomp5md.dll已经初始化。

室友让我把.dll这个镜像文件删了，但是有点不太敢删，因为上次就是因为彻底删除镜像文件导致我的电脑不能用了，只能重装系统。（我不是没有重装系统和重装Python的勇气！）所以上网找资料，发现加入这行代码就可以了：

“os.environ['KMP_DUPLICATE_LIB_OK'] = 'True'”

这个环境变量通常用于解决使用 Intel 的 Math Kernel Library (MKL) 时可能遇到的问题。当存在多个 MKL 库实例加载到同一个进程中时，会出现冲突的情况。设置 `KMP_DUPLICATE_LIB_OK` 为 `'True'` 允许库继续执行即使检测到在同一进程中加载了多个库实例，因此是指"允许重复加载库"。

2.学长的实验运行结果比我这个要好很多很多：

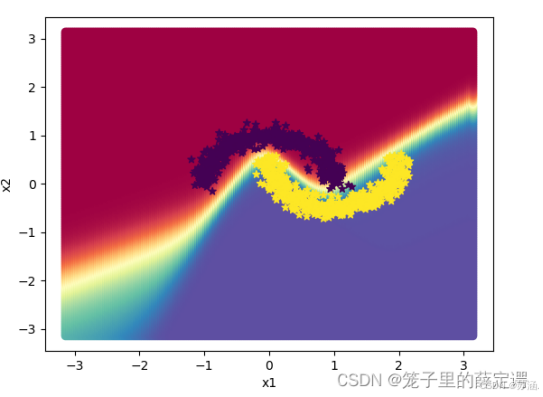
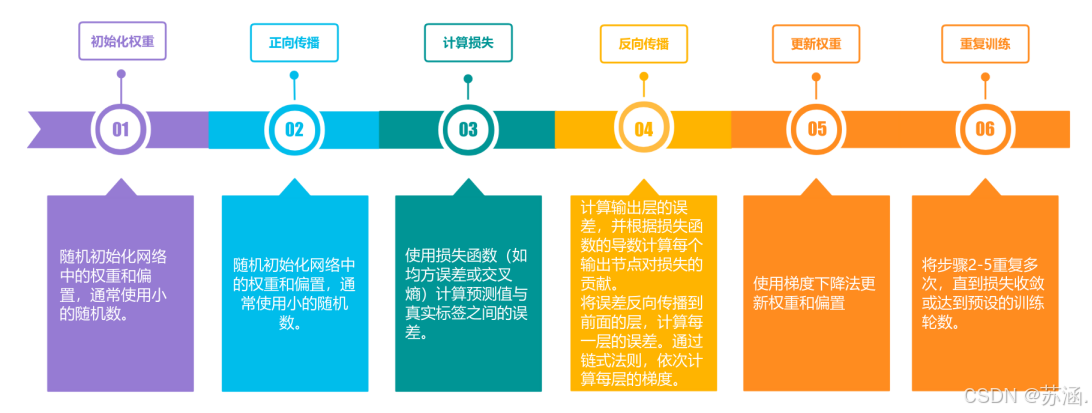
3.前馈神经网络的参数梯度通常使用误差反向传播算法来计算，下图为使用误差反向传播算法的前馈神经网络训练过程的步骤

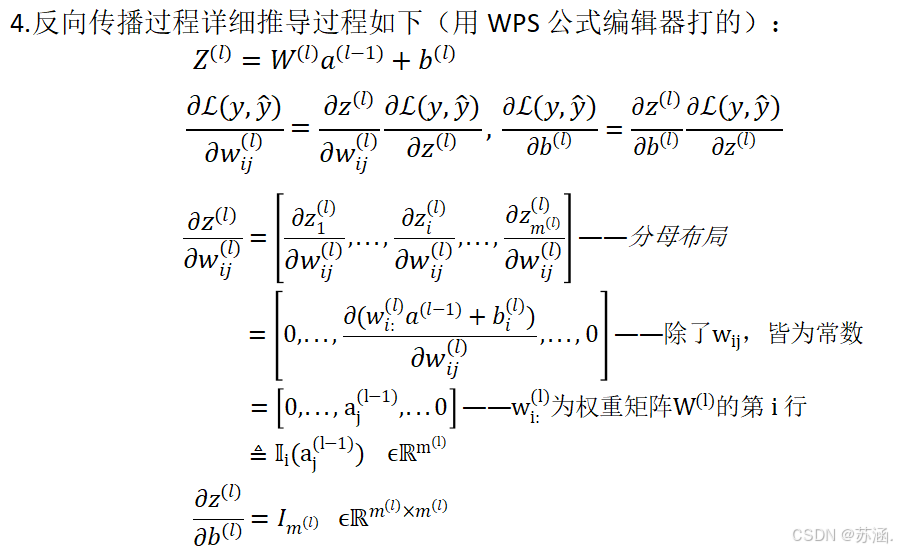
5.对比“基于Logistic回归的二分类任务”与“基于前馈神经网络的二分类任务”：Logistic回归简单易懂，适合线性可分的数据，模型训练速度快且易于解释。然而，它在处理复杂模式时表现有限，难以捕捉非线性关系。前馈神经网络则更为灵活，能够通过多层结构捕捉复杂的非线性关系。尽管其表达能力更强，但训练过程较为复杂，需要调整更多的超参数，并且对数据量和计算资源的要求更高。而且实现起来很困难。

更新！！！

找到错误在哪里了！！

原来是隐藏层的个数没有设置好，实验书上写的是5，所以我就直接用的5，跑出来的结果就怪怪的┭┮﹏┭┮。后面把他设置成了100，结果出乎意料的好哇！(#^.^#) 我的决策边界也可以弯曲了！

大家在试的时候也要注意这个问题，一定要注重参数的重要性！

附完整代码（uu们可以运行试一试）：

import math
import os
import numpy as np
import paddle
import torch
from matplotlib import pyplot as plt
from sklearn.datasets import make_moons
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from torch import nn, optim

import nndl
from Two_class import accuracy
from nndl import Model_MLP_L2  # 假设 Model_MLP_L2 已在 PyTorch 中实现

os.environ['KMP_DUPLICATE_LIB_OK'] = 'True'

# 构建数据集
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.1)

# 将 y 转换为 Tensor
y = torch.FloatTensor(y).reshape([-1, 1])

# 可视化生成的数据集，不同颜色代表不同类别
plt.figure(figsize=(5, 5))
plt.scatter(x=X[:, 0], y=X[:, 1], marker='*', c=y.numpy())
plt.show()

# 划分数据集, 640条训练集，160条验证集，200条测试集
num_train = 640
num_dev = 160
num_test = 200
X_train, y_train = torch.FloatTensor(X[:num_train]), y[:num_train]
X_dev, y_dev = torch.FloatTensor(X[num_train:num_train + num_dev]), y[num_train:num_train + num_dev]
X_test, y_test = torch.FloatTensor(X[num_train + num_dev:]), y[num_train + num_dev:]

# 实例化模型
model = Model_MLP_L2(input_size=5, hidden_size=10, output_size=1)


# 实现交叉熵损失函数
def cross_entropy_loss(y_pred, y_true):
    # 为了避免 log(0)，增加一个小值 eps
    eps = 1e-10
    y_pred = torch.clamp(y_pred, eps, 1.0 - eps)
    # 计算交叉熵损失
    loss = -torch.mean(y_true * torch.log(y_pred) + (1 - y_true) * torch.log(1 - y_pred))
    return loss


# 基础优化器类
class Optimizer(object):
    def __init__(self, model, init_lr=0.1):
        # 保存模型对象
        self.init_lr = init_lr
        self.model = model

    def step(self):
        raise NotImplementedError("Subclasses should implement this method.")


class BatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(BatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        # 参数更新
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
                for key in layer.params.keys():
                    # 假设 layer.grads 存在并已经计算了每一层的梯度
                    layer.params[key] = layer.params[key] - self.init_lr * layer.grads[key]


# 完善Runner类
class RunnerV2_1(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

        # 记录准确率
        self.train_accuracy = []
        self.dev_accuracy = []

    def accuracy(y_pred, y_true):
        y_pred_labels = (torch.sigmoid(y_pred) >= 0.5).float()  # 根据阈值进行预测
        return (y_pred_labels == y_true).float().mean()

    def train(self, train_set, dev_set, save_dir=None, probabilities=None, **kwargs):
        num_epochs = kwargs.get("num_epochs", 0)
        log_epochs = kwargs.get("log_epochs", 100)

        best_score = 0
        for epoch in range(num_epochs):
            X, y = train_set
            logits = self.model(X)

            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)
            self.train_loss.append(trn_loss.item())

            # 计算训练准确率
            trn_score = self.metric(logits, y).item()  # 在这里计算训练准确率
            self.train_scores.append(trn_score)
            self.train_accuracy.append(trn_score)  # 每个epoch记录训练准确率

            # 清空梯度
            self.optimizer.zero_grad()
            # 反向传播
            trn_loss.backward()
            # 参数更新
            self.optimizer.step()

            # 验证集评估
            dev_score, dev_loss = self.evaluate(dev_set)
            if dev_score > best_score:
                print(f"[Evaluate] best accuracy performance has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
                if save_dir:
                    self.save_model(save_dir)

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}, accuracy: {trn_score:.4f}")

    def evaluate(self, data_set):
        X, y = data_set
        logits = self.model(X)
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)

        # 使用 sigmoid 计算概率
        probabilities = torch.sigmoid(logits)
        preds = (probabilities >= 0.5).float()  # 根据阈值进行预测
        score = (preds == y).float().mean().item()  # 计算准确率
        self.dev_scores.append(score)
        self.dev_accuracy.append(score)
        return score, loss

    def predict(self, X):
        return self.model(X)

    def save_model(self, save_dir):
        model_path = os.path.join(save_dir, 'D:\homework\Deep Learning\code\path')
        torch.save(self.model.state_dict(), model_path)
        print(f"Model saved to {model_path}")

    def load_model(self, model_saved_dir):
        try:
            # 加载模型参数
            self.model.load_state_dict(torch.load(model_saved_dir))
            self.model.eval()

            for layer in self.model.children():
                if isinstance(layer, torch.nn.Module):
                    params = list(layer.parameters())
                    if len(params) > 0:
                        print(f"Layer: {layer}, Parameters: {params}")

        except FileNotFoundError:
            print(f"Error: The file {model_saved_dir} does not exist.")
        except PermissionError:
            print(f"Error: Permission denied for accessing {model_saved_dir}.")
        except Exception as e:
            print(f"An unexpected error occurred: {e}")


# 设置随机种子
torch.manual_seed(123)
epoch_num = 1000

model_saved_dir = "model"

# 输入层维度为2
input_size = 2
# 隐藏层维度为5
hidden_size = 7
# 输出层维度为1
output_size = 1


# 定义网络
class Model_MLP_L2(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.act_fn1 = nn.Sigmoid()
        self.fc2 = nn.Linear(hidden_size, output_size)

    def forward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        return z2  # 输出 logits 而不是经过 Sigmoid 的值


model = Model_MLP_L2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 损失函数
loss_fn = nn.BCEWithLogitsLoss()  # 使用合适的损失函数

# 优化器
learning_rate = 0.2
optimizer = optim.SGD(model.parameters(), lr=learning_rate)


# 评价方法
metric = accuracy  # accuracy 函数可以使用 PyTorch 实现

# 实例化RunnerV2_1类，并传入训练配置
runner = RunnerV2_1(model, optimizer, metric, loss_fn)

# 训练模型
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_dir=model_saved_dir)

# 打印训练集和验证集的损失
plt.figure()
plt.plot(range(epoch_num), runner.train_loss, color="#8E004D", label="Train loss")
plt.plot(range(epoch_num), runner.dev_loss, color="#E20079", linestyle='--', label="Dev loss")
plt.xlabel("epoch", fontsize='x-large')
plt.ylabel("loss", fontsize='x-large')
plt.legend(fontsize='large')
plt.show()

# 在训练完成后保存模型
runner.save_model(model_saved_dir)

# 在测试之前加载模型
runner.load_model(model_saved_dir)

# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-math.pi, math.pi, 200), torch.linspace(-math.pi, math.pi, 200))
x = torch.stack([x1.flatten(), x2.flatten()], dim=1)

# 预测对应类别
y = runner.predict(x)
y = (y >= 0.5).float().squeeze(dim=-1)

# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:, 0].tolist(), x[:, 1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

plt.scatter(X_train[:, 0].tolist(), X_train[:, 1].tolist(), marker='*', c=y_train.squeeze(dim=-1).tolist())
plt.scatter(X_dev[:, 0].tolist(), X_dev[:, 1].tolist(), marker='*', c=y_dev.squeeze(dim=-1).tolist())
plt.scatter(X_test[:, 0].tolist(), X_test[:, 1].tolist(), marker='*', c=y_test.squeeze(dim=-1).tolist())

plt.show()

# 预测测试集
y_test_pred = runner.predict(X_test)
y_test_pred = (y_test_pred >= 0.5).float().squeeze(dim=-1)

# 计算混淆矩阵
cm = confusion_matrix(y_test.numpy(), y_test_pred.numpy())

# 绘制混淆矩阵
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=["Class 0", "Class 1"])
disp.plot(cmap=plt.cm.Blues)
plt.title("Confusion Matrix")
plt.show()

plt.figure()
epochs = range(len(runner.train_accuracy))  # 记录的训练准确率的长度
plt.plot(epochs, runner.train_accuracy, color="#8E004D", label="Train Accuracy")
plt.plot(epochs, runner.dev_accuracy[:len(epochs)], color="#E20079", linestyle='--', label="Dev Accuracy")  # 对验证准确率进行切片
plt.xlabel("Epoch", fontsize='x-large')
plt.ylabel("Accuracy", fontsize='x-large')
plt.legend(fontsize='large')
plt.title("Accuracy Curve")
plt.show()

nndl的代码：

import math
from abc import abstractmethod

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F


# 定义基础操作类
class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        raise NotImplementedError

    def backward(self, inputs):
        raise NotImplementedError


# 实现线性层算子
class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=np.random.standard_normal, bias_init=torch.zeros):
        super().__init__()
        self.params = {}
        self.params['W'] = weight_init([input_size, output_size])
        self.params['W'] = torch.as_tensor(self.params['W'], dtype=torch.float32)
        self.params['b'] = bias_init([1, output_size])

        self.inputs = None
        self.grads = {}

        self.name = name

    def forward(self, inputs):
        self.inputs = inputs
        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

    def backward(self, grads):
        self.grads['W'] = torch.matmul(self.inputs.T, grads)
        self.grads['b'] = torch.sum(grads, dim=0)

        # 线性层输入的梯度
        return torch.matmul(grads, self.params['W'].T)


# 实现 Logistic 激活函数
class Logistic(Op):
    def __init__(self):
        super().__init__()
        self.inputs = None
        self.outputs = None
        self.params = None

    def forward(self, inputs):
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

    def backward(self, grads):
        # 计算Logistic激活函数对输入的导数
        outputs_grad_inputs = torch.multiply(self.outputs, (1.0 - self.outputs))
        return torch.multiply(grads, outputs_grad_inputs)


# 定义多层感知机模型（MLP）带L2正则化
# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        # 线性层
        super().__init__()
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        # Logistic激活函数层
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

        self.layers = [self.fc1, self.act_fn1, self.fc2, self.act_fn2]

    def __call__(self, X):
        return self.forward(X)

    # 前向计算
    def forward(self, X):
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2

    # 反向计算
    def backward(self, loss_grad_a2):
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)


# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
    def __init__(self, model):
        super().__init__()
        self.predicts = None
        self.labels = None
        self.num = None

        self.model = model

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts))
                                 + torch.matmul((1 - self.labels.t()), torch.log(1 - self.predicts)))

        loss = torch.squeeze(loss, axis=1)
        return loss

    def backward(self):
        # 计算损失函数对模型预测的导数
        loss_grad_predicts = -1.0 * (self.labels / self.predicts -
                                     (1 - self.labels) / (1 - self.predicts)) / self.num

        # 梯度反向传播
        self.model.backward(loss_grad_predicts)


def make_moons(n_samples=1000, shuffle=True, noise=None):
    n_samples_out = n_samples // 2
    n_samples_in = n_samples - n_samples_out

    outer_circ_x = torch.cos(torch.linspace(0, math.pi, n_samples_out))
    outer_circ_y = torch.sin(torch.linspace(0, math.pi, n_samples_out))

    inner_circ_x = 1 - torch.cos(torch.linspace(0, math.pi, n_samples_in))
    inner_circ_y = 0.5 - torch.sin(torch.linspace(0, math.pi, n_samples_in))

    print('outer_circ_x.shape:', outer_circ_x.shape, 'outer_circ_y.shape:', outer_circ_y.shape)
    print('inner_circ_x.shape:', inner_circ_x.shape, 'inner_circ_y.shape:', inner_circ_y.shape)

    X = torch.stack(
        [torch.cat([outer_circ_x, inner_circ_x]),
         torch.cat([outer_circ_y, inner_circ_y])],
        axis=1
    )

    print('after concat shape:', torch.cat([outer_circ_x, inner_circ_x]).shape)
    print('X shape:', X.shape)

    # 使用'torch. zeros'将第一类数据的标签全部设置为0
    # 使用'torch. ones'将第一类数据的标签全部设置为1
    y = torch.cat(
        [torch.zeros([n_samples_out]), torch.ones([n_samples_in])]
    )

    print('y shape:', y.shape)

    # 如果shuffle为True，将所有数据打乱
    if shuffle:
        # 使用'torch.randperm'生成一个数值在0到X.shape[0]，随机排列的一维Tensor做索引值，用于打乱数据
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]

    # 如果noise不为None，则给特征值加入噪声
    if noise is not None:
        X += np.random.normal(0.0, noise, X.shape)

    return X, y


# 新增优化器基类
class Optimizer(object):
    def __init__(self, init_lr, model):
        # 初始化学习率，用于参数更新的计算
        self.init_lr = init_lr
        # 指定优化器需要优化的模型
        self.model = model

    @abstractmethod
    def step(self):
        pass


class BatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(BatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        # 参数更新
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
                for key in layer.params.keys():
                    layer.params[key] = layer.params[key] - self.init_lr * layer.grads[key]

参考文献：

[1]OMP: Error #15: Initializing libiomp5md.dll, but found libiomp5md.dll already initialized.-CSDN博客

[2]NNDL 实验五前馈神经网络（1）二分类任务_nndl实验前馈神经网络-CSDN博客

[3]飞桨AI Studio星河社区-人工智能学习与实训社区

本次的分享就到这里，有错误希望uu们提醒，期待下次再见~(#^.^#)