SHAP 可解释性竟然还能做聚类分析?ExplaineR 包带你从机器学习建模到特征重要性一网打尽,兼顾可视化美图!
从二分类建模、评估、SHAP可解释性甚至到。
生信碱移
ExplaineR包
模型构建到解释的方方面面,你甚至可以用SHAP做聚类(患者亚型分析)。
近年来,机器学习在处理临床数据集中的应用变得越来越流行。然而,随着新复杂算法的引入,理解这些算法如何产生输出成为了一个挑战。例如,基于树的集成模型(如随机森林)和梯度提升机具有强大的预测能力,但可解释性有限。
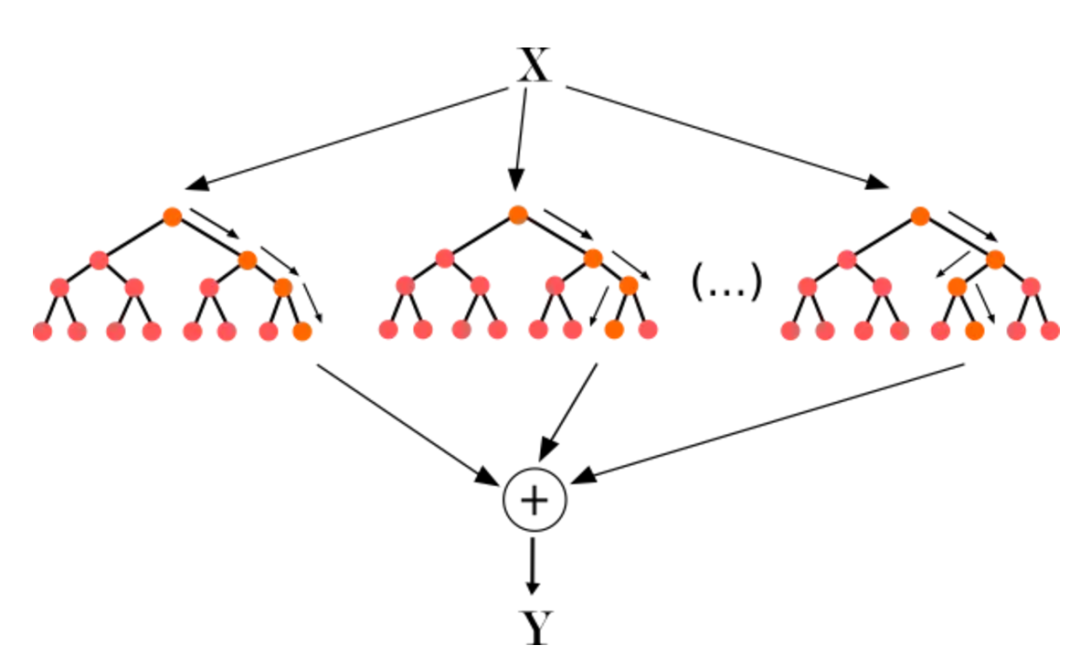
▲ 随机森林的示意图,本质上是集成和自助,多个随机变量的决策树给出最后综合的预测结果。随机森林通过Gini重要性来衡量一个特征在决策树中有多频繁地被用于分裂数据,越频繁的特征则是越重要的。关于决策树与随机森林的原理及代码讲解可以点击上方图片跳转。
现有的方法在从这些模型中提取特征重要性时存在局限性,导致特征重要性评估的不一致性。例如,Gini重要性度量(通过特征分割数据的频率来确定特征的重要性)倾向于高估连续变量或高基数类别变量的重要性,而低估相关特征的重要性。SHAP可解释性分析基于合作博弈论,已成为提高模型可解释性的一个重要工具。它量化了每个特征对模型预测的贡献,有助于解释复杂模型的决策。
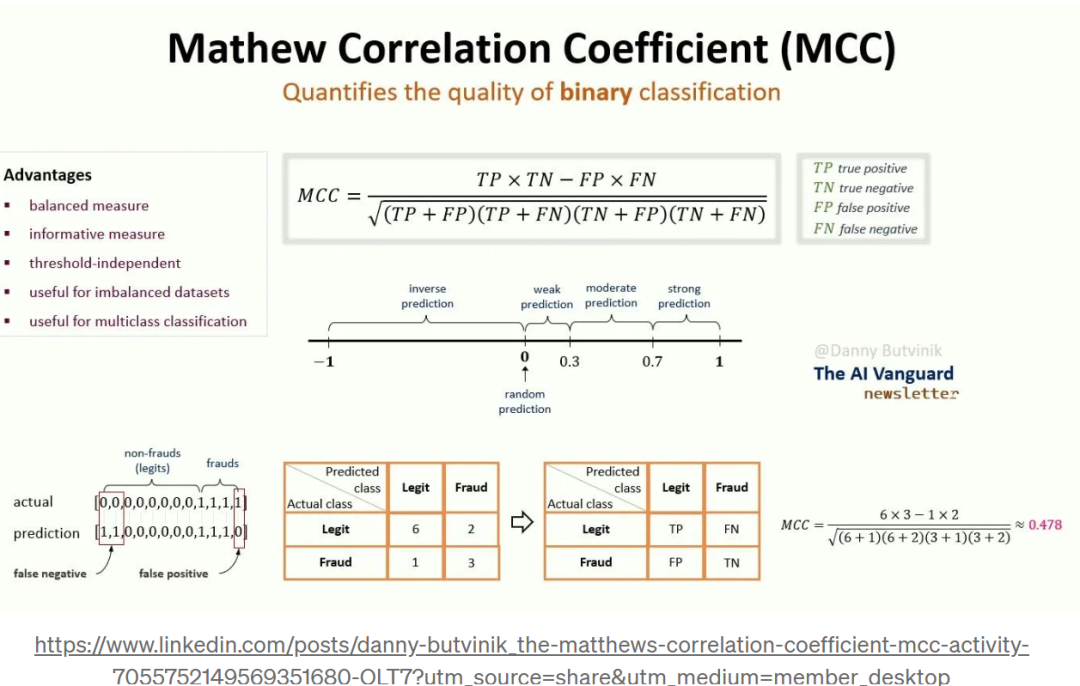
▲ Matthews相关系数(Matthews correlation coefficient, MCC) 是一种用于二元分类问题的性能度量,尤其在类别不平衡的情况下非常有效。它结合了四个主要的分类结果:真正例(True Positives, TP)、假正例(False Positives, FP)、真负例(True Negatives, TN)和假负例(False Negatives, FN)。
在可视化层面,尽管模型性能度量(如二元分类中的Matthews相关系数)对评估模型至关重要,但这些度量通常在SHAP总结图中被忽视。此外,像决策曲线分析这样的可视化工具也对理解模型性能至关重要,但有时会被忽略。为了应对这些挑战,来自哥本哈根医学院的研究者引入了ExplaineR包,旨在提供一个全面的框架来解释机器学习模型,特别是针对二元分类和回归模型。该包旨在标准化模型性能和解释报告,便于在医学和临床科学等领域的广泛应用。

▲ ExplaineR工作流程。作者展示了使用ExplaineR包进行机器学习分析的工作流程,基于威斯康星乳腺癌数据集进行的随机森林(Random Forest)二元分类模型分析。左侧面板展示了训练集和测试集的混淆矩阵,以及模型净收益与替代方案的比较图。右侧面板则展示了通过SHAP聚类得到的三个样本群体的SHAP总结图及其对应的混淆矩阵。
本文简要介绍ExplaineR的使用,从二分类建模、评估、SHAP可解释性甚至到可解释性聚类,可以说这个R包能做的东西还是非常全面的。感兴趣多分类或者回归的老铁,可以参考下方链接:
-
https://persimune.github.io/explainer/index.html
-
https://github.com/PERSIMUNE/explainer/
R包安装
可以使用以下代码从CRAN安装该包:
install.packages("explainer")
也可以安装Github中的更新版本:
# install.packages("devtools")
devtools::install_github("PERSIMUNE/explainer")
使用示例(共9点)
① 加载数据集并训练机器学习模型。以下代码加载了一个乳腺癌数据集并创建了一个二元分类任务,然后使用mlr3包训练了一个"随机森林"模型。
Sys.setenv(LANG = "en") # change R language to English!
RNGkind("L'Ecuyer-CMRG") # change to L'Ecuyer-CMRG in case it uses default "Mersenne-Twister"
library("explainer")
# 创建随机数种子,使结果可重复
seed <- 246
set.seed(seed)
# 从mlbench包中加载数据集
data("BreastCancer", package = "mlbench")
# 确定预测目标列名
target_col <- "Class"
# 将"malignant"设置为阳性样本
positive_class <- "malignant"
# 删除无用数据
mydata <- BreastCancer[, -1] # 1 is ID
# 移除na
mydata <- na.omit(mydata)
# 创建性别分组
sex <- sample(c("Male", "Female"), size = nrow(mydata), replace = TRUE)
mydata$age <- as.numeric(sample(seq(18,60), size = nrow(mydata), replace = TRUE))
# 添加一列性别用于公平性分析,确保模型不对特定群体(如种族、性别、年龄、收入等)产生区别的影响
mydata$sex <- factor(sex, levels = c("Male", "Female"), labels = c(1, 0))
# 创建一个分类任务
maintask <- mlr3::TaskClassif$new(id = "my_classification_task",
backend = mydata,
target = target_col,
positive = positive_class)
# 分割生成训练与测试
set.seed(seed)
splits <- mlr3::partition(maintask)
library("mlr3learners")
接下来,进行模型训练与测试:
mylrn <- mlr3::lrn("classif.ranger", predict_type = "prob")
# 训练模型
mylrn$train(maintask, splits$train)
# 测试上进行预测
mylrn$predict(maintask, splits$test)
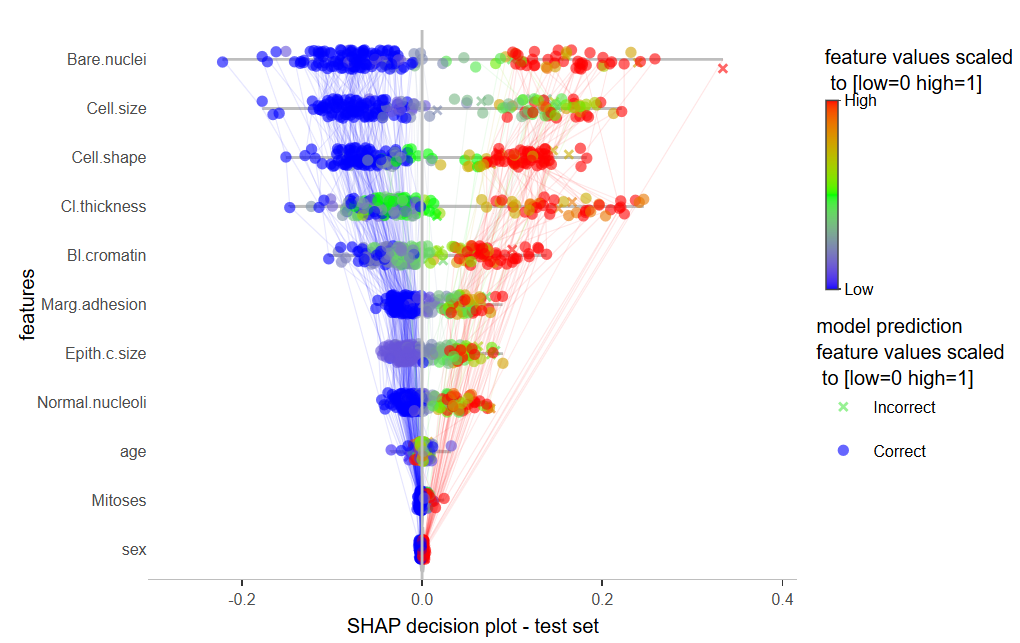
② 使用SHAP分析特征变量对预测的影响:
library("magrittr")
library("plotly")
# enhanced SHAP plot
SHAP_output <- eSHAP_plot(task = maintask,
trained_model = mylrn,
splits = splits,
sample.size = 30,
seed = seed,
subset = .8)
# 可视化
myplot <- SHAP_output[[1]]
myplot
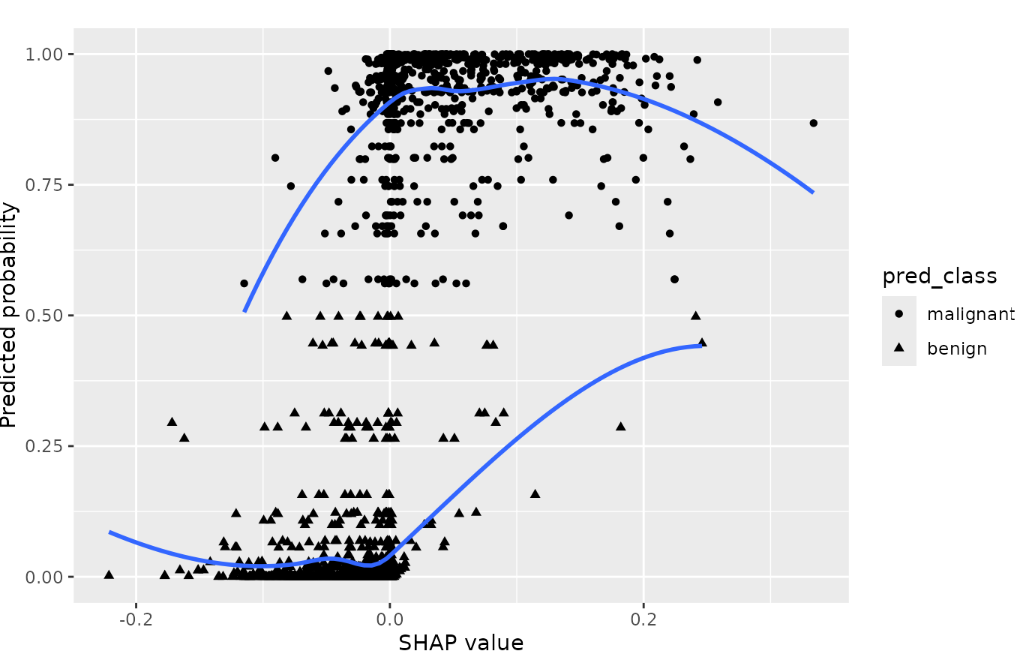
可视化与预测概率相关的SHAP值:
SHAP_output[[5]]
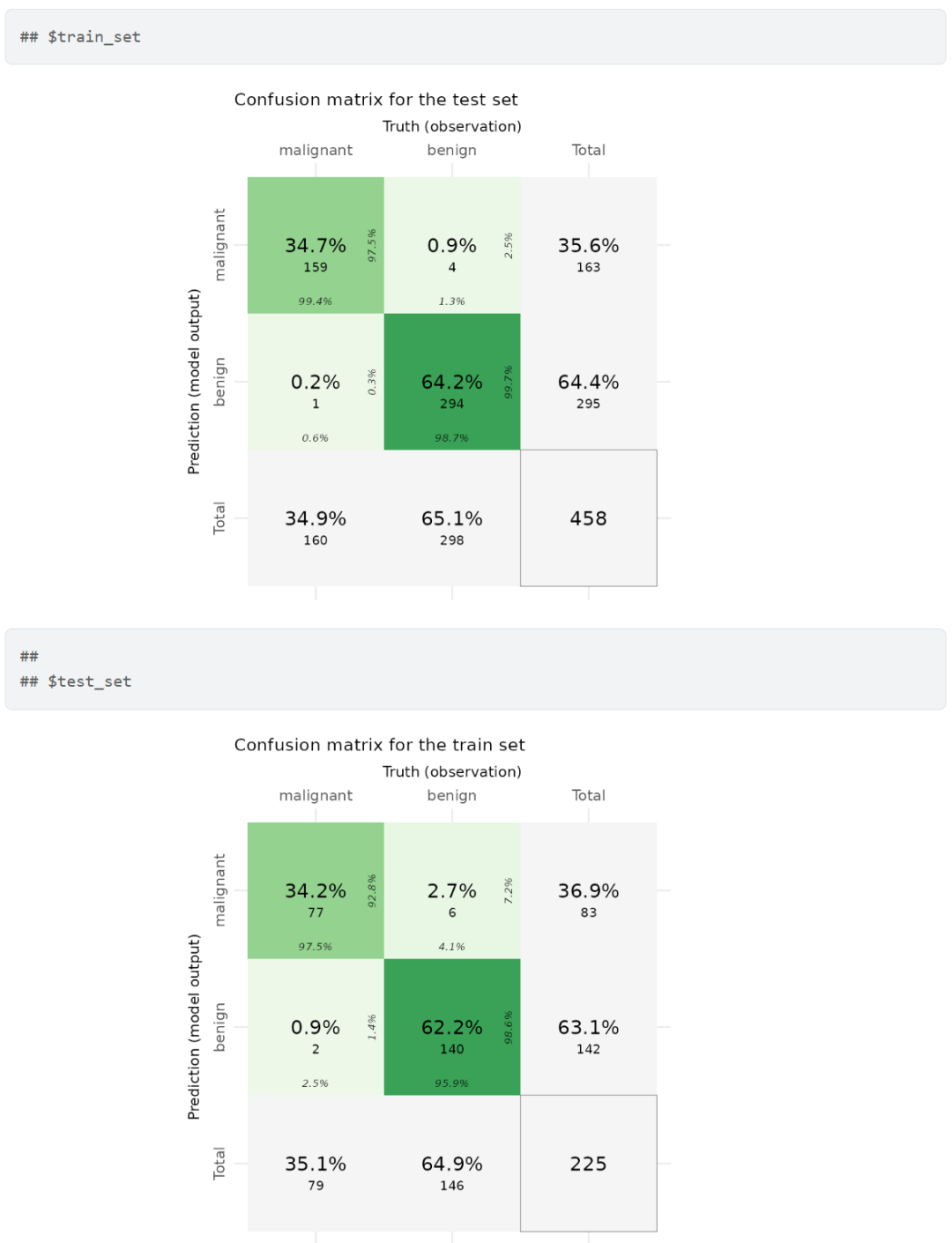
③ 通过混淆矩阵可视化模型性能。下列代码段使用eCM_plot函数可视化混淆矩阵,以评估训练和测试集的模型性能:
# enhanced confusion matrix
confusionmatrix_plot <- eCM_plot(task = maintask,
trained_model = mylrn,
splits = splits)
#可视化
print(confusionmatrix_plot)
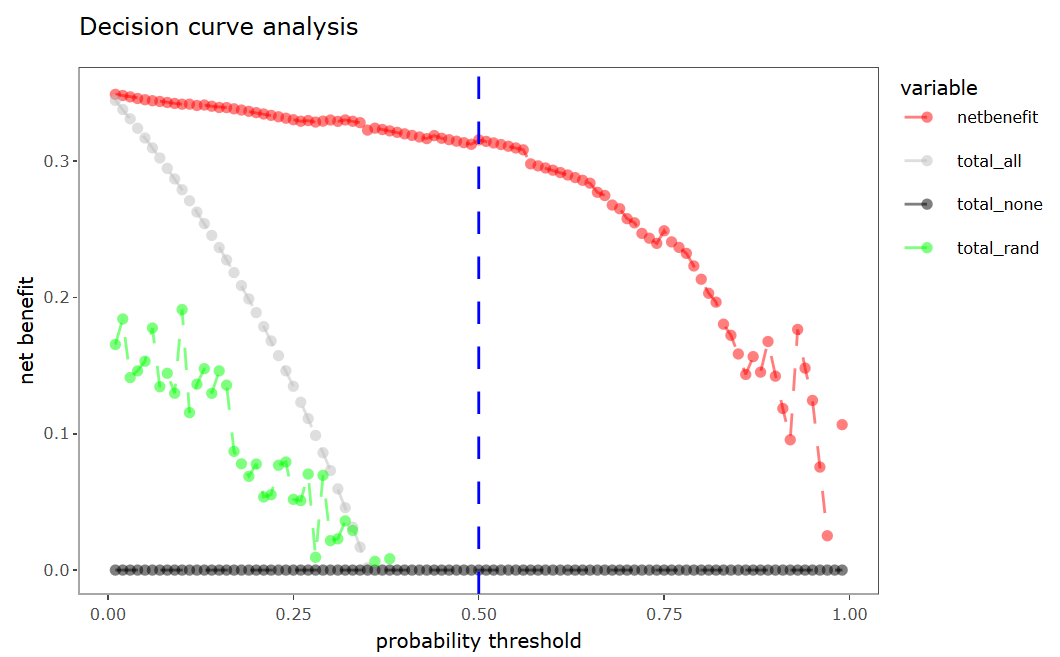
④ 决策曲线分析。采用eDecisionCurve函数对模型中的测试集进行"决策曲线分析":
# enhanced decision curve plot
eDecisionCurve(task = maintask,
trained_model = mylrn,
splits = splits,
seed = seed)
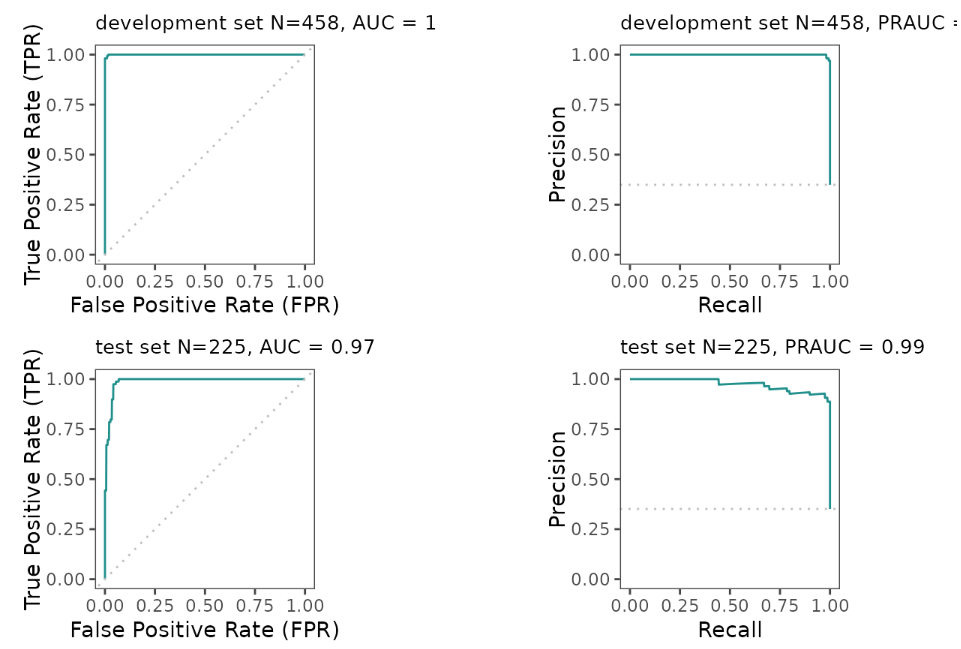
⑤ 模型评估(多指标和ROC曲线绘制),该包提供的模型评估和可视化指标包括:
-
ROC曲线下面积(AUC): AUC量化了二元分类模型的性能,方法是评估 ROC 曲线下的面积,该曲线绘制了不同阈值下的灵敏度与1-特异度。0.5的值表示随机表现,而1表示完美分类;
-
平衡准确度(BACC):BACC通过平均敏感度和特异性来解决类别不平衡问题。范围从0到1,0分表示偶然表现,1分表示完美分类;
-
马修斯相关系数(MCC):MCC评估二分类模型质量,考虑真阳性、真阴性、假阳性和假阴性。范围从-1到1,-1表示完全不一致,0表示随机性能,1表示完美分类;
-
布里尔得分(BBRIER): 布里尔得分通过测量预测概率和实际二元结果之间的平均平方差来衡量概率预测的准确性。取值范围从0到1,越大越好;
-
正确率(PPV):PPV或准确率,衡量模型所有正预测中真正属于正类的比例;
-
负预测值(NPV): NPV量化了模型做出的全部负预测中真正为负的预测的比例;
-
特异性(Specificity):特异性计算在二分类问题中,所有实际负例中真正的负预测的比例;
-
敏感度(Sensitivity): 也称为召回率或真正率,衡量二元分类问题中所有实际阳性案例中真正阳性预测的比例;
-
准确率-召回率曲线下面积(PRAUC):PRAUC根据精确度和召回率评估二元分类模型的性能,量化了精确率-召回率曲线下的面积。PRAUC值为1表示分类性能完美。除了以上得分的计算,还可以可视化训练集和测试集的ROC和PR曲线:
eROC_plot(task = maintask,
trained_model = mylrn,
splits = splits)
## [[1]]
# 输出图片在下面
##
## [[2]]
## pred_results$score(measures = mlr3::msrs(meas))
## auc 1.00
## bacc 0.99
## mcc 0.98
## bbrier 0.01
## ppv 0.98
## npv 1.00
## specificity 0.99
## sensitivity 0.99
## prauc 1.00
##
## [[3]]
## pred_results_test$score(measures = mlr3::msrs(meas))
## auc 0.99
## bacc 0.97
## mcc 0.92
## bbrier 0.04
## ppv 0.93
## npv 0.99
## specificity 0.96
## sensitivity 0.97
## prauc 0.97
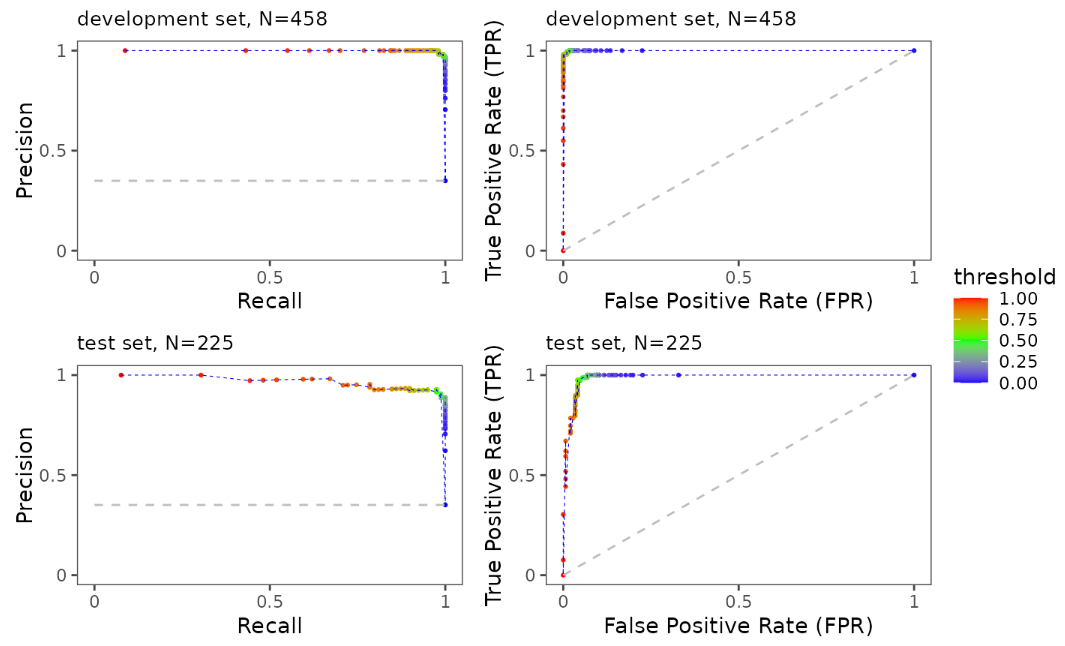
不仅如此,可以指定带有注释的阈值ROC曲线(即不同概率阈值下的模型精准性与召回率):
ePerformance(task = maintask,
trained_model = mylrn,
splits = splits)
⑥ 进一步加载SHAP结果以供后续分析。首先,可以从eSHAP_plot函数获得输出来对SHAP值应用聚类:
shap_Mean_wide <- SHAP_output[[2]]
shap_Mean_long <- SHAP_output[[3]]
shap <- SHAP_output[[4]]
其次,可以分析SHAP值与特征变量之间的关联:
ShapFeaturePlot(shap_Mean_long)
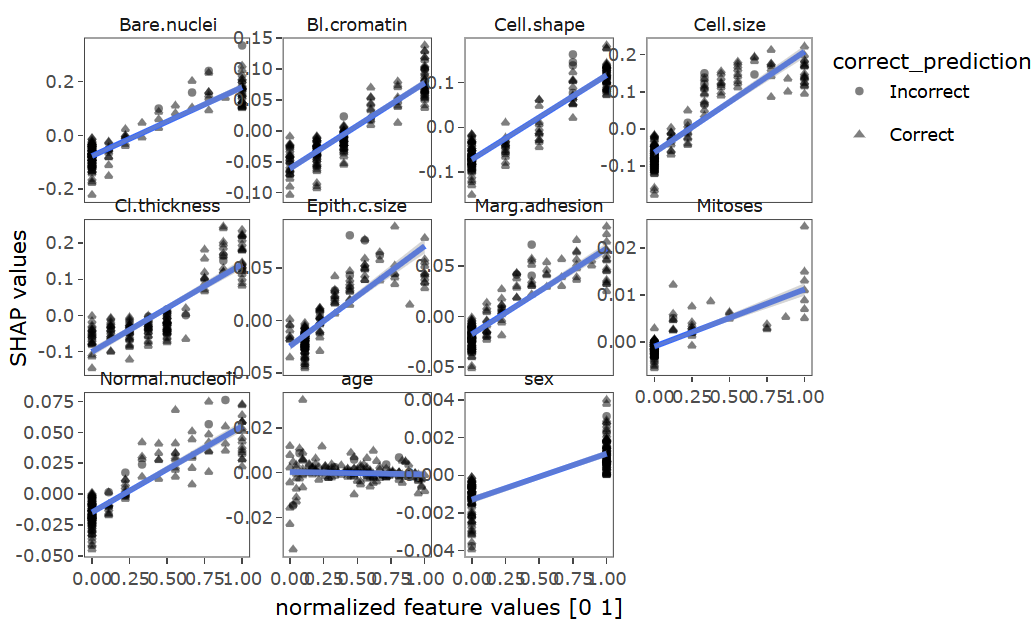
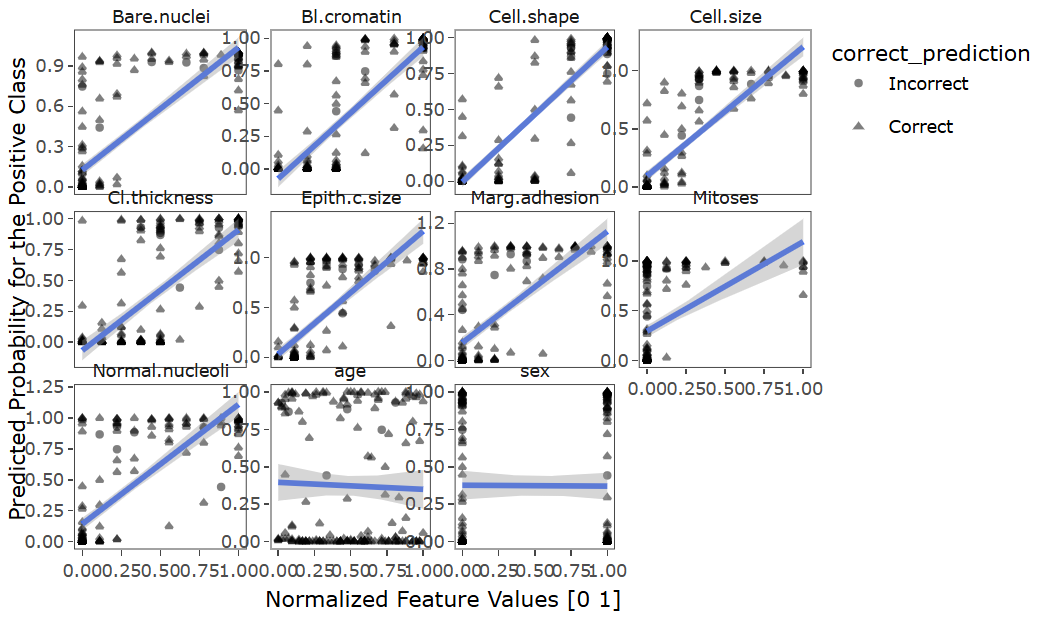
再者,可以绘制偏依赖图 (PDPs),用于可视化单个特征对模型预测的边际效应。具体而言,PDP是一种可视化工具,旨在展示一个或多个特征的变化如何影响预测模型的输出。PDP显示了某个特定特征的变化对模型预测结果的影响,假设其他特征保持不变:
ShapPartialPlot(shap_Mean_long = shap_Mean_long)
⑦ 由SHAP聚类确定患者的亚型。SHAP聚类是一种方法,用于更好地理解为何模型对某些患者的表现优于其他患者。例如,可以识别出具有特定特征模式的患者亚型,从而解释为何模型在这些患者上的表现优于或劣于整个数据集的平均表现。在SHAP图中,如果将所有样本合并,会得到整体的SHAP总结图。这里的边缘反映了特征在每个单独样本中的相互作用。
# num_of_clusters参数指定聚类数量
SHAP_plot_clusters <- SHAPclust(task = maintask,
trained_model = mylrn,
splits = splits,
shap_Mean_wide = shap_Mean_wide,
shap_Mean_long = shap_Mean_long,
num_of_clusters = 3,
seed = seed,
subset = .8)
## Key: <sample_num, feature, Phi>
## sample_num feature Phi cluster mean_phi f_val
## <int> <char> <num> <int> <num> <num>
## 1: 1 Bare.nuclei -0.0858948677 3 0.093444244 0.0000000
## 2: 1 Bl.cromatin -0.0699857672 3 0.044548987 0.0000000
## 3: 1 Cell.shape -0.0459229894 3 0.076720237 0.0000000
## 4: 1 Cell.size -0.0555791270 3 0.091198097 0.0000000
## 5: 1 Cl.thickness -0.0169917196 3 0.069835393 0.5000000
## ---
## 1976: 180 Marg.adhesion 0.0475544444 2 0.026453762 1.0000000
## 1977: 180 Mitoses 0.0024593386 2 0.002165296 0.1250000
## 1978: 180 Normal.nucleoli 0.0348163757 2 0.021391343 0.7777778
## 1979: 180 age -0.0157181481 2 0.003230698 0.0000000
## 1980: 180 sex -0.0008616667 2 0.001183048 0.0000000
## unscaled_f_val correct_prediction pred_prob pred_class
## <num> <fctr> <num> <fctr>
## 1: 1 Correct 0.002554762 benign
## 2: 1 Correct 0.002554762 benign
## 3: 1 Correct 0.002554762 benign
## 4: 1 Correct 0.002554762 benign
## 5: 5 Correct 0.002554762 benign
## ---
## 1976: 10 Correct 0.926616667 malignant
## 1977: 2 Correct 0.926616667 malignant
## 1978: 8 Correct 0.926616667 malignant
## 1979: 18 Correct 0.926616667 malignant
## 1980: 1 Correct 0.926616667 malignant
如上,cluster列即为聚类结果。接下来可以将聚类与SHAP一起进行可视化:
# display the SHAP cluster plots
SHAP_plot_clusters[[1]]
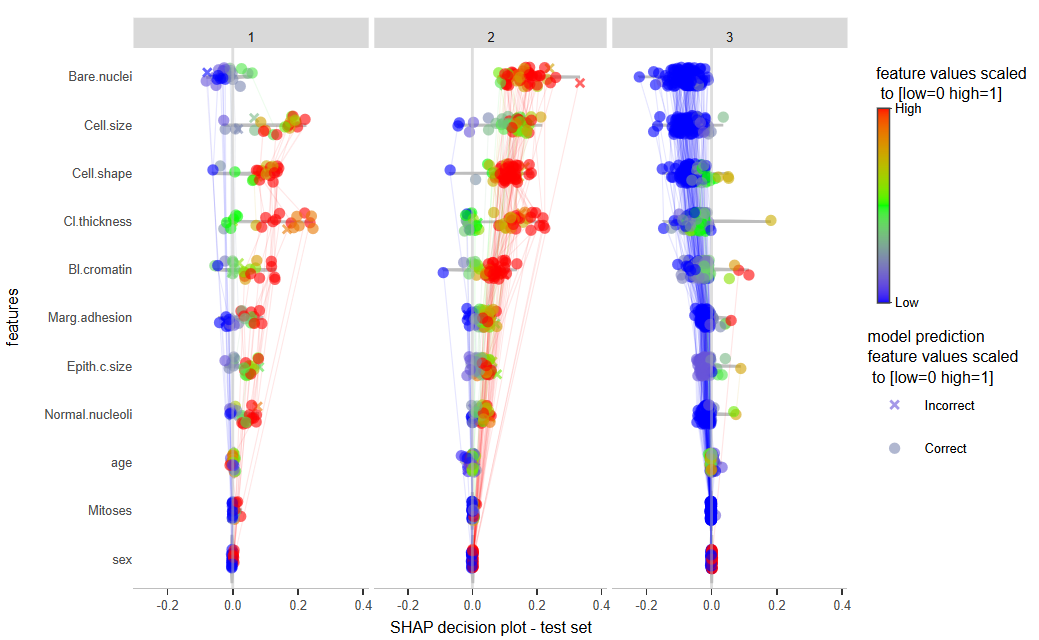
▲ 可以看到,三种聚类的解释性是不一样的。
展示不同聚类亚型的混淆矩阵:
# 显示与 SHAP 亚型(由 SHAP 聚类确定的患者子集)对应的混淆矩阵
SHAP_plot_clusters[[2]]
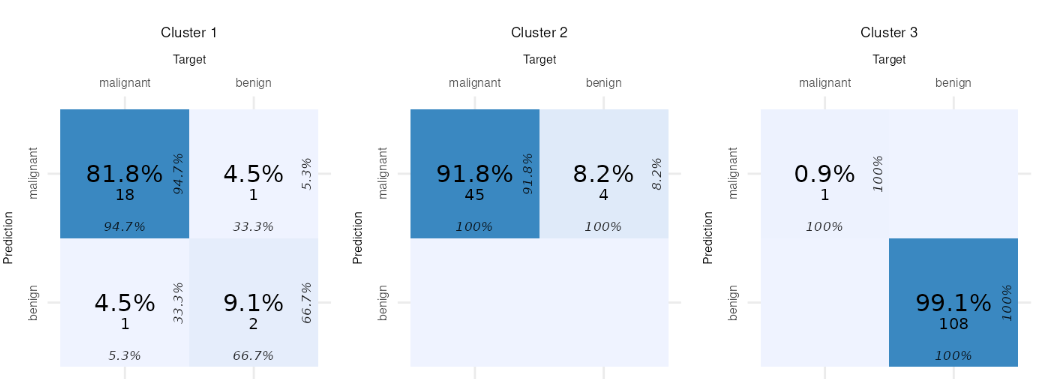
▲ 如上,模型在不同的患者亚型的表现是不一样的,说明他们在特征上存在一定差别。
⑧ 模型公平性(敏感性分析)。对于不同子组,如性别,我们有时想研究模型的表现是否公平(在不同性别的人群中表现是一致的)。
Fairness_results <- eFairness(task = maintask,
trained_model = mylrn,
splits = splits,
target_variable = "sex",
var_levels = c("Male", "Female"))
# 训练集(左)和测试集(右)不同子分组的 ROC 曲线
Fairness_results[[1]]
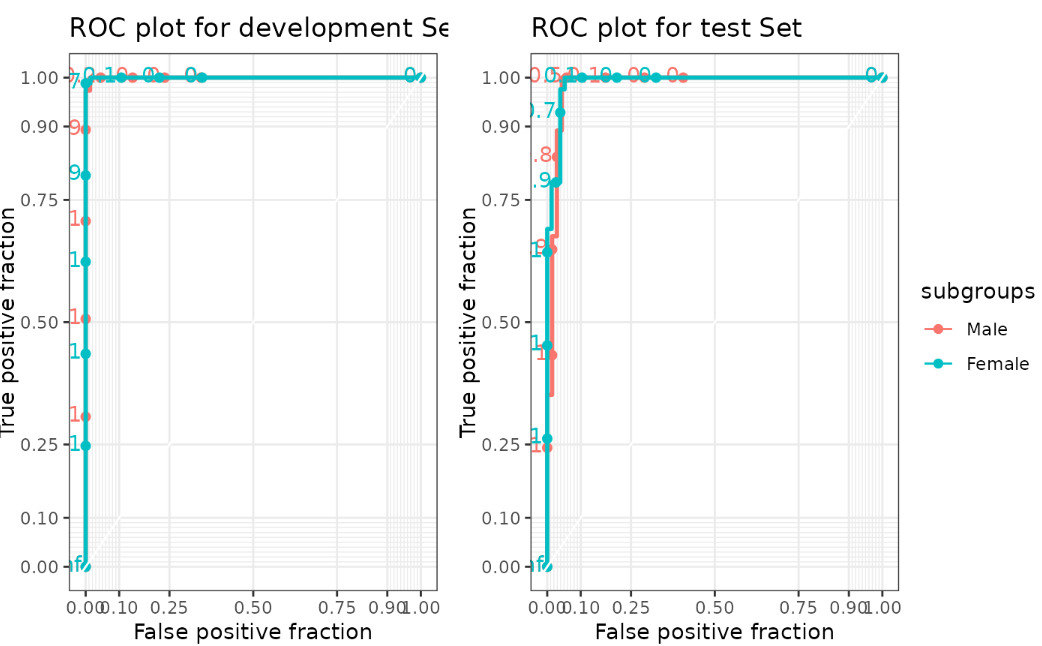
⑨ 最后,可以看看模型的参数:
# get model parameters
model_params <- mylrn$param_set
print(data.table::as.data.table(model_params))
## id class lower upper
## <char> <char> <num> <num>
## 1: alpha ParamDbl -Inf Inf
## 2: always.split.variables ParamUty NA NA
## 3: class.weights ParamUty NA NA
## 4: holdout ParamLgl NA NA
## 5: importance ParamFct NA NA
## 6: keep.inbag ParamLgl NA NA
## 7: max.depth ParamInt 0 Inf
## 8: min.bucket ParamInt 1 Inf
## 9: min.node.size ParamInt 1 Inf
## 10: minprop ParamDbl -Inf Inf
## 11: mtry ParamInt 1 Inf
## 12: mtry.ratio ParamDbl 0 1
## 13: num.random.splits ParamInt 1 Inf
## 14: node.stats ParamLgl NA NA
## 15: num.threads ParamInt 1 Inf
## 16: num.trees ParamInt 1 Inf
## 17: oob.error ParamLgl NA NA
## 18: regularization.factor ParamUty NA NA
## 19: regularization.usedepth ParamLgl NA NA
## 20: replace ParamLgl NA NA
## 21: respect.unordered.factors ParamFct NA NA
## 22: sample.fraction ParamDbl 0 1
## 23: save.memory ParamLgl NA NA
## 24: scale.permutation.importance ParamLgl NA NA
## 25: se.method ParamFct NA NA
## 26: seed ParamInt -Inf Inf
## 27: split.select.weights ParamUty NA NA
## 28: splitrule ParamFct NA NA
## 29: verbose ParamLgl NA NA
## 30: write.forest ParamLgl NA NA
## id class lower upper
## levels nlevels is_bounded
## <list> <num> <lgcl>
## 1: [NULL] Inf FALSE
## 2: [NULL] Inf FALSE
## 3: [NULL] Inf FALSE
## 4: TRUE,FALSE 2 TRUE
## 5: none,impurity,impurity_corrected,permutation 4 TRUE
## 6: TRUE,FALSE 2 TRUE
## 7: [NULL] Inf FALSE
## 8: [NULL] Inf FALSE
## 9: [NULL] Inf FALSE
## 10: [NULL] Inf FALSE
## 11: [NULL] Inf FALSE
## 12: [NULL] Inf TRUE
## 13: [NULL] Inf FALSE
## 14: TRUE,FALSE 2 TRUE
## 15: [NULL] Inf FALSE
## 16: [NULL] Inf FALSE
## 17: TRUE,FALSE 2 TRUE
## 18: [NULL] Inf FALSE
## 19: TRUE,FALSE 2 TRUE
## 20: TRUE,FALSE 2 TRUE
## 21: ignore,order,partition 3 TRUE
## 22: [NULL] Inf TRUE
## 23: TRUE,FALSE 2 TRUE
## 24: TRUE,FALSE 2 TRUE
## 25: jack,infjack 2 TRUE
## 26: [NULL] Inf FALSE
## 27: [NULL] Inf FALSE
## 28: gini,extratrees,hellinger 3 TRUE
## 29: TRUE,FALSE 2 TRUE
## 30: TRUE,FALSE 2 TRUE
## levels nlevels is_bounded
## special_vals default storage_type tags
## <list> <list> <char> <list>
## 1: <list[0]> 0.5 numeric train
## 2: <list[0]> <NoDefault[0]> list train
## 3: <list[0]> [NULL] list train
## 4: <list[0]> FALSE logical train
## 5: <list[0]> <NoDefault[0]> character train
## 6: <list[0]> FALSE logical train
## 7: <list[1]> [NULL] integer train
## 8: <list[0]> 1 integer train
## 9: <list[1]> [NULL] integer train
## 10: <list[0]> 0.1 numeric train
## 11: <list[1]> <NoDefault[0]> integer train
## 12: <list[0]> <NoDefault[0]> numeric train
## 13: <list[0]> 1 integer train
## 14: <list[0]> FALSE logical train
## 15: <list[0]> 1 integer train,predict,threads
## 16: <list[0]> 500 integer train,predict,hotstart
## 17: <list[0]> TRUE logical train
## 18: <list[0]> 1 list train
## 19: <list[0]> FALSE logical train
## 20: <list[0]> TRUE logical train
## 21: <list[0]> ignore character train
## 22: <list[0]> <NoDefault[0]> numeric train
## 23: <list[0]> FALSE logical train
## 24: <list[0]> FALSE logical train
## 25: <list[0]> infjack character predict
## 26: <list[1]> [NULL] integer train,predict
## 27: <list[0]> [NULL] list train
## 28: <list[0]> gini character train
## 29: <list[0]> TRUE logical train,predict
## 30: <list[0]> TRUE logical train
## special_vals default storage_type tags
简单分享到这里
欢迎各位佬哥关注
匿了
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容








所有评论(0)