本文以感知器为例，介绍了从零实现机器学习方法的具体步骤以及重要性。

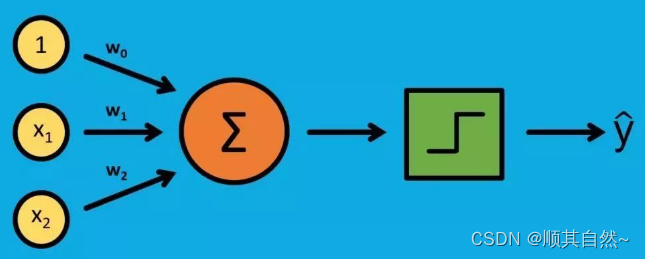
从头开始写机器学习算法能够获得很多经验。当你最终完成时，你会惊喜万分，而且你明白这背后究竟发生了什么。

有些算法比较复杂，我们不从简单的算法开始，而是要从非常简单的算法开始，比如单层感知器。

本文以感知器为例，通过以下 6 个步骤引导你从头开始写算法：

1）对算法有基本的了解

2）找到不同的学习资源

3）将算法分解成块

4）从简单的例子开始

5）用可信的实现进行验证

6）写下你的过程

01、基本了解

不了解基础知识，就无法从头开始处理算法。至少，你要能回答下列问题：

1）它是什么?

2）它一般用在什么地方?

3）什么时候不能用它?

就感知器而言，这些问题的答案如下：

1）单层感知器是最基础的神经网络，一般用于二分类问题(1 或 0，「是」或「否」)。

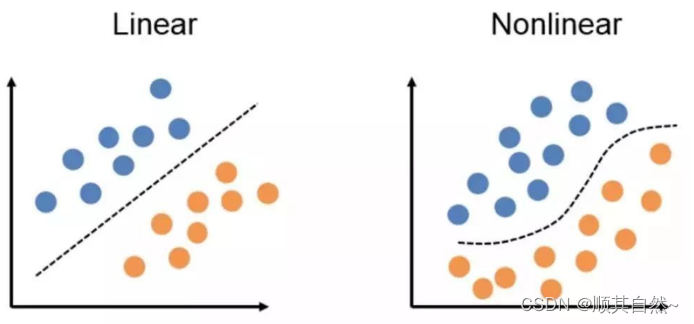
2）它可以应用在一些简单的地方，比如情感分析(积极反应或消极反应)、贷款违约预测(「会违约」，「不会违约」)。在这两种情况中，决策边界都是线性的。

3）当决策边界是非线性的时候不能使用感知器，要用不同的方法。

02、借助不同的学习资源

在对模型有了基本了解之后，就可以开始研究了。有人用教科书学得更好，而有人用视频学得更好。就我而言，我喜欢到处转转，用各种各样的资源学习。

如果是学数学细节的话，书的效果很好，但对于更实际的例子，我更推荐博客和 YouTube 视频。大家可以根据自己需求，进行选择。

03、将算法分解成块

现在我们已经收集好了资料，是时候开始学习了。与其从头读一个章节或者一篇博客，不如先浏览章节标题和其他重要信息。写下要点，并试着概述算法。

在看过这些资料之后，我将感知器分成下列 5 个模块：

1）初始化权重（机器学习的目标就是找到各自变量合适的权重值）

2）将输入和权重相乘之后再求和

3）比较上述结果和阈值，计算输出(1 或 0)（输入激活函数，输出预测值）

4）更新权重（使预测值接近实际值）

5）重复

接下来我们详细叙述每一个模块的内容。

1、初始化权重

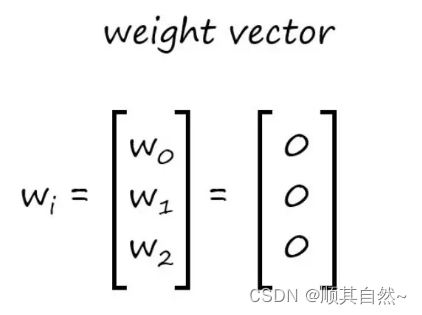
首先，我们要初始化权重向量。

权重数量要和特征数量相同。假设我们有三个特征，权重向量如下图所示。权重向量一般会初始化为 0，此例中将一直采用该初始化值。

2、输入和权重相乘再求和

接下来，我们就要将输入和权重相乘，再对其求和。为了更易于理解，我给第一行中的权重及其对应特征涂上了颜色。

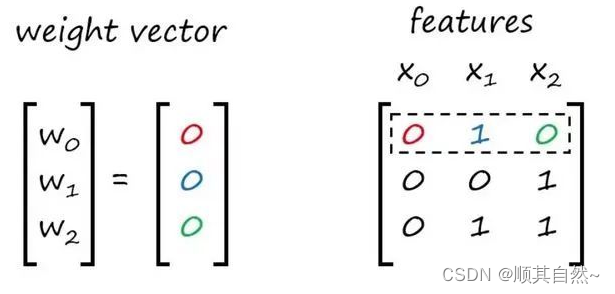
在我们将特征和权重相乘之后，对乘积求和。一般将其称为点积。

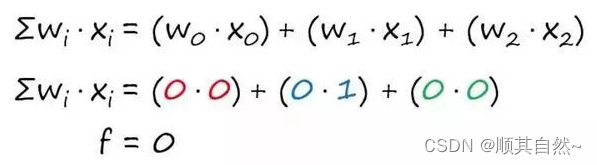
最终结果是 0，此时用「f」表示这个暂时的结果。（只是加权加和的结果，还没有和阈值比较，判断是否可以激活，所以并不是最终输出结果）

3、和阈值比较（激活函数）

计算出点积后，我们要将它和阈值进行比较。我将阈值定为 0，你可以用这个阈值，也可以试一下其他值。（下面这个函数就是激活函数，只有超过阈值，才算激活）（激活可以理解为打开开关，用手按开关，按到一定力度之后，开关才会打开，灯才会亮）

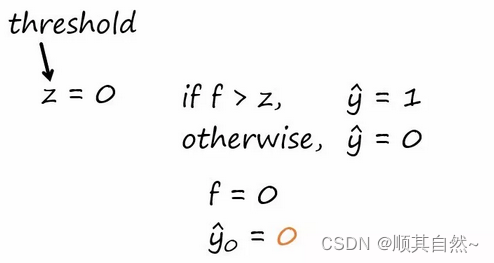
由于之前计算出的点积「f」为 0，不比阈值 0 大，因此估计值也等于 0。

将估计值标记为「y hat」，y hat 的下标 0 对应的是第一行。当然你也可以用 1 表示第一行，这无关紧要，我选择从 0 开始。

如果将这个结果和真值比较的话，可以看出我们当前的权重没有正确地预测出真实的输出。

注：

y hat表示预测值。

y^，就念做y hat，用来表示预测值，估计值的，当然你要是读作y尖，y帽也可以的，正式中文名一般是读的是y的估计值或者y的预测值。

预测值是按一定的数字模型并根据历史资料推算出来的，它不可能与未来的实际情况完全相符，预测值只是对未来情况的估计值，具有定的假定性和近似性。

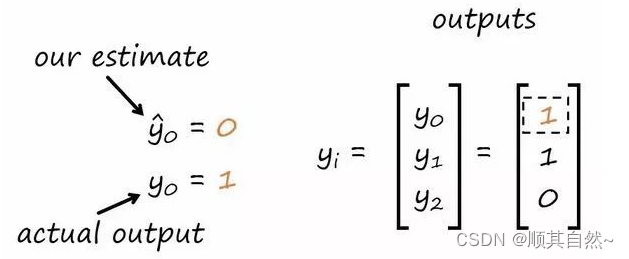
由于我们的预测错了，因此要更新权重，这就要进行下一步了。

4、更新权重

我们要用到下面的等式：

基本思想是在迭代「n」时调整当前权重，这样我们将在下一次迭代「n+1」时得到新权重。

为了调整权重，我们需要设定「学习率」，用希腊字母「eta(η)」标记。我将学习率设为 0.1，当然就像阈值一样，你也可以用不同的数值。

机器学习中的 w[j] = w[j] + eta * (y[i] - yhat) * x[i][j] 表示的是在梯度下降算法中权重更新的过程。

具体来说，这个公式是梯度下降法中的一个关键步骤，用于更新模型参数（权重）以最小化损失函数。在这个公式中：

w[j] 表示当前第 j 个特征的权重。

eta 是学习率，它控制着我们在梯度下降过程中每一步走多远。学习率是一个超参数，需要根据问题的特性来设定。

(y[i] - yhat) 表示的是预测值与真实值之间的误差，其中 y[i] 是样本的真实标签，而 yhat 是模型对第 i 个样本的预测标签。

x[i][j] 表示第 i 个样本的第 j 个特征的值。

在每次迭代中，模型会根据这个公式调整每个特征对应的权重，以便减少预测值和真实值之间的差距。通过多次迭代，模型的权重将逐渐收敛到最优解，即损失函数取得最小值时的权重值。这个过程是机器学习中常用的一种优化技术，用于训练模型并提高其预测性能。

总结来说，这个公式体现了机器学习中通过梯度下降法进行权重更新的过程，目的是通过不断调整权重来最小化损失函数，从而提高模型的预测准确性。

在机器学习的梯度下降法中，权重更新公式中的 x[i][j] 乘法项是至关重要的。这一步骤反映了特征j在样本i上的贡献对于权重调整的影响程度。

首先，x[i][j]代表的是第i个训练样本的第j个特征值。在机器学习中，模型对每个输入样本做出预测，并根据预测结果与真实标签之间的误差来更新模型参数，即权重。这个误差通常是通过损失函数来计算的，而在梯度下降法中，我们会计算损失函数关于每个权重的梯度，以确定如何调整权重以减小损失。

其次，乘以x[i][j]实际上是在计算偏导数的过程中，将误差传递回每个特征。这样，就可以根据每个特征对预测误差的贡献程度来相应地调整其权重。如果某个特征的值较大，那么它对预测误差的贡献也大，相应地，该特征的权重调整幅度也会更大。反之，如果特征值较小，则对该特征的权重调整幅度也会较小。

最后，这种权重调整方式有助于模型学习到不同特征的重要性，从而在未来的预测中更好地泛化到新的数据上。这是基于模型对损失函数进行优化的核心机制，通过不断地调整权重来最小化损失函数，从而使模型的预测结果尽可能接近真实值。

综上所述，乘以x[i][j]是为了确保每个特征根据其对模型预测误差的贡献程度来调整权重，这是梯度下降法中权重更新的关键步骤。

目前本教程主要介绍了：

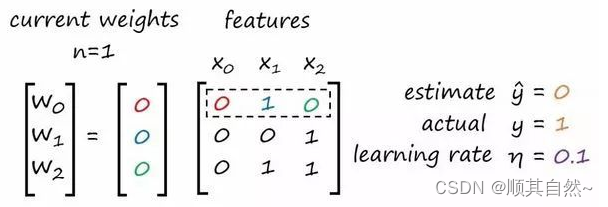
现在我们要继续计算迭代 n=2 时的新权重了。

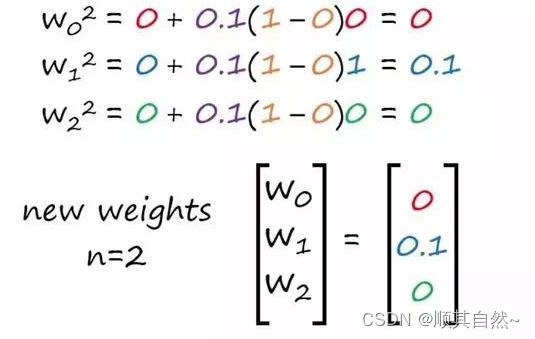
我们成功完成了感知器算法的第一次迭代。

5、重复

由于我们的算法没能计算出正确的输出，因此还要继续。

一般需要进行大量的迭代。遍历数据集中的每一行，每一次迭代都要更新权重。一般将完整遍历一次数据集称为一个「epoch」。（epoch：时期； 纪元；世；新时代）

我们的数据集有 3 行，因此如果要完成 1 个 epoch 需要经历 3 次迭代。我们也可以设置迭代总数或 epoch 数来执行算法，比如指定 30 次迭代(或 10 个 epoch)。与阈值和学习率一样，epoch 也是可以随意使用的参数。

在下一次迭代中，我们将使用第二行特征。

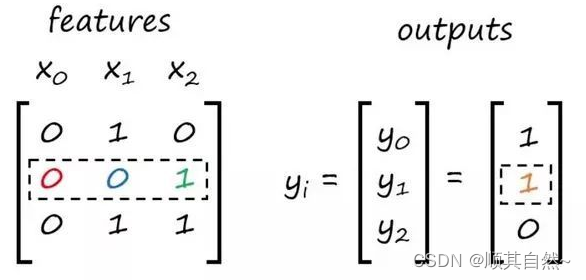
此处不再重复计算过程，下图给出了下一个点积的计算：

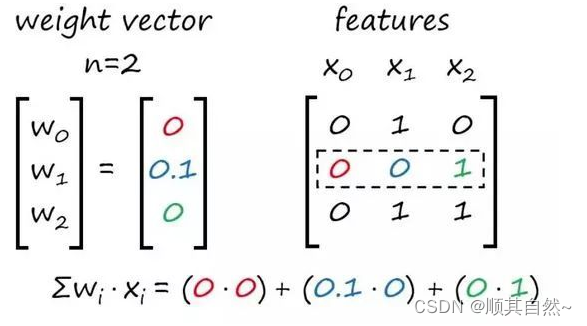
接着就可以比较该点积和阈值来计算新的估计值、更新权重，然后再继续。如果我们的数据是线性可分的，那么感知器最终将会收敛。

04、从简单的例子开始

我们已经将算法分解成块了，接下来就可以开始用代码实现它了。

简单起见，我一般会以非常小的「玩具数据集」开始。对这类问题而言，有一个很好的小型线性可分数据集，它就是与非门(NAND gate)。这是数字电路中一种常见的逻辑门。

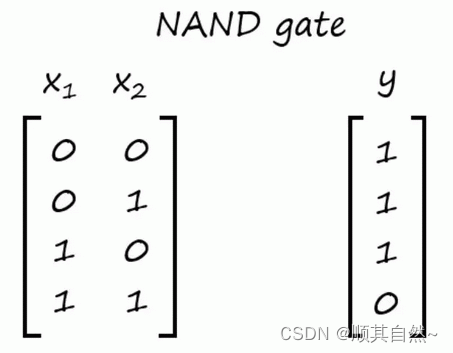
由于这个数据集很小，我们可以手动将其输入到 Python 中。我添加了一列值为 1 的虚拟特征(dummy feature)「x0」，这样模型就可以计算偏置项了（有了偏置后才可以保证分类线不穿过原点）。你可以将偏置项视为可以促使模型正确分类的截距项。

以下是输入数据的代码：

# Importing libraries
# NAND Gate
# Note: x0 is a dummy variable for the bias term
# x0 x1 x2
x = [[1., 0., 0.],
[1., 0., 1.],
[1., 1., 0.],
[1., 1., 1.]]
y =[1.,
1.,
1.,
0.]

与前面的章节一样，我将逐步完成算法、编写代码并对其进行测试。

1. 初始化权重

第一步是初始化权重。

# Initialize the weights
import numpy as np
w = np.zeros(len(x[0]))

Out:

[ 0. 0. 0.]

注意权重向量的长度要和特征长度相匹配。以 NAND 门为例，它的长度是 3。

2、将权重和输入相乘并对其求和

我们可以用 Numpy 轻松执行该运算，要用的方法是 .dot()。

从权重向量和第一行特征的点积开始。

# Dot Product
f = np.dot(w, x[0])
print f

Out:

0.0

如我们所料，结果是 0。为了与前面的笔记保持连贯性，设点积为变量「f」。

3、与阈值相比较

为了与前文保持连贯，将阈值「z」设为 0。若点积「f」大于 0，则预测值为 1，否则，预测值为 0。将预测值设为变量 yhat。

# Activation Function  激活函数
z = 0.0
if f > z:
    yhat = 1.
else:
    yhat = 0.
print yhat

Out:

0.0

正如我们所料，预测值是 0。

你可能注意到了在上文代码的注释中，这一步被称为「激活函数」。这是对这部分内容的更正式的描述。

从 NAND 输出的第一行可以看到实际值是 1。由于预测值是错的，因此需要继续更新权重。

4. 更新权重

现在已经做出了预测，我们准备更新权重。

# Update the weights
eta = 0.1
w[0] = w[0] + eta*(y[0] - yhat)*x[0][0]
w[1] = w[1] + eta*(y[0] - yhat)*x[0][1]
w[2] = w[2] + eta*(y[0] - yhat)*x[0][2]
print w

Out:

[ 0.1 0. 0. ]

要像前文那样设置学习率。为与前文保持一致，将学习率 η 的值设为 0.1。为了便于阅读，我将对每次权重的更新进行硬编码。

权重更新完成。

5、重复

现在我们完成了每一个步骤，接下来就可以把它们组合在一起了。

我们尚未讨论的最后一步是损失函数，我们需要将其最小化，它在本例中是误差项平方和。（损失越小越好）

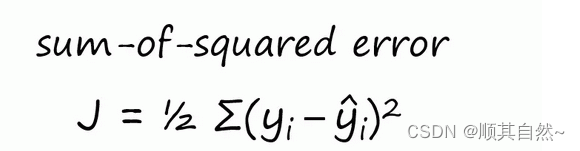
我们要用它来计算误差，然后看模型的性能。

把它们都放在一起，就是完整的函数：

import numpy as np
# Perceptron function  感知机函数
def perceptron(x, y, z, eta, t):
    '''
    Input Parameters:
        x: data set of input features 输入特征数据集
        y: actual outputs  实际输出
        z: activation function threshold  激活函数阈值
        eta: learning rate  学习率
        t: number of iterations  迭代次数
    '''

    # initializing the weights  初始化权重
    w = np.zeros(len(x[0]))      
    n = 0                        

    # initializing additional parameters to compute sum-of-squared errors
    yhat_vec = np.ones(len(y))     # vector for predictions 预测向量
    errors = np.ones(len(y))       # vector for errors (actual - predictions) 误差向量（实际-预测）
    J = []                         # vector for the SSE cost function 平方和误差SSE损失函数向量

    while n < t:
        for i in range(0, len(x)):
            # dot product  向量点乘
            f = np.dot(x[i], w)
            # activation function  激活函数
            if f >= z:
                yhat = 1.
            else:                                   
                yhat = 0.
            yhat_vec[i] = yhat

            # updating the weights  更新权重
            # 通过不断调整权重，当y[i]=yhat时，权重就不再改变了，只要不相等，就继续学
            for j in range(0, len(w)):
                w[j] = w[j] + eta * (y[i]-yhat) * x[i][j]

        n += 1
        # computing the sum-of-squared errors 计算平方和(SSE)误差
        for i in range(0,len(y)):
           errors[i] = (y[i] - yhat_vec[i])**2
        J.append(0.5 * np.sum(errors))

    return w, J

现在已经编写了完整的感知器代码，接着是运行代码：

#     x0  x1  x2
x = [[1., 0., 0.],
     [1., 0., 1.],
     [1., 1., 0.],
     [1., 1., 1.]]

y =[1.,
    1.,
    1.,
    0.]

z = 0.0
eta = 0.1
t = 50

print("The weights are:")
print(perceptron(x, y, z, eta, t)[0])

print("The errors are:")
print(perceptron(x, y, z, eta, t)[1])

The weights are:
[ 0.2 -0.2 -0.1]
The errors are:
[0.5, 1.5, 1.5, 1.0, 0.5, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

我们可以看到，第 6 次迭代时误差趋近于 0，且在剩余迭代中误差一直是 0。当误差趋近于 0 并保持为 0 时，模型就收敛了。这告诉我们模型已经正确「学习」了适当的权重。

下一部分，我们将用计算好的权重在更大的数据集上进行预测。

05、用可信的实现进行验证

到目前为止，我们已经找到了不同的学习资源、手动完成了算法，并用简单的例子测试了算法。

我们将按照以下几步进行比较：

1）导入数据

2）将数据分割为训练集和测试集

3）训练感知器

4）测试感知器

5）和 scikit-learn 感知器进行比较

1、导入数据

首先导入数据。你可以在这里

(https://github.com/dataoptimal/posts/blob/master/algorithms from scratch/dataset.csv)得到数据集的副本。这是我创建的线性可分数据集，确保感知器可以起作用。为了确认，我们还将数据绘制成图。

注：github上的链接已经失效，可以通过如下方式生成测试数据集

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# Example1: make_classification()生成二分类数据集
from sklearn.datasets import make_classification

X, y = make_classification(n_samples=1000, n_features=5, n_redundant=0, n_clusters_per_class=1, n_informative=1,
                           n_classes=2, random_state=20)

# scatter plot, dots colored by class value
df = pd.DataFrame(dict(z=1, x=X[:, 0], y=X[:, 1], label=y))
df.to_csv('dataset.csv', index=None)

从图中很容易看出来，我们可以用一条直线将数据分开。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv("dataset.csv")
plt.scatter(df.values[:,1], df.values[:,2], c = df['label'], alpha=0.8)
plt.show()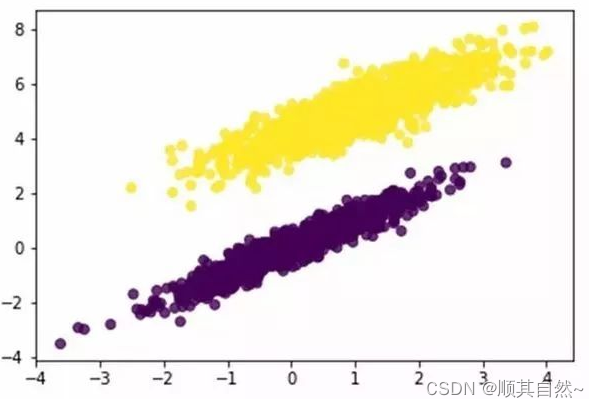

在继续之前，我先解释一下绘图的代码。我用 Pandas 导入 csv，它可以自动将数据放入 DataFrame 中。为了绘制数据，我要将值从 DataFrame 中取出来，因此我用了 .values 方法。特征在第一列和第二列，因此我在散点图函数中用了这些特征。第 0 列是值为 1 的虚拟特征，这样就能计算截距。这与上一节中的 NAND 门操作相似。最后，在散点图函数中令c = df['3'], alpha = 0.8 为两个类着色。输出是第三列数据(0 或 1)，所以我告诉函数用列「3」给这两个类着色。

你可以在此处

(https://matplotlib.org/api/_as_gen/matplotlib.pyplot.scatter.html)找到更多关于 Matplotlib 散点图函数的信息。

2、将数据分割成训练集 / 测试集

现在我们已经确定数据可线性分割，那么是时候分割数据了。

在与测试集不同的数据集上训练模型是很好的做法，这有助于避免过拟合。还有不同的方法，但是简单起见，我要用一个训练集和一个测试集。首先打乱数据。

df = df.values
np.random.seed(5)
np.random.shuffle(df)

先将数据从 DataFrame 变为 numpy 数组。这样就可以更容易地使用 numpy 函数了，比如 .shuffle。为了结果的可重复性，我设置了随机种子 (5)。完成后，我试着改变随机种子，并观察结果会产生怎样的变化。接下来，我将 70% 的数据分为训练集，将 30% 的数据作为测试集。

train = df[0:int(0.7*len(df))]
test = df[int(0.7*len(df)):int(len(df))]

最后一步是分离训练集和测试集的特征和输出。

x_train = train[:, 0:3]
y_train = train[:, 3]
x_test = test[:, 0:3]
y_test = test[:, 3]

我在这个例子中将 70% 的数据作为训练集，将 30% 的数据作为测试集，你们可以研究 k 折交叉验证等其他方法。

3、训练感知器

我们可以重复使用之前的章节中构建的代码。

def perceptron_train(x, y, z, eta, t):
    '''  Input Parameters:
        x: data set of input features
        y: actual outputs
        z: activation function threshold
        eta: learning rate
        t: number of iterations
    '''
    # initializing the weights
    w = np.zeros(len(x[0]))      
    n = 0                        
    # initializing additional parameters to compute sum-of-squared errors
    yhat_vec = np.ones(len(y))     # vector for predictions
    errors = np.ones(len(y))       # vector for errors (actual - predictions)
    J = []                         # vector for the SSE cost function

    while n < t:
        for i in range(0, len(x)):
            # dot product             
            f = np.dot(x[i], w)                                   
            # activation function             
            if f >= z:                               
                yhat = 1.                               
            else:                                   
                yhat = 0.
            yhat_vec[i] = yhat

            # updating the weights
            for j in range(0, len(w)):             
                w[j] = w[j] + eta*(y[i]-yhat)*x[i][j]

        n += 1
        # computing the sum-of-squared errors
        for i in range(0,len(y)):     
           errors[i] = (y[i]-yhat_vec[i])**2
        J.append(0.5*np.sum(errors))
    return w, J
z = 0.0
eta = 0.1
t = 50
perceptron_train(x_train, y_train, z, eta, t)

接下来看权重和误差项平方和。

w = perceptron_train(x_train, y_train, z, eta, t)[0]
J = perceptron_train(x_train, y_train, z, eta, t)[1]
print(w)
print(J)
Out:
[-0.5        -0.29850122  0.35054929]
[4.5, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

现在权重对我们来说意义不大了，但是我们在测试感知器时还要再使用这些数值，以及用这些权重比较我们的模型和 scikit-learn 的模型。

根据误差项平方和可以看出，感知器已经收敛了，这是我们预料中的结果，因为数据是线性可分的。

4、测试感知器

现在是时候测试感知器了。我们要建立一个小的 perceptron_test 函数来测试模型。与前文类似，这个函数取我们之前用 perceptron_train 函数和特征计算出的权重的点积以及激活函数进行预测。之前唯一没见过的只有 accuracy_score，这是 scikit-learn 中的评估指标函数。

将所有的这些放在一起，代码如下：

from sklearn.metrics import accuracy_score
w = perceptron_train(x_train, y_train, z, eta, t)[0]
def perceptron_test(x, w, z, eta, t):
    y_pred = []
    for i in range(0, len(x-1)):
        f = np.dot(x[i], w)   
        # activation function
        if f > z:                               
            yhat = 1                               
        else:                                   
            yhat = 0
        y_pred.append(yhat)
    return y_pred

y_pred = perceptron_test(x_test, w, z, eta, t)

print("The accuracy score is:")
print(accuracy_score(y_test, y_pred))

Out:
The accuracy score is:
1.0

得分为 1.0 表示我们的模型在所有的测试数据上都做出了正确的预测。因为数据集明显是可分的，所以结果正如我们所料。

5、和 scikit-learn 感知器进行比较

最后一步是将我们的感知器和 scikit-learn 的感知器进行比较。下面的代码是 scikit-learn 感知器的代码：

from sklearn.linear_model import Perceptron
# training the sklearn Perceptron
clf = Perceptron(random_state=None, eta0=0.1, shuffle=False, fit_intercept=False)
clf.fit(x_train, y_train)
clf.predict(x_test)
print(clf.coef_)

现在我们已经训练了模型，接下来要比较这个模型的权重和我们的模型计算出来的权重。

Out:

sklearn weights:

[-0.5 -0.29850122 0.35054929]

my perceptron weights:

[-0.5 -0.29850122 0.35054929]

scikit-learn 模型中的权重和我们模型的权重完全相同。这意味着我们的模型可以正确地工作，这是个好消息。

在结束之前还有一些小问题。在 scikit-learn 模型中，我们将随机状态设置为「None」而且没有打乱数据。这是因为我们已经设置了随机种子，而且已经打乱过数据，不用再做一次。还需要将学习率 eta0 设置为 0.1，和我们的模型相同。最后一点是截距。因为我们已经设置了值为 1 的虚拟特征列，因此模型可以自动拟合截距，所以不必在 scikit-learn 感知器中打开它。

这些看似都是小细节，但是如果不设置它们的话，我们的模型就无法重复得到相同的结果。这是重点。在使用模型之前，阅读文档并了解不同的设置有什么作用非常重要。

06、写下你的过程

这是该过程的最后一步，可能也是最重要的一步。

你刚刚经历了学习、做笔记、从头开始写算法以及用可信实现进行比较的流程。不要浪费这些努力!

写下过程原因有二：

你要更深刻地理解这个过程，因为你还要将你学到的东西教给别人。

你要向潜在雇主展示这个过程。

从机器学习库中实现算法是一回事，从头开始实现算法是另一回事，它会给人留下深刻印象。

GitHub 个人资料是展示你所做工作的一种很好的方法。

总结

本文介绍了如何从零开始实现感知器。这是一种在更深层次上学习算法的好方法，而你还可以自己实现它。你在大多数情况下用的都是可信的实现，但是如果你真的想要更深入地了解背后发生了什么，从头实现算法是很好的练习。

转自：6个步骤从头开始编写机器学习算法：感知器案例研究 - 知乎

# 算法 # 机器学习 # 人工智能
Logo
EazyDevelop社区

一站式 AI 云服务平台

更多推荐

cover

5分钟搞定！MySQL/PostgreSQL 到 Elasticsearch 的实时同步

avatar EazyDevelop社区
cover

两小时，我搭了一套销售提成计算系统

avatar EazyDevelop社区
cover

零代码时代：如何利用聚合API平台快速构建你的专属AI Agent

avatar EazyDevelop社区