特征融合方法

1. 合并通道（Channel Concatenation）

通过将多个通道的特征图拼接在一起，形成一个更高维度的特征表示。这种方法通常用于多模态数据或多尺度特征的融合，在视觉任务中，常见于多通道卷积神经网络中。

2. 加法融合（Additive Fusion）

通过对不同特征图进行逐元素加法操作，生成一个新的融合特征。这种方法假设多个特征之间有一定的互补性，通过加法操作将它们融合为一个更为丰富的表示。

为何加法融合后的特征不会消失？

在加法融合过程中，得到的新特征是原始特征的某种组合。假设有两个特征图 A 和 B 加法融合后的特征图 C 为：

$$C=A+B$$

1. 可逆性和信息保留：

在加法融合的过程中，理论上，融合后的特征图 C 仍然能够包含 A 和 B 的信息。如果融合过程是线性的且没有额外的操作（如丢弃或压缩），比如A, B特征的位置不同，相加后互不影响，则可以通过简单的逆操作将融合前的特征图恢复出来。因此，从数学上讲，加法融合是信息保留的，特征不会完全丢失。这种简单情况我们不再赘述。

2. 信号处理中的类比

在加法融合后，尽管在时域上可能发生了某些干扰或叠加，原始特征的信息依然存在于频域中。例如，通过对特征图进行傅里叶变换（Fourier Transform），可以将时域中的加法操作转化为频域中的不同频率成分的叠加。傅里叶变换能够解耦各个频率成分，从而恢复出原始特征的频率信息。通过频域分析，我们仍然可以提取出与原始特征相关的高频或低频分量。

关于傅里叶变换

傅里叶级数

傅里叶级数是用来表示周期函数的数学工具。它通过将函数分解为正弦和余弦函数的无穷级数来实现。这种方法在信号处理、振动分析、声学、电气工程等领域有广泛应用。

1. 正弦和余弦函数：
   • 傅里叶级数使用这些函数作为基函数，因为它们是周期性的。
2. 傅里叶级数形式：
   • 对于一个周期为 T 的函数 f(x) ，其傅里叶级数表示为：
     $$f(x)=a_0+\sum _{n=1}^{\infty }\left(a_n\cos \left(\frac{2\pi nx}{T}\right)+b_n\sin \left(\frac{2\pi nx}{T}\right)\right)$$
     $a_0$、$a_n$、$b_n$ 是傅里叶系数，表示函数在相应频率上的幅度。
3. 傅里叶系数的计算：
   通过积分计算得到：
   $$a_0=\frac{1}{T}{\int }_0^{T}f(x)dx$$
   $$a_n=\frac{2}{T}{\int }_0^{T}f(x)\cos \left(\frac{2\pi nx}{T}\right)dx$$
   $$b_n=\frac{2}{T}{\int }_0^{T}f(x)\sin \left(\frac{2\pi nx}{T}\right)dx$$

傅里叶级数中的系数n

通常情况下，当傅里叶级数的系数对应的频率 𝑛 增加时，对函数的拟合效果会逐渐递减，尤其是对于平滑的周期函数。这是因为高频的傅里叶分量对应着更小的波动，它们对函数的主要形态贡献较小。所以，当我们需要进行拟合时，只需要前k（本人一般取3）项，就可以得到基本形状。让我们分析一下这个现象：

1. 傅里叶级数与拟合效果

傅里叶级数是将一个周期函数分解为不同频率的正弦波和余弦波的和。形式上，对于一个周期为 𝑇的函数 f(x)，其中，$a_n$和$b_n$是傅里叶系数。高频成分（即大n）对应于函数的快速变化，低频成分（即小n）则对应于函数的大致趋势或主要变换。

2. 低频分量和高频分量的作用

• 低频分量（小n）：这些分量描述了函数的基本形态、平滑趋势，通常能捕捉到大部分函数的变化。例如$a_1\cos (x)$, $b_1\sin (x)$等低频项对函数的主要趋势影响很大。
• 高频分量（大n）：随着n增大，这些频率对应的波形变得越来越快，主要描述的是函数的小幅变化和高频振荡。因此，这些高频项对拟合效果的贡献逐渐减小。

傅里叶拟合实验

简单示例

给定周期函数 f(x)，定义如下：

$$f(x)=\{\begin{array}{ll}1,& 0\le x<\pi \\ -1,& \pi \le x<2\pi \end{array}$$

并且 $f(x+2\pi )=f(x)$ 对所有 x 成立。

好的，我们来计算这些傅里叶系数。

1) 计算 $a_0$

$a_0$ 是函数在一个周期内的平均值：

$$a_0=\frac{1}{2\pi }{\int }_0^{2\pi }f(x)dx$$

将 f(x) 的定义代入：

$$a_0=\frac{1}{2\pi }\left({\int }_0^{\pi }1dx+{\int }_{\pi }^{2\pi }(-1)dx\right)$$

计算积分：

$$a_0=\frac{1}{2\pi }\left([x{]}_0^{\pi }-[x{]}_{\pi }^{2\pi }\right)=\frac{1}{2\pi }(\pi -\pi )=0$$

2) 计算 $a_n$

$a_n$ 是余弦项的系数：

$$a_n=\frac{1}{\pi }{\int }_0^{2\pi }f(x)\cos (nx)dx$$

将 f(x) 的定义代入：

$$a_n=\frac{1}{\pi }\left({\int }_0^{\pi }\cos (nx)dx+{\int }_{\pi }^{2\pi }(-\cos (nx))dx\right)$$

计算这两个积分：

$$a_n=\frac{1}{\pi }\left({\left[\frac{\sin (nx)}{n}\right]}_0^{\pi }-{\left[\frac{\sin (nx)}{n}\right]}_{\pi }^{2\pi }\right)$$

由于 $\sin (n\pi )=0$ ，所以：

$$a_n=0$$

3) 计算 $b_n$

$b_n$是正弦项的系数：

$$b_n=\frac{1}{\pi }{\int }_0^{2\pi }f(x)\sin (nx)dx$$

将 f(x) 的定义代入：

$$b_n=\frac{1}{\pi }\left({\int }_0^{\pi }\sin (nx)dx+{\int }_{\pi }^{2\pi }(-\sin (nx))dx\right)$$

计算这两个积分：

$$b_n=\frac{1}{\pi }\left({\left[-\frac{\cos (nx)}{n}\right]}_0^{\pi }+{\left[\frac{\cos (nx)}{n}\right]}_{\pi }^{2\pi }\right)$$

计算结果：

$$b_n=\frac{1}{\pi }\left(-\frac{\cos (n\pi )-1}{n}+\frac{\cos (2n\pi )-\cos (n\pi )}{n}\right)$$

简化后：

$$b_n=\frac{2}{\pi n}(1-\cos (n\pi ))$$

注意到$1-\cos (n\pi )=2$ 当n为奇数，0当 n 为偶数。

因此：

$$b_n=\{\begin{array}{ll}\frac{4}{\pi n},& n\text{ 是奇数}\\ 0,& n\text{ 是偶数}\end{array}$$

所以，函数的傅里叶级数为：

$$f(x)=\sum _{n=1,n\text{奇}}^{\infty }\frac{4}{\pi n}\sin (nx)$$

实验可视化

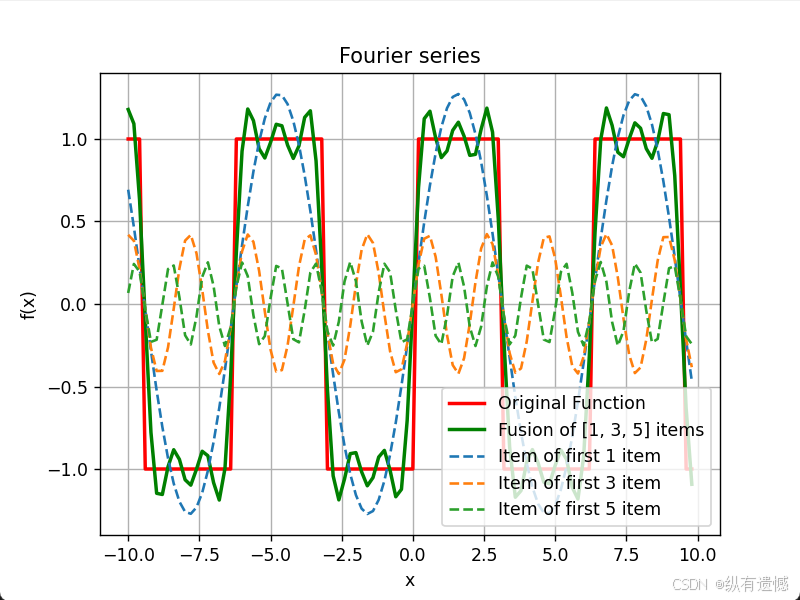
下面是具体的实验代码

# 安装依赖
pip install numpy matplotlib

import matplotlib.pyplot as plt
from math import pi
import numpy as np

def func_origin(x:float): # 原函数
    if x<pi and x>=0:
        return 1
    if x<2*pi and x>=pi:
        return -1
    x = x - (x//(2*pi))*2*pi
    return func_origin(x)

def func_sub_x(x:float, n:int): # 子函数
    coef = 4/(n*pi)
    return coef * np.sin(n*x)

def paint(x_data, y_data_origin, y_data_synthetic_arr, num_arr): # 绘图
    plt.plot(x_data, y_data_origin, label='Original Function', color='red', linewidth=2)
    plt.plot(x_data, np.sum(y_data_synthetic_arr, 0), label=f'Fusion of {str(num_arr)} items', color='green', linewidth=2)
    for i in range(len(num_arr)):
        y_data_synthetic, n = y_data_synthetic_arr[i], num_arr[i]
        plt.plot(x_data, y_data_synthetic, label=f'Item of first {n} item', linestyle='dashed')
    
    plt.legend()
    plt.xlabel('x')
    plt.ylabel('f(x)')
    plt.title('Fourier series')
    plt.grid(True)
    plt.show()

def main(num_arr):
    x = [i for i in np.arange(-10, 10, 0.2)]
    y_origin = [func_origin(e) for e in x]
    y_data_synthetic_arr = []
    for i in num_arr:
        item = [func_sub_x(e,i) for e in x]
        y_data_synthetic_arr.append(item)
    paint(x, y_origin, y_data_synthetic_arr, num_arr)

if __name__ == "__main__":
    main([1,3,5])