概述

梯度下降的自适应方法是标准梯度下降算法的变体，它根据数据的特征和优化过程调整学习率。自适应方法的目标是通过以更适合手头任务的方式扩展学习率来提高优化的收敛性。

介绍

梯度下降是一种广泛使用的优化算法，用于查找最小化成本函数的参数值。在机器学习中，梯度下降通常用于优化模型的参数以提高其性能。梯度下降背后的主要思想是通过遵循成本函数的负梯度来迭代改进参数的值。通过在降低成本函数的方向上采取小步骤，梯度下降可以有效地找到参数的最优值。梯度下降的几种变体，包括 AdaGrad、Adadelta、RMSprop、Adam 和 Nadam，使用不同的技术来调整学习率并提高优化的收敛性。本文将讨论梯度下降的这些变体，以及我们如何在机器学习应用程序中使用它们。

什么是梯度下降？

梯度下降是一种优化算法，用于通过沿梯度负数定义的最陡峭下降方向迭代移动来最小化某些函数。在机器学习中，它通常用于更新模型的参数以最小化误差/损失函数。几种算法变体（例如批量梯度下降、随机梯度下降和小批量梯度下降）在用于计算每次迭代时梯度的示例数量上有所不同。

问题：问题在于找到最佳系数一个一个和b对于函数f接受输入x和y并最小化成本函数J.

解决方案：使用梯度下降，我们从一些初始值开始，一个a和b，并通过遵循成本函数的负梯度来迭代改进这些值J。

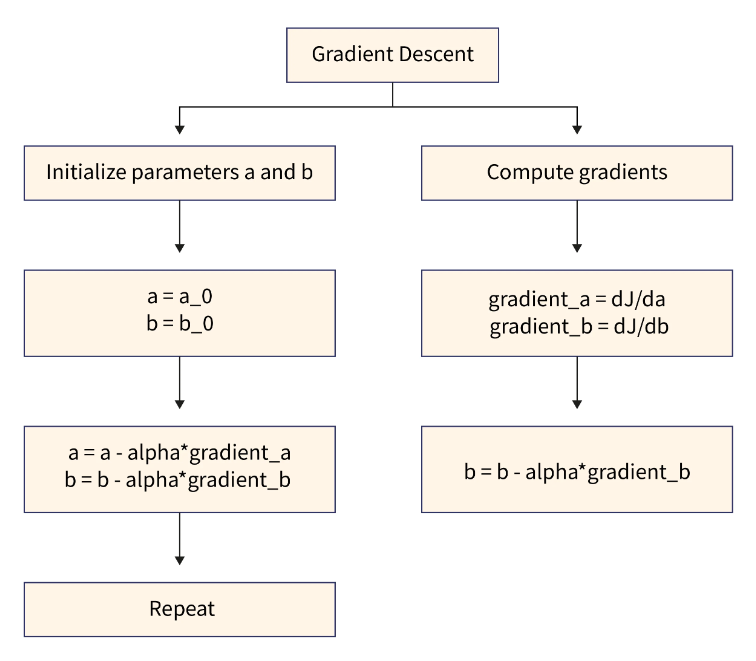
步骤：

• 计算有关参数的成本函数的梯度一个a和b
• 在降低成本函数的方向上更新参数
• 重复此过程，直到成本函数最小化

注意：学习率是一个超参数，它决定了更新参数所采取的步骤的大小。较大的学习率可能会超过最佳值，而较低的学习率会减慢该过程。

自适应梯度 （AdaGrad）

AdaGrad（自适应梯度）是梯度下降算法的一种变体，可单独调整每个参数的学习率。基本思想是，梯度高的参数学习率会更低，梯度低的参数学习率会更大。这允许算法更快地收敛稀疏数据。

在 Adagrad 算法中，学习率在每次迭代中更新，如下所示：

这里​和​分别是参数 a 和 b 的梯度平方和。这些值会随着时间推移而累积到每个参数。参数a，b通过梯度下降步长学习，学习率乘以归一化梯度。

归一化因子​和防止学习率变得太小，这可能会减慢算法的收敛速度并跟踪过去的梯度信息。

使用 AdaGrad 进行梯度下降

AdaGrad 对于处理稀疏数据和处理稀疏梯度特别有用。由于 AdaGrad 保持每个参数的学习速率，因此可以处理稀疏梯度，从而允许每个权重具有其学习速率，而不管数据的稀疏性如何。

二维测试问题

测试问题由函数 f(x) 定义，该函数接受二维输入x并返回输出(x[0]∗∗2) + (2∗x[1]∗∗2)。此函数的全局最小值为 x = [0, 0]。

import numpy as np

# Define the test function
def f(x):
    return x[0]**2 + 2*x[1]**2

使用 AdaGrad 进行梯度下降优化

优化算法从 x 的一些初始值开始，然后通过遵循成本函数的负梯度来迭代改进这些值，并使用梯度下降找到 x 的最优值，包括重复计算成本函数相对于 x 的梯度，并在降低成本函数的方向上更新 x。

在这种情况下，使用 grad_f（x） 函数计算成本函数的梯度，该函数返回梯度[(2∗[0]),(4∗[1])][(2∗x[0]), (4∗x[1])]. 学习率是一个超参数，用于确定更新 x 所采取的步骤的大小。在本例中，学习率设置为 0.1。

AdaGrad 根据参数调整学习率，对不频繁的参数执行较大的更新，对频繁的参数执行较小的更新。在 AdaGrad 中，学习率除以前几步梯度平方和的平方根，这意味着学习率随着梯度的增加而降低。

# Define the gradient of the test function
def grad_f(x):
    return np.array([2*x[0], 4*x[1]])

# Set the initial values of x
x = np.array([10, 10])

# Set the learning rate and the initial value of the sum of the squares of the gradients
learning_rate = 0.1
sum_squares_gradients = np.zeros_like(x)

# Perform gradient descent for a fixed number of iterations
for i in range(100):
    # Compute the gradient of the cost function
    gradient = grad_f(x)
    # Update the sum of the squares of the gradients
    sum_squares_gradients += (gradient**2).astype(sum_squares_gradients.dtype)



    # Update the parameters using AdaGrad
    x = x.astype(float)  # or x = x.astype(np.float64)
    x -= learning_rate * gradient / np.sqrt(sum_squares_gradients + 1e-7)




# Print the final values of the parameters
print(x)

输出

[8.20722233 8.20805769]

AdaGrad 的可视化

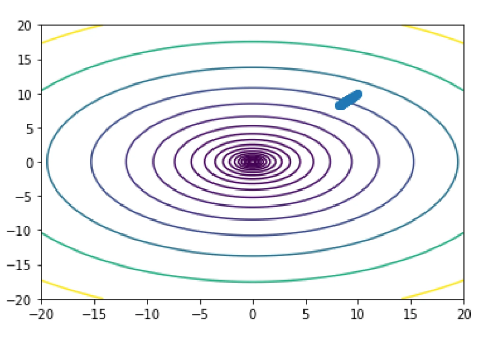
通过绘制成本函数和优化过程中参数的轨迹来可视化优化过程。 通过在点网格上计算函数f（x） 并使用等值线函数绘制成本函数的等值线来绘制成本函数。

参数的轨迹是通过在每次迭代中存储 x 的值并使用 plot 函数绘制 x 的路径来绘制的。 最后，使用 show 函数显示绘图。

import matplotlib.pyplot as plt

# Define a grid of points to evaluate the cost function
X, Y = np.meshgrid(np.linspace(-20, 20, 100), np.linspace(-20, 20, 100))
Z = f(np.array([X, Y]))

# Set the initial values of x
x = np.array([10, 10])

# Set the learning rate and the initial value of the sum of the squares of the gradients
learning_rate = 0.1
sum_squares_gradients = np.zeros_like(x)

# Initialize a list to store the values of x at each iteration
x_values = [x.copy()]

# Perform gradient descent for a fixed number of iterations
for i in range(100):
    # Compute the gradient of the cost function
    gradient = grad_f(x)
    # Update the sum of the squares of the gradients
    sum_squares_gradients += (gradient**2).astype(sum_squares_gradients.dtype)
    # Update the parameters using AdaGrad
    x = x.astype(float)  # or x = x.astype(np.float64)
    x -= learning_rate * gradient / np.sqrt(sum_squares_gradients + 1e-7)
    # Store the values of x at each iteration
    x_values.append(x.copy())

# Convert the list of x values to a numpy array
x_values = np.array(x_values)

# Plot the cost function
plt.contour(X, Y, Z, levels=np.logspace(-1, 3, 20))

# Plot the trajectory of the parameters
plt.plot(x_values[:, 0], x_values[:, 1], '-o')

# Show the plot
plt.show()

输出

Adadelta

Adadelta 是 Adagrad 的扩展，它通过基于梯度的移动平均线和平方梯度的移动平均线缩放学习率来降低 Adagrad 的积极、单调递减的学习率。Adadelta 不需要手动学习率，也可以处理可变长度序列。

公式： ​=时间 t 处的参数梯度

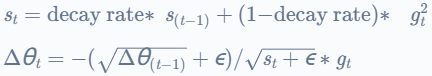
哪里衰减率衰减率是一个超参数，​是累积梯度，​是参数更新，ϵ是一个小常数，添加该常数以避免除以零，并且​是时间的梯度t.

RMSprop

RMSprop 是一种优化算法，它使用平方梯度的移动平均值来缩放学习率。RMSprop 将学习率除以梯度平方移动平均线的平方根，从而降低了大梯度的学习率，提高了小梯度的学习率。

公式：

​=时间 t 处的参数梯度

​ = 衰减率∗ ​+ (1−衰减率) ∗ ​

参数 −= 学习率 

其中衰减率是一个超参数，​是累积梯度，learning_rate 是全局学习率和ϵ是一个小常量，添加以避免除以零。

Adam

Adam（自适应矩估计）是一种优化算法，它使用梯度的移动平均线和平方梯度来缩放学习率。Adam 使用梯度的第一和第二时刻计算每个参数的学习率，并根据这些时刻的指数衰减调整学习率。Adam 已被证明适用于许多应用程序，被认为是最好的优化算法之一。

公式：

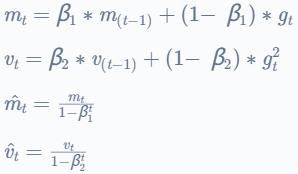
参数 −= 学习率 ∗ 

其中 beta1 和 beta2 是两个超参数，​和​是梯度的移动平均线，并且​是时间 t 的梯度。

Nadam

Nadam（Nesterov 加速自适应矩估计）是 Adam 的扩展，它使用 Nesterov 动量技术进一步加速优化收敛。Nadam 将 Nesterov 方法的动量与 Adam 的自适应学习率相结合，并已被证明在各种任务中表现良好。

公式：

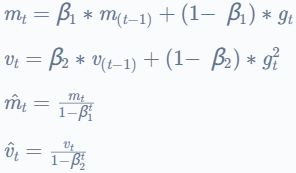
参数 = 学习率 ∗ 

其中 beta1 和 beta2 是两个超参数，​和​是梯度的移动平均线，​是时间t和learning_rate的梯度；epsilon和以前一样。

结论

• 梯度下降及其变体是提高机器学习模型性能的重要工具。
• 通过迭代找到参数的最优值，梯度下降可以帮助机器学习模型做出更准确的预测，并更好地泛化到新数据。
• 优化算法的选择会显著影响机器学习模型的性能，因此选择最适合手头任务的算法非常重要。
• 综上所述，梯度下降及其变体是机器学习中广泛使用的强大优化算法，可以成为提高机器学习模型性能的重要工具。